Reference
【概述】
评价指标可以说明模型的性能,辨别模型的结果,在建立一个模型后,计算指标,从指标获取反馈,再继续改进模型,直到达到理想的效果,因此,在预测之前检查模型的评估指标至关重要,不应在建立一个模型后,就直接将模型应用到看不见的数据上
对于分类问题来说,其根据所分类别的个数,可分为二分类问题、多分类问题
在二分类问题中,使用的评价指标有:误差率(Error Rate)、准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1 分数(F1 score)、$F_\beta$ 分数($F_\beta$ score)、PR 曲线、ROC 曲线、AUC、代价敏感错误率(Cost-sensitive Error Rate)、代价曲线(Cost Curve)等
在多分类问题中,使用的评价指标有: 宏精确率(macro-P)、宏召回率(macro-R)、宏 F1(macro-F1) 、微精确率(micro-P)、微召回率(micro-R)、微F1(micro-F1)等
本文将详细介绍代价敏感错误率(Cost-sensitive Error Rate)、代价曲线(Cost Curve)
【误分类代价与代价矩阵】
在 分类问题的评价指标(二) 中,简单提及了误分类代价 $C(-|+)$ 与 $C(+|-)$ ,下面将详细进行介绍
现实情况中,不同的错误造成的后果不同,为权衡不同错误造成的不同损失,为错误赋予非均等代价(Unequal Cost)
对于二分类问题,设定一个代价矩阵(Cost Matrix),用误分类代价 $C(j|i)$ 代表第 $i$ 类样本预测为第 $j$ 类样本的代价,且 $C(i|i)=0$,此处的代价是指的比值,即 5:1 与 50:10 的效果相当
若将第 $0$ 类判别为第 $1$ 类所造成的损失更大,则 $C(1|0)>C(0|1)$,损失程度相差越大,$C(1|0)$ 与 $C(0|1)$ 差别越大
如下图,设第 $0$ 类为负类,第 $1$ 类为正类,则 $cost_{01}$ 是负类样本被预测为正类样本的代价,$cost_{10}$ 是正类样本为预测为负类样本的代价
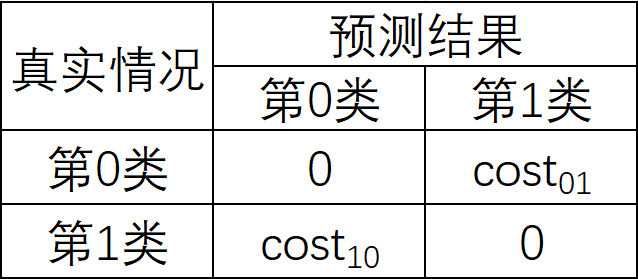
【代价敏感错误率】
在均等代价下,错误率大多都是直接计算错误次数,并没有考虑不同错误造成不同的后果,在非均等代价下,我们希望的不再是最小化错误次数,而是最小化总体代价(Total Cost)
对于样本容量为 $n$ 的测试集 $T$,若将第 $1$ 类作为正类,第 $0$ 类作为负类,令 $T^+$ 表示测试集的正类集,$T^-$ 表示测试集的负类集,对于学习到的模型为 $Y=f(X;\boldsymbol{\theta})$,代价敏感错误率(Cost-sensitive Error Rate)定义为:
此外,如果令 $C(j|i)$ 中 $i$、$j$ 的取值不仅限于 $0$、$1$,则可定义出多分类问题的代价敏感性能度量标准
【代价曲线】
ROC 曲线无法直接反应期望总体代价,为解决该问题,引入了代价曲线(Cost Curve)
均等代价下的代价曲线
在均等代价下,即 $C(-|+)=C(+|-)$ 时,此时期望代价就是错误率,且运行条件(Operating Condition)就是数据集中正类所占的比例 $p(+)$
我们希望用实际使用时的性能来评估分类器,但实际数据集中的正类所占比例 $p(+)$ 是未知的,因此应该得到所有可能的 $p(+)$ 值上的性能来对分类器进行评估
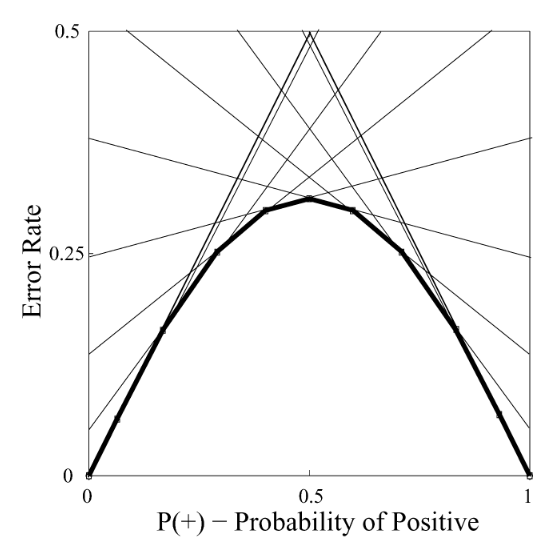
此时,绘制一个二维坐标系统,的 $x$ 轴是 $p(+)$,$y$ 轴是错误率,当 $x=0$ 时,意味着数据集中全是反例,一个分类器在该数据集上的整体错误率就等于将所有正例预测为反例的概率,即 FNR;当 $x=1$ 时,意味着数据集中全是正例,一个分类器在该数据集上的整体错误率就等于将反例预测为正例的概率,即 FPR
这样一来,在 ROC 空间中的一个分类器所对应的点,在该二维坐标系统中就成了一条线段,这个二维坐标系统中的所有线段所围成的下包络线,就是在误分类代价等价下的代价曲线
非均等代价下的代价曲线
下面从均等代价向非均等代价推广
在非均等代价下,即 $C(-|+)\neq C(+|-)$ 时,考虑所有可能的运行条件(Operating Condition),即考虑所有的 (类别分布,误分类代价)对,此时,一个分类器的期望代价为:
最大期望代价是在所有的样本都被错误分类,即 $FNR=FPR=1$ 时,此时有:
通过期望代价对最大期望代价进行归一化,有:
此时,归一化后的最大期望代价 $E_{Norm}(Cost)$,即非均等代价下的代价曲线的纵轴,其取值范围是 $[0,1]$
回过头来看 ROC 空间中的一个点 $(TPR,FPR)$,由于 $TPR=1-FNR$
那么,由于在均等代价下,ROC 空间与 CC 空间中的直线是一一对应的,可以视为不严格的对偶(Dual),那么在从均等代价向非均等代价推广过程中也应当极力保障这个性质,这样可以对模型的分析、评价带来极大的便捷
为了配合纵轴的归一化思路,只有对横轴进行同样的操作才可确保直线,即在数据集中正类所占的比例 $p(+)$ 的基础上引入包含误分类代价的信息,有:
之后再进行归一化:
此时,归一化后的引入误分类代价信息的在数据集中正类所占的比例 $PC(+)$,即非均等代价下的代价曲线的横轴,其取值范围是 $[0,1]$
类似的,还可定义 $PC(-)$,即:
由于 $p(+)=1-p(-)$,易得:
将上式带入归一化后的最大期望代价 $E_{Norm}(Cost)$,有:
将 $PC(+)\in[0,1]$ 整体看作自变量,至此,就得到了非等价代价下的代价曲线的线性参数方程,其绘制出的图形是一条左端点位于点 $(0,FPR)$,右端点位于点 $(1,FNR)$ 的线段
在非均等代价的 CC 空间中所有线段围成下包络线就是非均等代价的代价曲线
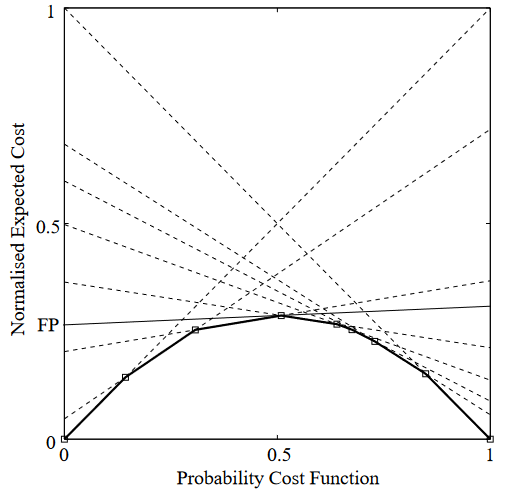
ROC 曲线与代价曲线的转换
ROC 曲线,它可视化的是 $FPR$(横轴) 和 $TPR$(纵轴)的关系,代价曲线则可视化了正例先验概率 $PC(+)$ 和最小代价期望 $E_{Norm}(Cost)$ 的关系
而 ROC 空间中的一个点是与 CC 空间中的一条线段存在着不严格的对偶关系,也就是说,ROC 曲线与代价曲线是可以互相转换的:一旦获得了 ROC 曲线的所有信息,就可以逐点画出另个坐标系里对应的线段;反之,如果有一条代价曲线,就可以通过画切线,看切线左右的截距来得到 $FPR$ 和 $FNR$,而 $TPR=1-FNR$,进而即可绘制出 ROC 曲线
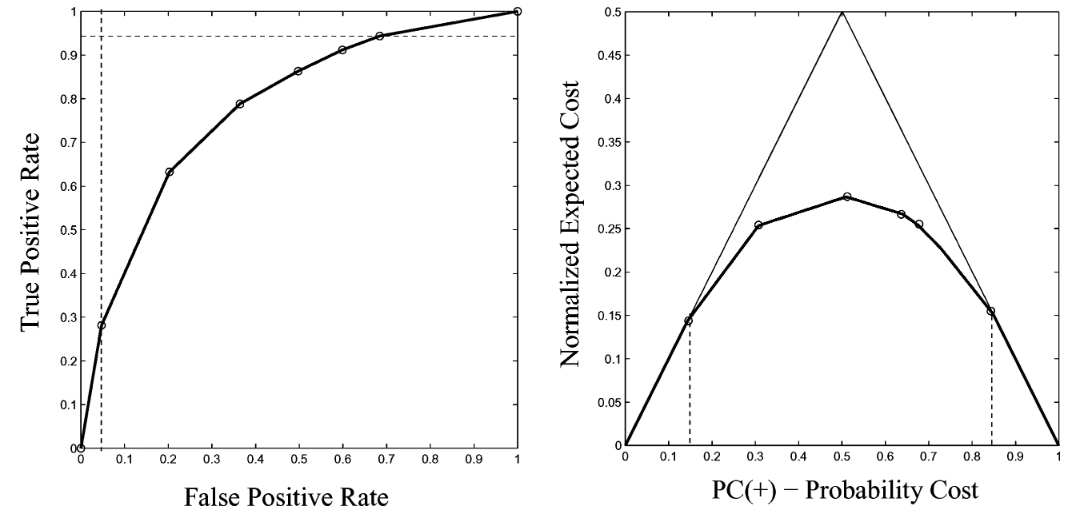
包络线下的面积
在 CC 空间中,任一直线的绘制均与代价无关,那么所有直线拟合出的下包络线即代价曲线,也与代价无关
简单来说,对于分类器,给定一个阈值,相应地统计出一个 $(FPR,FNR)$ 组合,再根据该组合绘制出一条直线,全程没有用到代价
对于已知的 $(FPR,FNR)$ 组合,其在 CC 空间中绘制出的单根线段与横轴间的梯形面积,即模型对于某一阈值的期望总体代价(期望总体错误率)
在代价曲线中,横轴是正例先验概率,即一个关于正例概率 $p$ 的函数,那么,利用积分的方法,即可求出这个梯形面积:
既然当给出一个 $(FPR,FNR)$ 组合时,任一直线的绘制与代价无关,那么所有直线拟出的下包络线即代价曲线,也与代价无关
同样,当给定一个正例概率 $p$ 的函数时,代价曲线下的面积即模型对于所有阈值的期望总体代价(期望总体错误率),也可通过积分的方式求出:
其中,$\Omega$ 是一个模型对应的所有 $(FNR,FPR)$ 的集合,即 CC 空间中所有线段的端点,寻找下确界 $\inf$ 的操作则对应了寻找下包络线