MP 神经元

【概述】

MP 神经元是由 McCulloch 与 Pitts 于 1943 年发表的神经元模型，其是按照生物神经元的结构与工作原理所构造的一个抽象与简单的模型，简单模拟了神经元的反应流程

在目前的神经网络中，最基本的单元就是神经元（Neuron），即 MP 神经元

而神经网络训练的过程，实际上就是根据训练样本调整 MP 神经元权重和阈值的过程

【生物神经元】

对于生物神经网络来说，可以概括出以下特点：

1. 每个神经元都是一个多输入单输出的信号处理单元
2. 神经元输入分为兴奋性输入、抑制性输入两种类型
3. 神经元具有空间整合特性与阈值特性
4. 神经元输入与输出间存在固定的时延，主要取决于突触延搁

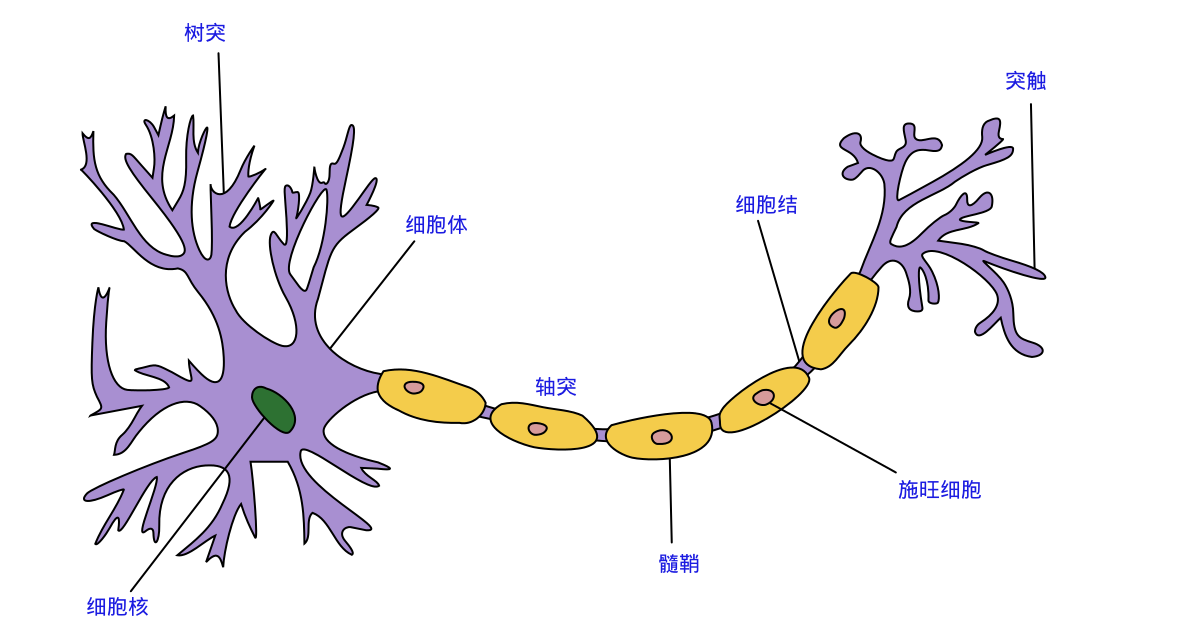
【MP 神经元结构】

上图展示了生物神经元的基本结构，仿照生物神经元的结构，忽略时间整合作用、不应期等复杂因素，同时将神经元突触时延与强度作为常数，可建立出如下图所示的 MP 神经元

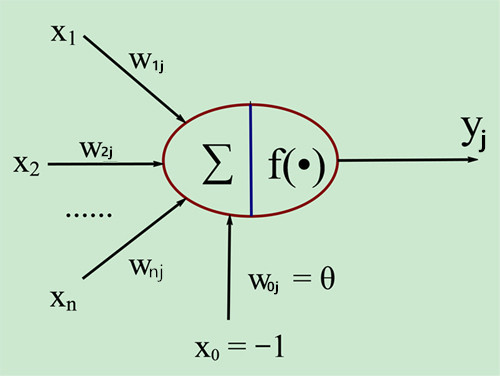
【从生物神经元到 MP 神经元】

下面，将生物神经元与 MP 神经元进行对比：

生物神经元	MP 神经元
神经元	$j$
输入信号	$x_i$
刺激的不同强度	$w_{ij}$
突触	$w_{ij}x_i$
汇聚电信号的细胞膜	$\sum$
膜电位	$\sum\limits_{i=1}^nw_{ij}x_i$
外界刺激达到什么程度神经元才会被激活	$\theta_j$
神经元被激活释放脉冲	$f(\cdot)$
输出信号	$y_j$

结合 MP 神经元的结构图来看，对于某个 MP 神经元 $j$ 来说，其可同时接收多个输入信号 $x_i$，代表外界刺激

由于生物神经元具有不同的突触性质与强度，用权值 $w_{ij}$ 表示，其正负模拟了生物神经元中的兴奋与抑制，其大小模拟了生物神经元中突触的不同连接强度，由此，输入信号 $x_i$ 与权值 $w_{ij}$ 模拟了生物神经元的突触部分

在生物神经元中，会将多个突触末梢的电信号在细胞膜中进行汇聚，在 MP 神经元中使用 $\sum$ 函数来代表，$\sum\limits_{i=1}^nw_{ij}x_i$ 就是将所有突触末端的刺激进行汇聚，将多个值合并为一个值，由此代表生物神经元汇聚后的膜电位

生物神经元只有在受到外界刺激一定程度后才会被激活，由此设置了阈值（Threshold）又称偏置（Bias） $\theta_j$，高于阈值电平的部分为整个神经元的净激活（Net Activation）值，即：

$$net_j=\sum_{i=1}^nw_{ij}x_i-\theta_j$$

考虑到只有当输入总和超过阈值时，神经元才会被激活释放脉冲，为此，使用 $f(\cdot)$ 来表示激活函数，用来确定是否产生神经元的输出

因此，整个 MP 神经元可用如下公式表达：

$$\begin{align*} y_j &= f(net_j)\\ &= f(\sum_{i=1}^nw_{ij}x_i-\theta_j) \end{align*}$$

【MP 神经元的表示】

对于 MP 神经元：

$$y_j=f(\sum_{i=1}^nw_{ij}x_i-\theta_j)$$

如果将阈值 $\theta_j$ 看作一个输入为 $x_0=-1$ 且连接权重为 $w_{0j}$ 的哑结点，那么权重 $w_{ij}$ 和与阈值 $\theta_j$ 可进行统一，即：

$$y_j=f(\sum_{i=0}^nw_{ij}x_i)$$

进一步，用 $X$ 表示输入向量，用 $W$ 表示权重向量，即：

$$\begin{matrix} X=[x_0,x_1,...,x_n],W=\begin{bmatrix} w_{0j} \\ w_{1j} \\ \vdots w_{nj} \end{bmatrix} \end{matrix}$$

则 MP 神经元的净激活为：

$$net_j=XW$$

则整个 MP 神经元可表示为：

$$y_j=f(XW)$$

若 $net_j>0$，则神经元处于兴奋状态，若 $net_j<0$，则神经元处于抑制状态