决策树的剪枝策略

【概述】

剪枝（Pruning）是决策树处理过拟合的主要手段，即通过主动去掉一些分支来降低过拟合的风险

决策树剪枝的基本策略有预剪枝（Pre-Pruning）、后剪枝（Post-Pruning）两种，在实际应用中，往往使用后剪枝策略更多一些

【预剪枝】

预剪枝是在决策树生成过程中进行的剪枝，其基于贪心策略，不仅可以降低过拟合的风险，而且还可以减少训练时间，但可能会出现欠拟合现象

预剪枝是在决策树生成过程中进行的剪枝，常用的方法有：

1. 提前设定决策树的高度，当达到这个高度时，停止构建决策树
2. 当达到某节点的实例具有相同的特征向量，停止树的生长
3. 提前设定阈值，当达到某个节点的样例个数小于该阈值的时，停止树的生长（该方法无法用于数据量较小的训练样例）
4. 提前设定阈值，每次扩展决策树后，计算其对系统性能的增益，若小于该阈值，则停止生长
5. 对每个结点在划分前进行估计，若当前结点的划分无法使决策树的泛化性能提升，则停止划分，并将当前结点标记为叶结点

【后剪枝】

后剪枝是在决策树生成之后，对于一棵完整的决策树，按照树的前序遍历或后序遍历的顺序，对分支结点进行考察，若分支结点对应的子树替换为叶结点能够带来决策树的泛化性能提升，则将子树替换为叶结点

目前主要应用的后剪枝方法有三种：

• 误差降低剪枝（Reduced Error Pruning，REP）
• 悲观错误剪枝（Pessimistic Error Pruning，PEP）
• 代价复杂度剪枝（Cost-Complexity Pruning，CCP）

此外，常见的后剪枝方法还有：基于错误的剪枝（Error-Based Pruning，EBP）、最小错误剪枝（Minimum Error Pruning，MEP）、临界值剪枝（Critical Value Pruning，CVP）、最优剪枝（Optimal Pruning，OPP）等，这里不再详细介绍

【误差降低剪枝】

剪枝策略

误差降低剪枝（Reduced Error Pruning，REP）是最简单粗暴的后剪枝方法，在利用训练样本生成决策树后，按照树的后序遍历算法，对于每个分支结点计算修剪前后在验证集上的分类错误率，来决定是否修剪该结点

算法流程如下：

1. 按照树的后序遍历顺序，依次决定 $n$ 个分支节点是否需要被修剪
2. 对于第 $i$ 个分支结点，假设要删除该分支结点的子树，使其成为叶结点，并赋予训练样本最常见的分类
3. 用验证样本计算修剪前、修剪后分类的错误率
4. 当修剪后的分类错误率小于等于修剪前的分类错误率时，删除该节点下的子树
5. 当 $i=n$ 时，终止算法，否则，令 $i=i+1$，执行步骤 2

误差降低剪枝使用了与训练集、测试集独立的验证集，验证集中的样本没有参与决策树的生成过程，一定程度上可以解决过拟合问题，但也可能会产生过剪枝的问题

实例

以下图为例，假设某训练集产生的决策树如下：

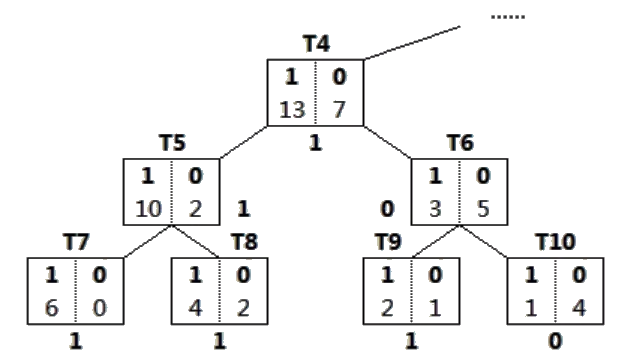
其中，T4 结点中 13 和 7 表示该节点覆盖的样本中目标变量为 1 和 0 的个数

假设用这个决策树拟合验证样本后的结果如下：

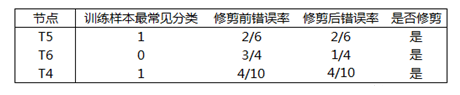
按照 T5、T6、T4 的顺序，计算修剪前后的错误率，依次决定每个节点是否需要被修剪：

【悲观错误剪枝】

剪枝策略

在 C4.5 中，所使用的剪枝策略，就是悲观错误剪枝（Pessimistic Error Pruning，PEP）策略

PEP 也是根据剪枝前后分类的错误率来决定是否剪枝，但与 REP 不同的是，PEP 不需要使用验证集，且 PEP 是按照树的前序遍历顺序剪枝的

设 $T$ 为考虑是否剪枝的分支结点，$t$ 为该结点下的叶结点，$N_t$ 表示叶结点 $t$ 覆盖的样本个数，$e_t$ 表示叶结点 $t$ 的错误分类样本个数，那么分支结点 $T$ 的分类错误率为：

$$E(T_t)=\frac{\sum_{t\in T}(e_t+\frac{1}{2})}{N_T}$$

其中，$\frac{1}{2}$ 是经验性惩罚因子，这是因为生成决策树与剪枝时使用的是相同的训练样本，那么对于每个结点，剪枝后分类错误率一定是会上升的，故而在计算分类错误率时，每个结点都要加上一个惩罚因子

对于分类错误率 $E(T_t)$，其含义是：每一个样本有 $E(T_t)$ 的概率分类错误，$1- E(T_t)$ 的概率分类正确，可以认为分类错误的次数服从伯努利分布，其误判次数为：

$$E(T_t)\cdot N_T$$

标准差为：

$$\sqrt{N_T\cdot E(T_t)\cdot (1-E(T_t))}$$

如果对分支结点 $T$ 进行剪枝，当 $T$ 成为叶结点后的分类错误率为：

$$E(T)=\frac{e_T+\frac{1}{2}}{N_T}$$

一般规定，当子树的误判次数大于对应叶节点的误判个数时，就决定剪枝，即满足下式就进行剪枝：

$$E(T_t)\cdot N_T+\sqrt{N_T\cdot E(T_t)\cdot (1-E(T_t))}\geq E(T)\cdot N_T$$

悲观错误剪枝的准确度较高，且不需要分离训练样本和验证样本，对样本量较少的情况比较有利

同时，每棵子树最多只需要访问一次，效率较高，但是由于方向是树的前序遍历方向，可能会造成某些不必要的剪枝

实例

以误差降低剪枝中的例子为例

考虑 T4 结点其错误分类样本个数，有：

$$e(T_4)=7$$

对于其叶结点的错误分类样本个数，有：

$$e(T_7)=0,e(T_8)=2,e(T_9)=1,e(T_{10})=1$$

则错误率为：

$$E(T_t)=\frac{(0+2+1+1)+4\cdot\frac{1}{2}}{20}=0.3$$

标准差：

$$S_e=\sqrt{(20\cdot 0.3\cdot(1-0.3)}=2.05$$

当 $T$ 成为叶结点后的分类错误率为：

$$E(T)=\frac{7}{20}$$

根据悲观错误剪枝的判断式：

$$E(T_t)\cdot N_T+\sqrt{N_T\cdot E(T_t)\cdot (1-E(T_t))}\geq E(T)\cdot N_T$$

有：

$$0.3\cdot20+2.05\geq \frac{7}{20}\cdot20$$

因此根据结点 T4 需要剪枝

【代价复杂度剪枝】

概述

在 CART 中，所使用的剪枝策略，就是代价复杂度剪枝（Cost-Complexity Pruning，CCP）策略，其按照树的后序遍历顺序从生成算法产生的决策树底端开始剪枝，根据剪枝的顺序，得到一系列的剪枝树 $\{T_0, T_1, T_2,…, T_m\}$，其中 $T_0$ 为原始决策树，$T_m$ 为根结点，$T_{i+1}$ 为 $T_i$ 剪枝后的结果，然后通过交叉验证法在独立的验证集上对剪枝树序列进行测试，从中选择最优子树

代价函数

对于任意子树 $T$，其叶结点个数为 $|T|$，取代价复杂度参数 $\alpha\geq 0$ ，树 $T$ 的代价函数定义为：

$$C_{\alpha}(T) = C(T)+\alpha|T|$$

在上述公式中，$C(T)$ 表示对训练数据的预测误差，用于表示模型与训练数据的拟合程度；$|T|$ 表示模型复杂度，即子树的叶结点个数；$\alpha$ 为代价复杂度参数，用于权衡训练数据的拟合程度和模型复杂度

对于固定的 $\alpha$，一点存在使代价函数 $C_a(T)$ 最小的子树 $T_{\alpha}$，$T_{\alpha}$ 在代价函数 $C_{\alpha}$ 最小的意义下是最优的，因此，剪枝就是在代价复杂度参数 $\alpha$ 确定时，选择代价函数最小的模型

对于代价复杂度参数 $\alpha$ 来说，$\alpha$ 越大，最优子树 $T_{\alpha}$ 就越小；$\alpha$ 越小，最优子树 $\alpha$ 就越大；在极端情况下，当 $\alpha=0$ 时，仅考虑模型与训练数据的拟合程度 $C_T$，不考虑模型的复杂度 $|T|$，此时整体树是最优的；当 $\alpha\rightarrow\infty$ 时，不考虑模型与训练数据的拟合程度 $C_T$，仅考虑模型的复杂度 $|T|$，此时由根结点组成的单结点树是最优的

代价复杂度参数

下面给出代价复杂度参数 $\alpha$ 的定义：

设 $T$ 为考虑是否剪枝的分支结点，$t$ 为该结点下的叶结点，$e_T$ 表示结点 $T$ 的分类错误率，$p_T$ 表示 $T$ 结点所覆盖的样本数占总样本数的比例，$|T_t|$ 表示 $T$ 结点下叶结点的个数

那么，对于结点 $T$ 下错误分类的样本个数占总样本个数的比例为：

$$R(T)=e_T\cdot p_T$$

对于结点 $T$ 下的所有叶结点 $t$，错误分类的样本个数占总样本个数的比例为：

$$R(T_t)=\sum_{t\in T}e_t\cdot p_t$$

则，代价复杂度参数定义为：

$$\alpha=\frac{R(T)-R(T_t)}{T_t-1}$$

同样以误差降低剪枝中的例子为例，给出代价复杂度参数 $\alpha$ 的计算实例

假设总样本数为 $60$，考虑 T4 结点，有：

$$R(T)=\frac{7}{20}\cdot \frac{20}{60}=\frac{7}{60}$$

对于 T4 结点之下的所有叶结点，有：

$$R(T_t)=\frac{0}{6}\cdot\frac{6}{60}+\frac{2}{6}\cdot\frac{6}{60}+\frac{1}{3}\cdot\frac{3}{60}+\frac{1}{5}\cdot\frac{5}{60}=\frac{4}{60}$$

此时，代价复杂度参数为：

$$\alpha=\frac{\frac{7}{60}-\frac{4}{60}}{4-1}=\frac{1}{60}$$

子树序列的生成

在有了代价函数和代价复杂度参数后，开始循环地对子树进行剪枝，算法流程如下：

输入：CART 生成的决策树 $T_0$

输出：决策树子树序列 $\{T_1,T_2,…,T_m\}$

1. 令 $k=0$，$T=T_0$，$\alpha=+\infty$
2. 按照树的后序遍历的顺序，计算子树 $T$ 的所有分支结点 $T_t$ 的代价复杂度参数 $\alpha$
3. 选择最小的代价复杂度参数 $\alpha_{min}$ 所对应的分支结点 $T_{min}$ 进行剪枝，得到子树 $T$（若多个分支结点具有相同最小的代价复杂度参数，则选择结点数最多的分支结点进行剪枝）
4. 令 $k=k+1$，$\alpha_k=\alpha_{min}$，$T_k=T$
5. 若 $T_k$ 不是由根结点及两个叶结点构成的树，则返回步骤 2，继续进行剪枝，否则令 $T_k=T_m$

选取最优决策树

对于剪枝得到的决策树子树序列 $\{T_1,T_2,…,T_m\}$，利用独立的验证集，测试子树序列中各子树的基尼指数

具有最小基尼指数的决策树，即最优决策树