线性可分与几何间隔

【线性可分与分离超平面】

在二维空间上，两类点被一条直线完全分开称为线性可分

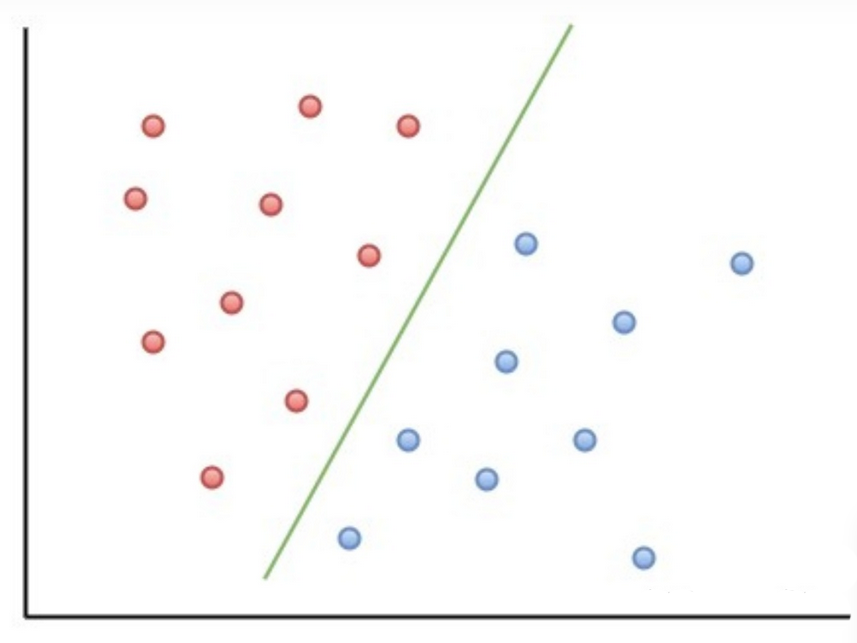
从二维空间扩展到多维空间中，其数学定义为：

对于 $n$ 维欧氏空间中的两个点集 $D_0$ 和 $D_1$，若存在 $n$ 维向量 $\boldsymbol{\omega}$ 和实数 $\theta$，使得所有属于 $D_0$ 的点 $\mathbf{x}_i$ 都有 $\boldsymbol{\omega}\cdot\mathbf{x}_i+\theta>0$，所有属于 $D_1$ 的点 $\mathbf{x}_j$ 都有 $\boldsymbol{\omega}\cdot\mathbf{x}_j+\theta<0$，则称 $D_0$ 和 $D_1$ 线性可分（Linearly Separable），否则称为线性不可分（Linearly Inseparable）

此时，线性方程 $\boldsymbol{\omega}\cdot\mathbf{x}_i+\theta=0$ 构成一个将点集 $D_0$ 和 $D_1$ 完全正确划分的分离超平面（Separating Hyperplane），其中，权值 $\boldsymbol{\omega}$ 为分离超平面的法向量，偏置 $\theta$ 是分离超平面的截距

【线性可分数据集】

对于给定的容量为 $n$ 的样本集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^n$，输出 $y_i\in\mathcal{Y}=\{+1,-1\}$

若存在某个分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 能够将训练集的正样本点与负样本点完全正确地划分到分离超平面的两侧，即：

• 对于所有的 $y_i=+1$ 的样本，有：$\boldsymbol{\omega}\cdot\mathbf{x}_i+\theta>0$
• 对于所有的 $y_i=-1$ 的样本，有：$\boldsymbol{\omega}\cdot\mathbf{x}_i+\theta<0$

则称训练集 $D$ 是线性可分的数据集，否则，称训练集 $D$ 为线性不可分的数据集

【函数间隔与几何间隔】

函数间隔

一般来说，一个点与分离超平面的距离，可以表示分类预测的确信程度

在分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 确定的情况下，$|\boldsymbol{\omega}\cdot\mathbf{x}_0+\theta|$ 表示输入空间 $\mathbb{R}^n$ 中任意一点 $\mathbf{x}_0$ 到超平面 $S$ 的距离，此时，通过判断 $\boldsymbol{\omega}\cdot\mathbf{x}_0+\theta$ 的符号与类标记 $y_0$ 的符号是否一致，即可表示分类是否正确

为此，定义函数间隔（Functional Margin），来表示分类预测的正确性以及确信度

对于给定容量为 $n$ 的样本集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(n)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}=\{+1,-1\}$

则分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 关于样本点 $(\mathbf{x}_i,y_i)$ 的函数间隔定义为：

$$\hat{\gamma_i} = y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)$$

那么分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 关于样本集 $D$ 的中所有样本点的函数间隔的最小值为：

$$\hat{\gamma} = \min_{i=1,2,\cdots,n} \hat{\gamma}_i$$

几何间隔

在选择分离超平面时，只有函数间隔还不够，因为只要成比例的改变 $\boldsymbol{\omega}$ 和 $\theta$，函数间隔也会成比例的改变（此时超平面不变），例如，将 $\boldsymbol{\omega}$ 和 $\theta$ 改为 $2\boldsymbol{\omega}$ 和 $2\theta$，此时函数间隔 $\hat{\gamma}_i$ 也变为原来的两倍

为此，可以使用 $L2$ 范数对分离超平面 $S$ 的法向量 $\boldsymbol{\omega}$ 进行约束，此时函数间隔就成了几何间隔（Geometric Margin）

对于给定容量为 $n$ 的样本集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(n)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}=\{+1,-1\}$

则分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 关于样本点 $(\mathbf{x}_i,y_i)$ 的几何间隔定义为：

$$\gamma_i = y_i \big( \frac{1}{||\boldsymbol{\omega}||_2}(\boldsymbol{\omega}\cdot\mathbf{x}_i+\theta) \big)$$

那么分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 关于样本集 $D$ 的中所有样本点的几何间隔的最小值为：

$$\gamma = \min_{i=1,2,\cdots,n} \hat{\gamma}_i$$

此时，分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 关于样本点 $(\mathbf{x}_i,y_i)$ 的几何间隔就是样本点到分离超平面的带符号的距离，当样本点被分离超平面正确分类时，就是样本点到分离超平面的距离

如图所示，$\boldsymbol{\omega}$ 为分离超平面的法向量，对于样本 $A$，$\gamma_i$ 为其到分离超平面 $S$ 的几何间隔

函数间隔与几何间隔的关系

分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 关于样本点 $(\mathbf{x}_i,y_i)$ 的函数间隔为：

$$\hat{\gamma_i} = y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)$$

分离超平面 $S:\boldsymbol{\omega}\cdot\mathbf{x}+\theta=0$ 关于样本点 $(\mathbf{x}_i,y_i)$ 的几何间隔为：

$$\gamma_i = y_i \big( \frac{1}{||\boldsymbol{\omega}||_2}(\boldsymbol{\omega}\cdot\mathbf{x}_i+\theta) \big)$$

两者有如下的关系：

$$\begin{align*} \gamma_i &= \frac{1}{||\boldsymbol{\omega}||_2} \hat{\gamma_i} \\ \gamma &= \frac{1}{||\boldsymbol{\omega}||_2} \hat{\gamma} \end{align*}$$

当法向量 $\boldsymbol{\omega}$ 的 $L2$ 范数为 $1$，即 $||\boldsymbol{\omega}||_2=1$ 时，函数间隔与几何间隔相等

同时，对于法向量 $\boldsymbol{\omega}$ 和截距 $\theta$ 成比例改变时，函数间隔也按该比例进行改变，但几何间隔不变