KD 树

【概述】

在实现 K 近邻时，主要考虑的是如何对训练数据进行 K 近邻搜索，最简单的实现方式是线性扫描（Linear Scan），此时要计算输入样本与每一个训练样本的距离，这在维度大的特征空间以及大容量的训练数据集中非常耗时

为提高 K 近邻搜索的效率，可以使用特殊的数据结构来存储训练数据，通过以空间换时间来快速查询样本的近邻

KD 树（K-Dimensional Tree）利用树结构在 $k$ 维空间上为数据集建立索引，其建立思想如同分治法，即利用已有数据对 $k$ 维空间进行切分

具体来说，KD 树表示了对 $k$ 维空间的一个划分（Partition），构造 KD 树相当于不断利用垂直于坐标轴的超平面将 $k$ 维空间切分，从而构成一系列的 $k$ 维超矩形区域，这样一来，树上的每一个点都对应于一个 $k$ 维超矩形区域

同时，由于 KD 树是二叉树结构，其时间复杂度上是 $O(\log n)$，相较于线性扫描的 $O(n)$ 的复杂度，有了极大的提高

此外，若在使用 sklearn 的 KNeighborsClassifier() 方法时，想利用 KD 树作为数据结构，在该方法参数中加入 algorithm='kd_tree' 即可

model = KNeighborsClassifier(n_neighbors=k, p=2, metric='minkowski', algorithm='kd_tree')

【KD 树的构造】

基本思想

构造 KD 树的基本思想是如下：先构造根结点，使根结点对应于 $k$ 维空间中包含所有样本的超矩形区域，之后对 $k$ 维空间进行递归切分，以生成子结点，每个子结点对应一个切分后的子超矩形区域，直到子区域内没有样本时终止切分，在迭代过程中，样本将被保存到相应的结点上

递归切分的方法是在超矩形区域上选择一个坐标轴，并在坐标轴上选择一个切分点，通过切分点来确定一个超平面，这个超平面通过选定的切分点，同时垂直于选定的坐标轴，此时，当前超矩形区域被切分为左右两个子超矩形区域

通常，依次选择坐标轴对空间进行切分，选择训练样本点在选定的坐标轴上的中位数作为切分点，此时得到的 KD 树，是一个平衡二叉树

算法流程

对于给定的数据集 $T=\{\mathbf{x_1},\mathbf{x_2},…,\mathbf{x_n}\}$，第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x_i} =(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$

构造 KD 树的算法流程如下：

Step 1：构造根结点，其对应于包含 $T$ 的样本输入 $\mathbf{x_i}$ 的 $m$ 维空间的超矩形区域，并进行切分，切分由通过切分点且与坐标轴 $x^{(1)}$ 垂直的超平面实现

1）选择 $x^{(1)}$ 作为切分的坐标轴，以 $T$ 中所有实例的 $x^{(1)}$ 坐标的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域

2）对于由根结点生成的深度为 $1$ 的左、右子结点：左子结点对应坐标 $x^{(1)}$ 小于切分点的子区域，右子结点对应坐标 $x^{(1)}$ 大于切分点的子区域

3）将落在切分超平面上的实例点，保存在根结点

Step 2：对于深度为 $j$ 的结点，进行迭代切分，切分由通过切分点且与坐标轴 $x^{(l)}$ 垂直的超平面实现

1）选择 $x^{(l)}$ 作为切分的坐标轴，$l=j\:(mod\:\:k)+1$，以该结点的区域中的所有实例 $x^{(l)}$ 坐标的中位数为切分点，将该结点对应的超矩形区域切分为两个子区域

2）对于由该结点生成的深度为 $j+1$ 的左、右子结点：左子结点对应坐标 $x^{(l)}$ 小于切分点的子区域，右子结点对应坐标 $x^{(l)}$ 大于切分点的子区域

3）将落在切分超平面上的实例点，保存在该结点

Step 3：重复 Step 2，直到两个子区域没有实例存在时停止，此时即形成 KD 树的区域划分

实例

给定一个输入 $\mathbf{x}$ 为二维的数据集 $T=\{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\}$

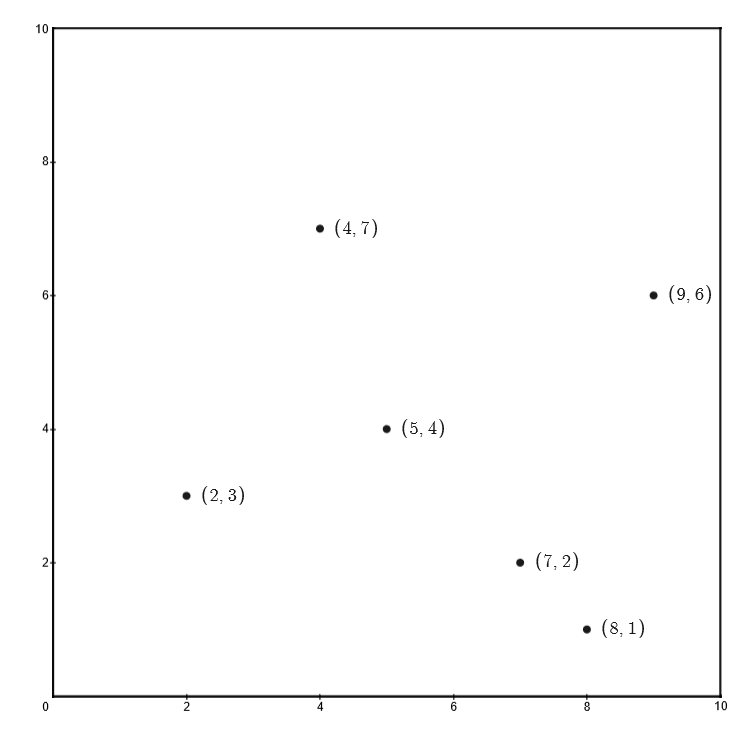
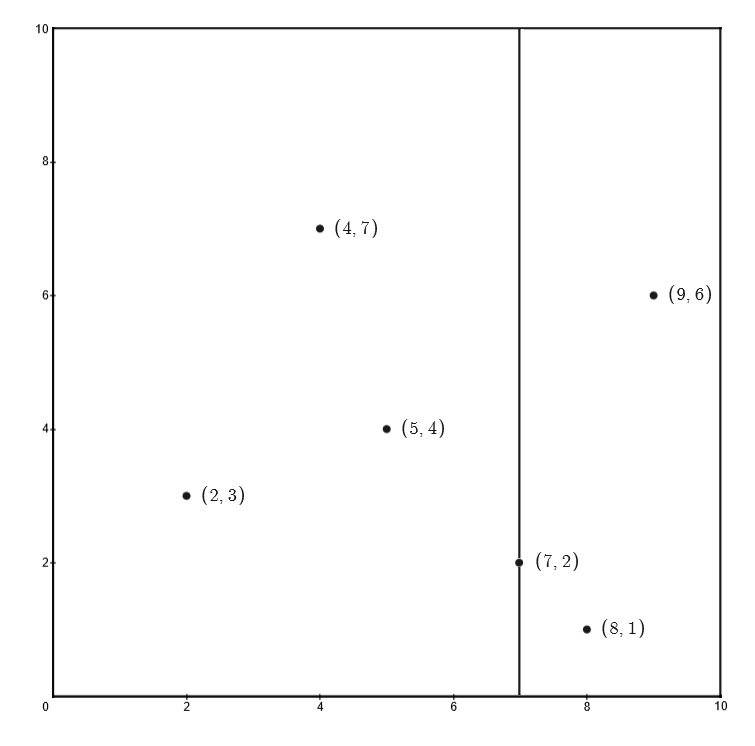
首先构造根结点，选择 $x^{(1)}$ 轴，$6$ 个数据点的 $x^{(1)}$ 坐标的中位数为：$7$，此时以平面 $x^{(1)}=7$ 将空间划分为左、右两个子矩形

接着，左矩形以 $x^{(2)}=4$ 划分为两个子矩形，右矩形以 $x^{(2)}=6$ 划分为两个子矩形

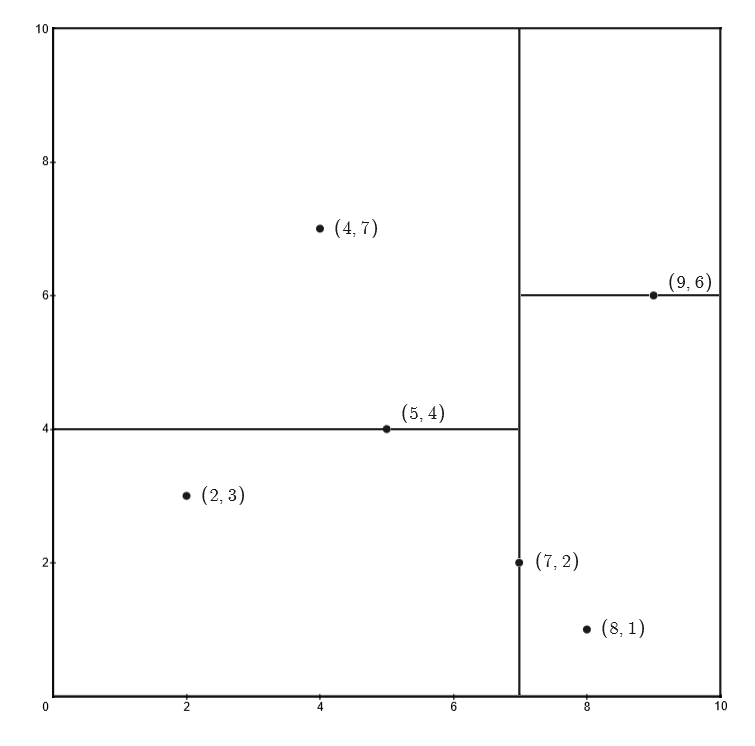
之后，对划分出的 $4$ 个子矩形递归的进行划分，对于左上矩形，以 $x^{(1)}=4$ 划分为两个子矩形；对于左下矩形，以 $x^{(1)}=2$ 划分为两个子矩形；对于右下矩形，以 $x^{(1)}=8$ 划分为两个子矩形

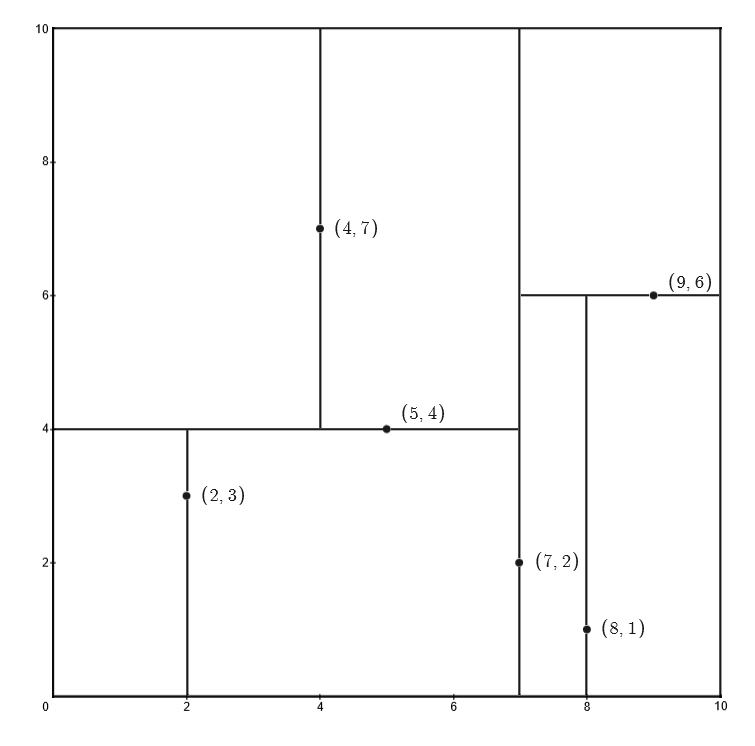
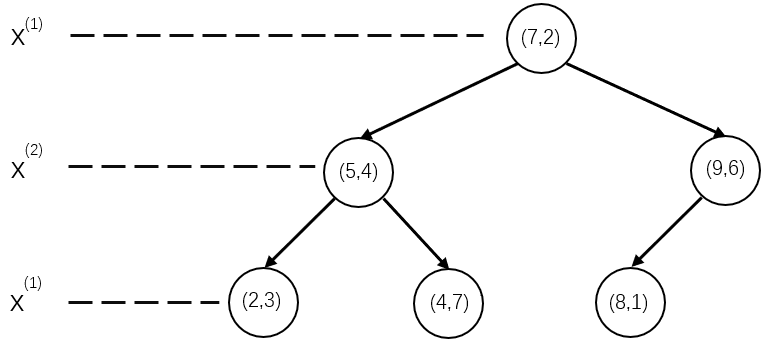
此时，特征空间划分完毕，根据特征空间划分可生成如下图所示的 KD 树

【KD 树的搜索】

基本思想

对于指定目标点，在 KD 树上寻找该目标点的最近邻时，其基本思想是：找到包含目标点的叶结点，然后从该叶结点出发，依次退回到父结点，在退回的过程中，不断查找与目标点最近邻的结点，当确定不可能存在更近的结点时终止

在上述过程中，包含目标点的叶结点对应包含目标点的最小超矩形区域，故而以该叶结点的样本点作为当前最近点，同时，目标点的最近邻一定是以目标点为中心，并且通过当前最近点的超球体内部

在返回当前结点的父结点时，若父结点的另一子结点的超矩形区域与超球体相交，那么就在相交的区域内寻找与目标点更近的样本点，若存在更近的样本点，就将该结点作为新的当前最近点，之后转到更上一级的父结点，重复上述过程

在返回当前结点的父结点时，若父结点的另一子结点的超矩形区域与超球体不相交，或不存在比当前点更近的点，则停止搜索

这样搜索就被限制在空间的局部区域上，效率得到极大的提高

算法流程

对于给定的数据集 $T=\{\mathbf{x_1},\mathbf{x_2},…,\mathbf{x_n}\}$，第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x_i} =(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，在构造完 KD 树后，求目标点 $\mathbf{x}$ 的最近邻的算法流程如下：

Step 1：从 KD 树的根结点出发，按如下步骤递归地寻找包含目标点 $\mathbf{x}$ 的叶结点

1）若目标点 $\mathbf{x}$ 当前维的坐标小于切分点的坐标，移动到左子结点

2）若目标点 $\mathbf{x}$ 当前维的坐标大于切分点的坐标，移动到右子结点

3）直到子结点为叶结点停止

Step 2：以 Step 1 中寻找到的叶结点为当前最近点

Step 3：按如下步骤递归地从叶结点向上回溯，对每个结点进行以下操作：

1）若该结点保存的样本点比当前最近点距离目标点更近，将该样本点作为当前最近点

2）当前最近点一定存在于该结点的某个子结点所对应的区域，检查该子结点的兄弟结点对应的区域是否有更近的点

a）该区域是否与以目标点为球心、以目标点与当前最近点的距离为半径的超球体相交

b）若相交，可能在该兄弟结点对应的区域内存在距目标点更近的点，移动到该兄弟结点中，接着向上递归

Step 4：当回溯到根结点时，搜索结束，最后的当前最近点，即为 $\mathbf{x}$ 的最近邻点

实例

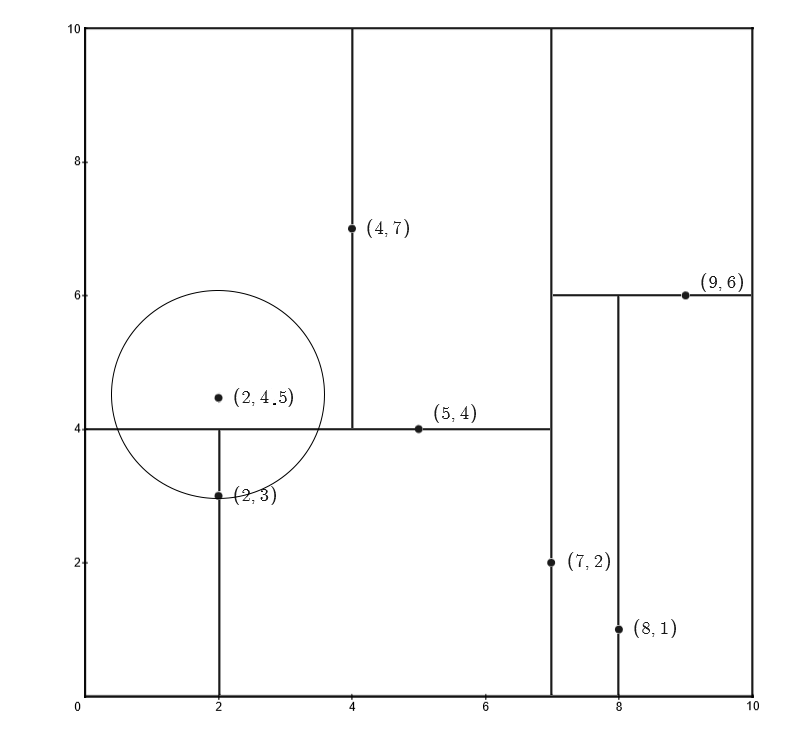
以下例所示的 KD 树为例，假设求输入的目标点 $(2,4.5)$ 的最近邻

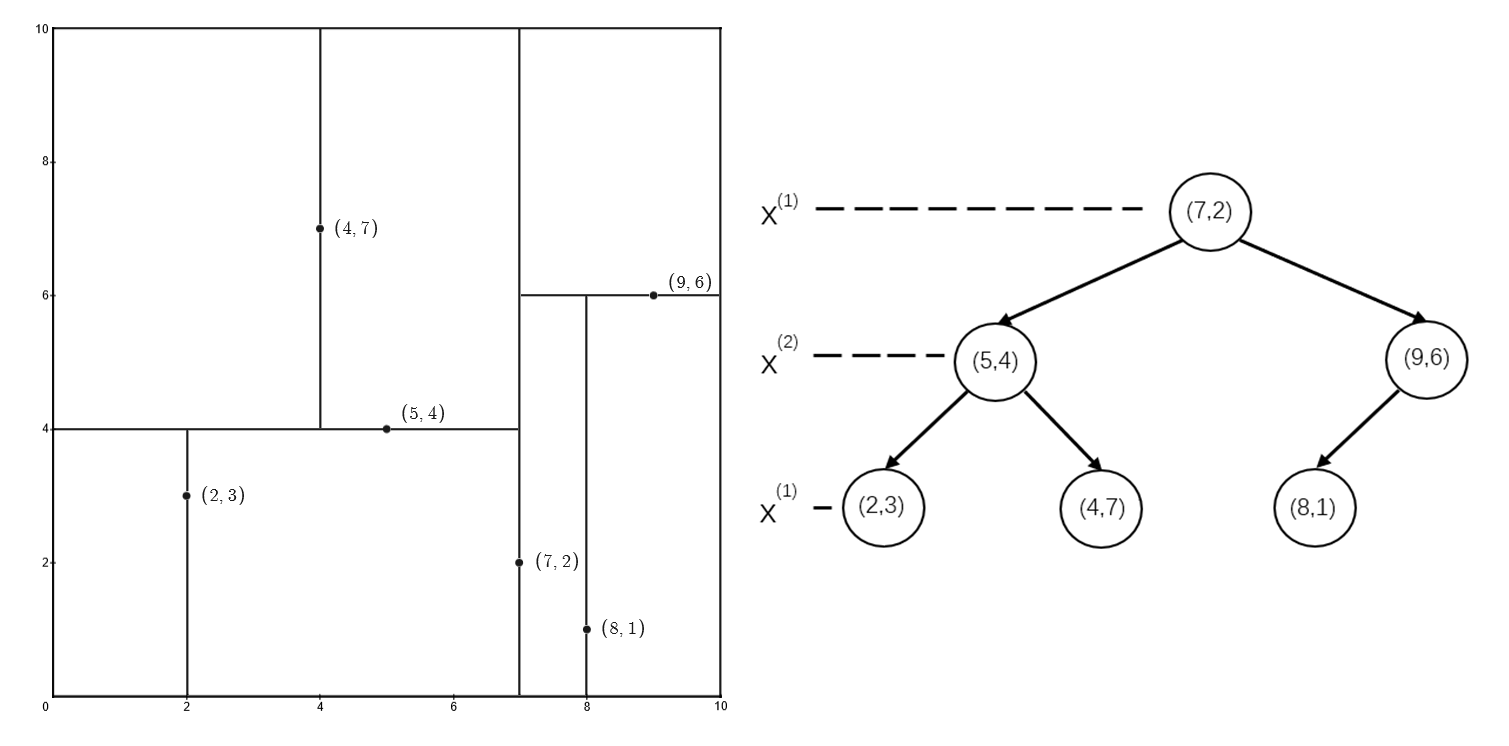
对于输入的目标点 $(2,4.5)$ 其落于叶结点 $(4,7)$ 上，将 $(4,7)$ 作为最近邻点，计算到该样本点的欧式距离，并将其作为最近距离，即：

$$d_{min}=\sqrt{(2-4)^2+(4.5-7)^2} \approx 3.2$$

在从叶结点向上回溯时，路径为：$(4,7)\rightarrow(5,4)\rightarrow(7,2)$

输入样本点 $(2,4.5)$ 与 $(4,7)$ 的父结点 $(5,4)$ 的欧式距离为：

$$d=\sqrt{(2-5)^2+(4.5-4)^2} \approx 3.04$$

该距离小于 $d_{min}=3.2$，这就意味着叶结点 $(4,7)$ 作为最近邻点不成立，此时更新最近距离为 $d_{min}=3.04$，同时以 $(5,4)$ 作为最近邻点

之后，以输入样本点 $(2,4.5)$ 为圆心，以 $d_{min}=3.04$ 为半径做圆

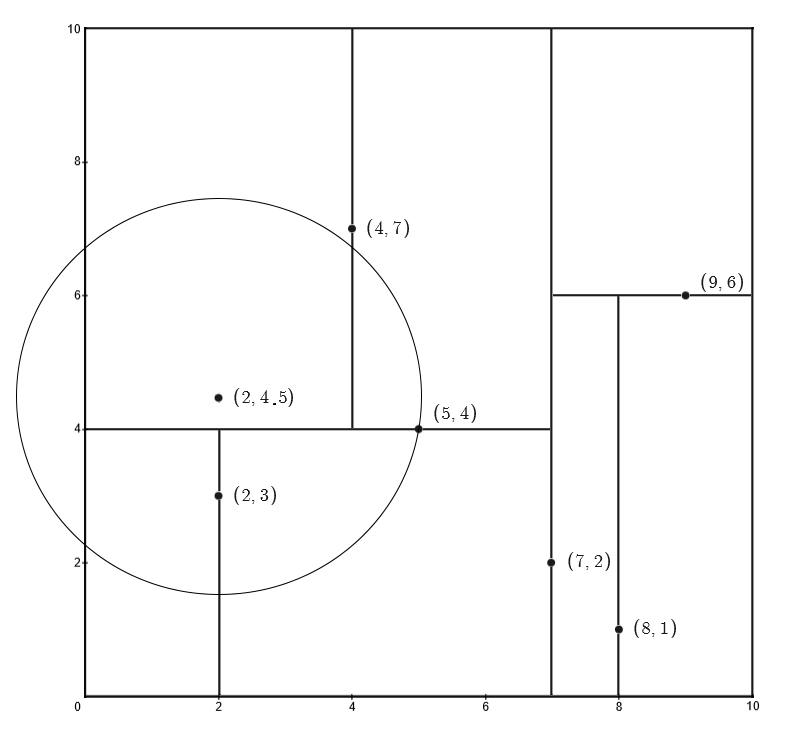
圆跟 $(5,4)$ 所切分的两个子区域相交，因此需要检查 $(5,4)$ 的另外一个子树的叶结点 $(2,3)$

输入样本点 $(2,4.5)$ 与叶结点 $(2,3)$ 的欧式距离为：

$$d=\sqrt{(2-2)^2+(4.5-3)^2} \approx 1.5$$

该距离小于 $d_{min}=3.04$，更新最近距离 $d_{min}=1.5$，并令 $(2,3)$ 为最近邻点

之后，回溯到根结点 $(7，2)$，由上图可以确认 $(7,2)$ 与切分的右子区域无关，回溯结束，$(2,3)$ 为最近邻点