Alex_McAvoy

想要成为渔夫的猎手

K 近邻

发表于 分类于 ， ，
本文字数： 8.2k 阅读时长 ≈ 7 分钟

【概述】

K 近邻（K-Nearest Neighbor，KNN）是常用的监督学习方法之一，既可处理分类问题，也可处理回归问题

一般来说，当利用 KNN 处理分类任务时，通常使用投票法，即选择这 $k$ 个邻居中出现最多的类别标记作为预测结果；当利用 KNN 处理回归任务时，通常使用平均法，即将这 $k$ 个邻居的输出标记的平均值作为预测结果

同时，KNN 是懒惰学习（Lazy Learning）的著名代表，在训练阶段仅仅将样本保存，训练开销时间为 0，待接收到测试样本后再进行处理；相应地，在训练阶段就对样本进行处理的学习方法，称为急切学习（Eager Learning）

KNN 需要计算待测样本和训练集中所有样本的距离，时间复杂度为 $O(n)$，一般适用于样本数较少的数据集，当数据集很大时，不仅耗时，而且需要大量的存储空间，因此当数据量大时，一般将数据以树的形式呈现，以提高速度，常用的方法有：KD-Tree 与 Ball-Tree

其中，KD 树对于低维度（$D<20$）的近邻搜索非常快，但当维数 $D$ 增长到很大时，效率会变低，这是维度灾难的一种体现，为解决 KD 树在高维上效率低下的问题，Ball 树应运而生

【算法流程】

虽然 KNN 既可处理分类问题，也可处理回归问题，但一般将其用于处理分类问题

就分类效果来说，KNN 对于随机分布的数据集分类效果较差，对于类内间距小，类间间距大的数据集分类效果好，且对于边界不规则的数据效果好于线性分类器

此外，KNN 对于样本不均衡的数据效果不好，需要进行改进，一般改进的方法是对 $k$ 个近邻数据赋予权重，例如：距离测试样本越近，权重越大

KNN 工作机制十分简单：对于给定的测试样本，基于某种度量找出训练集中与该样本最靠近的 $k$ 个样本，然后基于这 $k$ 个邻居的信息进行预测，其算法流程如下：

对于给定的训练数据集 $T=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x_i} =(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}= \{c_1,c_2,…,c_K\}$ 为实例的类别

当给定一个实例特征向量 $\mathbf{x}$ 时，根据给定的距离度量，KNN 会在训练集 $T$ 中找出与 $\mathbf{x}$ 最近邻的 $k$ 个点，涵盖这 $k$ 个点的 $\mathbf{x}$ 的邻域记作 $N_k(\mathbf{x})$

在 $N_k(\mathbf{x})$ 中根据分类决策规则（如投票法）决定 $\mathbf{x}$ 的类别 $y$：

【距离度量】

在特征空间中，两个实例点的距离是这两个实例点的相似程度的反映

KNN 的特征空间一般是 $m$ 维实数向量空间 $\mathbb{R}^{m}$，常选用闵氏距离作为相似度度量标准

设特征空间 $\mathcal{X}$ 是 $m$ 维实数向量空间 $\mathbb{R}^m$，$\mathbf{x_i},\mathbf{x_j}\in \mathcal{X}$，且 $\mathbf{x_i}$ 和 $\mathbf{x_j}$ 满足 $\mathbf{x_i}=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})^T$，$\mathbf{x_j}=(x_j^{(1)},x_j^{(2)},…,x_j^{(m)})^T$

则 $\mathbb{x_i}$ 与 $\mathbb{x_j}$ 的闵氏距离定义为：

【近邻数 k】

近邻数 k，即在预测目标点时取 $k$ 个临近的点来预测，对于不同的样本，近邻数 $k$ 有着不同的取值，如何确定 $k$ 值获得最佳的结果是十分困难的

  • 当 $k$ 的取值过小时，一旦有噪声的成分存在，将会对预测产生比较大影响，容易发生过拟合
  • 当 $k$ 的取值过大时，就相当于用较大邻域中的训练实例进行预测，学习的近似误差会增大，这时与输入目标点较远实例也会对预测起作用，使预测发生错误

此外，对于 $k=1$ 的情况，称为最近邻算法，该算法将训练集中与输入实例 $x$ 最近邻点的类视为 $x$ 的类；而当 $k=n$，即取全部的实例时，无论输入的实例是什么，都将简单地预测其属于训练集中最多的类，此时模型过于简单，完全忽略了训练集中的信息，预测没有意义

同时，$k$ 的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，因为取偶数可能会产生相等的情况，不利于预测

在应用中，最常用的方法是从 $k=1$ 开始，使用检验集来估计分类器的误差率，然后不断重复该过程，每次令 $k$ 增加一个近邻，最后选取具有最小误差率的 $k$，一般来说，$k$ 的取值上限是 $\sqrt n$

【分类决策规则】

在 KNN 中，分类决策规则往往是多数表决（Majority Voting Rule），又称投票法，其是由输入实例的 $k$ 个邻近的训练样本中的多数类决定输入实例的类

对于给定的训练数据集 $T=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$，输入实例为 $\mathbf{x}$，则 $\mathbf{x}$ 的预测类别 $y$ 为：

若分类的损失函数为 0-1 损失函数，分类函数为：

设正确分类的概率为：

则误分类的概率为：

进一步，对于给定的输入实例 $\mathbf{x}\in\mathcal{X}$，其最近邻的 $k$ 个训练样本点构成集合 $N_k(x)$，若涵盖 $N_k(\mathbf{x})$ 的区域类别为 $c_j$，则正确分类率为：

故误分类率为：

要使误分类率即经验风险最小，就要使 $\sum\limits_{\mathbf{x_i}\in N_k(\mathbf{x})}I(y_i= c_j)$ 最大

因此，可以认为，多数表决规则等价于经验风险最小化

【实例】

假设在二维平面上，有四个点：$a_1(1,1)$、$a_2(1,2)$、$b_1(3,3)$、$b_2(3,4)$，其中，$a_1,a_2$ 属于 $A$ 类，$b1,b2$ 属于 $B$ 类

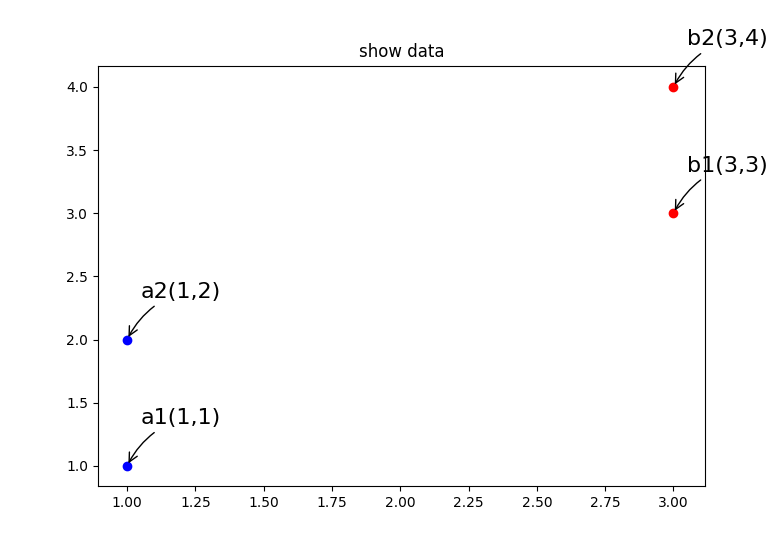
给出一个目标点 $c(2,1)$，现在想要知道对于 $c(2,1)$ 这个点来说，其属于 $A$ 类还是 $B$ 类

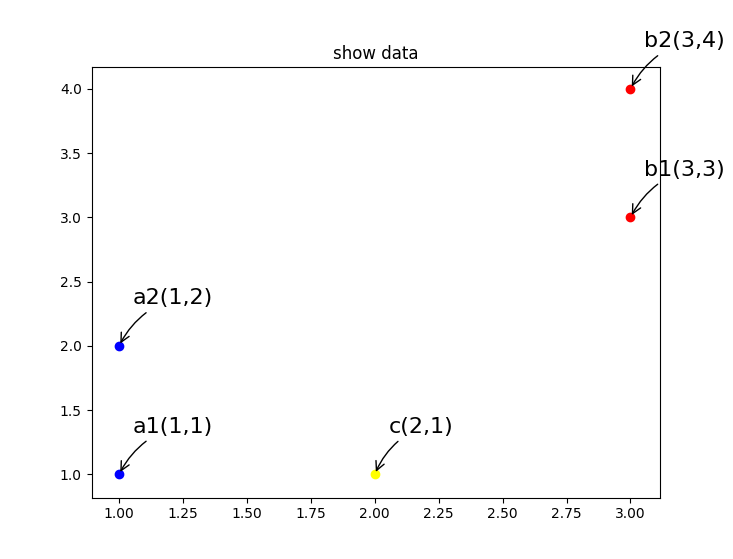
首先计算目标点 $c$ 到其他 $4$ 个点的距离，为方便计算，使用曼哈顿距离：

  • $M(a_1,c) = |1-2|+|1-1| = 1$
  • $M(a_2,c) = |1-2|+|2-1| = 2$
  • $M(b_1,c) = |3-2|+|3-1| = 3$
  • $M(b_2,c) = |3-2|+|4-1| = 4$

然后将计算出的距离集合按距离升序排序：

序号 点 类别 坐标 距离
$1$ $a_1$ $A$ $(1,1)$ $1$
$2$ $a_2$ $A$ $(1,2)$ $2$
$3$ $b_1$ $B$ $(3,3)$ $3$
$4$ $b_2$ $B$ $(3,4)$ $4$

接着取距离列表排序后的前 $k$ 个数据，这里令 $k=3$

序号 点 类别 坐标 距离
$1$ $a_1$ $A$ $(1,1)$ $1$
$2$ $a_2$ $A$ $(1,2)$ $2$
$3$ $b_1$ $B$ $(3,3)$ $3$

最后，统计这 $k$ 个数据里，出现频次最多的类别。

在该样例中，根据上表可以看出，$A$ 出现了两次，$B$ 出现了一次，因此我们认为点 $c$ 属于 $A$ 类

【sklearn 实现】

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现 K 近邻

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
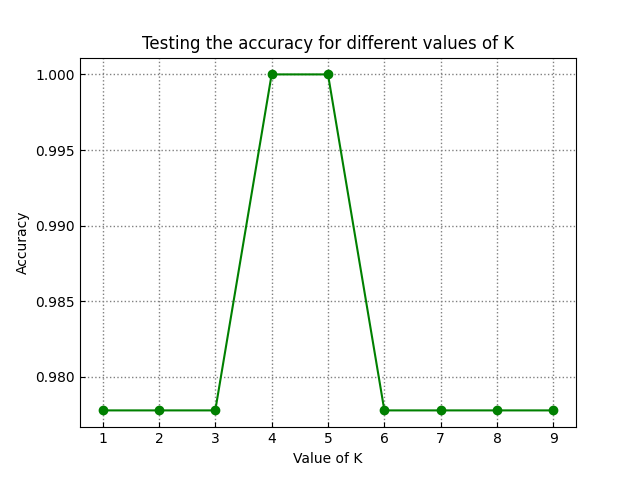
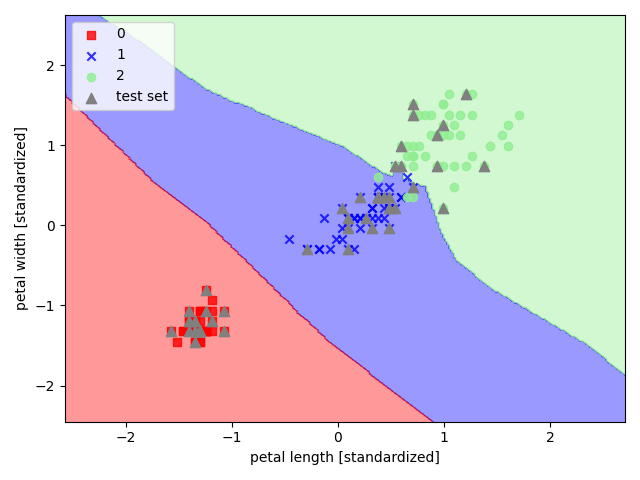
154
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target  #取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train, X_test):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 模型训练
def train_model(features, labels, k):
    # 建立 KNN 模型，采取 p=2 的闵氏距离，即标准欧式距离
    model = KNeighborsClassifier(n_neighbors=k, p=2, metric='minkowski')
    # 训练
    model.fit(features, labels)
    return model

# 尝试不同的k值以达到最好的准确率
def get_k(X_train, y_train, X_test, y_test):
    accuracy_list = []
    for k in range(1, 10):
        model = train_model(X_train, y_train, k)
        accuracy = model.score(X_test, y_test)
        accuracy_list.append(accuracy)
        
    # 绘制k-accuracy折线图
    plt.figure()
    plt.tick_params(direction='in')
    plt.grid(color='grey', linestyle=':', linewidth=1)
    plt.plot(range(1, 10), accuracy_list, color='green', marker='o')
    plt.xlabel('Value of K')
    plt.ylabel('Accuracy')
    plt.title('Testing the accuracy for different values of K')
    plt.show()
    
    # 寻找最大accuracy对应的k值
    k = accuracy_list.index(max(accuracy_list)) + 1 
    
    return k

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵，三分类情况下，大小为 3*3
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # macro 分类报告
    macro_class_report = classification_report(y_test, y_pred,target_names=["类0","类1","类2"])
    # 微精确率
    micro_p = precision_score(y_test,y_pred,average='micro') 
    # 微召回率
    micro_r = recall_score(y_test,y_pred,average='micro')
    # 微F1得分
    micro_f1 = f1_score(y_test,y_pred,average='micro') 
    
    indicators = {"cm2":cm2,"acc":acc,"acc_num":acc_num,"macro_class_report":macro_class_report,"micro_p":micro_p,"micro_r":micro_r,"micro_f1":micro_f1}
    return indicators

# 可视化
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 绘制决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 #第一个特征取值范围作为横轴
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 #第二个特征取值范围作为纵轴
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) # reolution为网格剖分粒度
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) # 对组合的特征进行预测，ravel为数组展平
    Z = Z.reshape(xx1.shape) # Z是列向量
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) # x和y为两个等长一维数组，z为二维数组，指定每一对xy所对应的z值
    plt.xlim(xx1.min(), xx1.max()) #对等高线间的区域进行填充
    plt.ylim(xx2.min(), xx2.max()) #对等高线间的区域进行填充
    
    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0, c='gray', marker='^', linewidths=1, s=55, label='test set')
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()
    
if __name__ == "__main__":
    # 特征提取
    X, y = deal_data()
    
    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
    
    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)
    
    # 获取最大accuracy下的k值
    k = get_k(X_train_std, y_train, X_test_std, y_test)
    print("k =", k)
    
    # 模型训练
    model = train_model(X_train_std, y_train, k)
    
    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test) # 测试集y值
    print("y pred:", y_pred) # 预测y值

    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"] 
    print("混淆矩阵：\n", cm2) 
    acc =  indicators["acc"]
    print("准确率：", acc)
    acc_num =  indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    macro_class_report = indicators["macro_class_report"]
    print("macro 分类报告：\n", macro_class_report)
    micro_p = indicators["micro_p"]
    print("微精确率：", micro_p)
    micro_r = indicators["micro_r"]
    print("微召回率：", micro_r)
    micro_f1 = indicators["micro_f1"]
    print("微F1得分：", micro_f1)

    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(105, 150))
感谢您对我的支持，让我继续努力分享有用的技术与知识点！