回归问题的评价指标（二）

Reference

• 回归评价指标MSE、RMSE、MAE、R-Squared
• R方的理解与用法
• Wikipedia entry on the Coefficient of determination
• 统计学——线性回归决定系数R2
• mse、rmse、mae、r2指标的总结以及局限性
• 可决系数

【概述】

在 回归问题的评价指标（一） 中，介绍了回归问题考虑经验风险 $R_{emp}(f)$ 时的评价指标 MSE、RMSE、MAE

但除这三个外，在回归问题中，进行拟合时，常采用相关系数（Correlation Coefficient）来研究变量间线性相关程度的量

在机器学习中，常采用可决系数（Coefficient of Determination）来估量回归方程拟合 $y$ 对 $x$ 的协变关系效果的量数

【皮尔逊相关系数 PCCs】

皮尔逊相关系数（Pearson Correlation Coefficient，PCCs）是衡量随机变量 X 与 Y 的相关程度的一种指标，其取值范围为 $[-1,1]$，相关系数的绝对值越大，则表明 $X$ 与 $Y$ 相关度越高

当 $X$ 与 $Y$ 线性正相关时，相关系数取值为 $1$；当 $X$ 与 $Y$ 线性负相关时，相关系数取值为 $-1$

对于两个随机变量 $X$、$Y$，他们的皮尔逊相关系数定义为 $X$ 与 $Y$ 间的协方差 $cov(X,Y)$ 和标准差 $\sigma_X,\sigma_Y$ 的商，即：

$$\begin{align*}\rho_{X,Y} &= \frac{cov(X,Y)}{\sigma_X\sigma _Y} \notag \\ &= \frac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X\sigma_Y} \notag \\ &= \frac{E(XY)-E(X)E(Y)}{\sqrt{E(X^2)-E^2(X)}\sqrt{E(Y^2)-E^2(Y)}} \notag \end{align*}$$

【可决系数 $R^2$】

总离差、可解释离差、不可解释离差

统计学中，一个特定数值对其平均值的偏离，被称为离差（Deviation）

在回归问题下，因变量 $y$ 的离差 $y-\overline{y}$ 被称为总离差（Total Dispersion），其可看作是由两部分合成的：一部分是因变量 $y$ 的回归拟合值 $\hat{y}$ 对均值 $\overline{y}$ 的离差 $ \hat{y}-\overline{y}$，另一部分是因变量 $y$ 对回归拟合值 $\hat{y}$ 的离差 $y-\hat{y}$

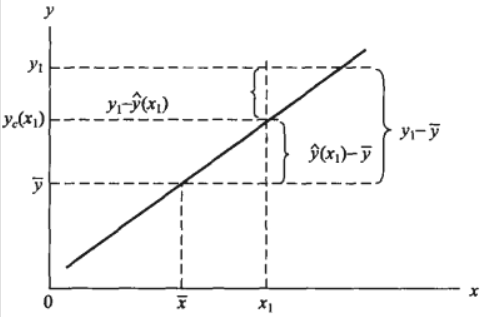
当 $x=\overline{x}$ 时，有 $\hat{y}-\overline{y} = 0$，可以发现，自变量 $x$ 的取值越偏离 $\overline{x}$，第一部分的离差就越大，即存在如下的函数关系：

$$\hat{y}-\overline{y}=a+b(x-\overline{x})$$

可以发现，第一部分的离差 $ \hat{y}-\overline{y}$ 完全是由因变量 $y$ 倚自变量 $x$ 的回归关系决定的，被称为可解释离差（Explained Deviation）

而第二部分的离差 $y-\hat{y}$ 是呈随机变化的，与回归关系无关，被称为不可解释离差（Unexplained Deviation）

那么，总离差、可解释离差、不可解释离差三者的关系如下：

$$y-\overline{y}=(\hat{y}-\overline{y}) - (y-\hat{y})$$

总平方和、回归平方和、残差平方和

一个变量的各数值对其平均值的偏离，被称为变异（Variation），通常用离差平方和（Sum of Squares of Deviations）来描述变异程度

对于样本数量为 $N$ 的测试集，总离差的平方和被称为总平方和（Sum of Squares for Total，SST），即：

$$SST=\sum_{i=1}^N (y_i-\overline{y})^2$$

可解释离差的平方和被称为回归平方和（Sum of Squares for Regression，SSR），又称解释平方和（ Explained Sum of Squares，ESS），即：

$$SSR=\sum_{i=1}^N(\hat{y_i}-\overline{y})^2$$

不可解释离差的平方和被称为残差平方和（Sum of Squares for Error，SSE）或（Residual Sum of Squares，RSS），即：

$$SSE=\sum_{i=1}^N(y_i-\hat{y_i})^2$$

易得：

$$SST=SSR+SSE$$

样本可决系数

对于 $SST=SSR+SSE$，将两边同时都除以 $SST$，可得：

$$\frac{\sum\limits_{i=1}^N(\hat{y_i}-\overline{y})^2}{\sum\limits_{i=1}^N(y_i-\overline{y})^2} + \frac{\sum\limits_{i=1}^N(y_i-\hat{y_i})^2}{\sum\limits_{i=1}^N(y_i-\overline{y})^2} = 1$$

这样就把在绝对数意义上对总离差的分割，改换成在相对数意义上对总离差的分割

其中，$\frac{\sum\limits_{i=1}^N(\hat{y_i}-\overline{y})^2}{\sum\limits_{i=1}^N(y_i-\overline{y_i})^2} $ 表示的是回归关系已经解释的 $y_i$ 值变异在其总变异中所占的比率，$\frac{\sum\limits_{i=1}^N(y_i-\hat{y_i})^2}{\sum\limits_{i=1}^N(y_i-\overline{y})^2}$ 表示的是回归关系不能解释的 $y_i$ 值变异在总变异中所占的比率

前者正是要寻求的用于估量回归方程拟合 $y$ 对 $x$ 的协变关系效果的量数，称为可决系数（Coefficient of Determination），其是由样本数据产生的，也被称为样本可决系数，用 $R^2$ 表示，即：

$$R^2 = 1 - \frac{\sum\limits_{i=1}^N(y_i-\hat{y_i})^2}{\sum\limits_{i=1}^N(y_i-\overline{y})^2}$$

$R^2$ 的含义是预测值 $\hat{y_i}$ 解释了真实值 $y_i$ 变量的方差的多大比例，衡量的是预测值 $\hat{y_i}$ 对于真实值 $y_i$ 的拟合程度

简单来说，假定 $y_i$ 的方差为 $1$ 个单位，那么 $R^2$ 表示使用该模型后，$y_i$ 的残差的方差减少了多少，假设 $R^2=0.8$，那么使用该模型后，残差的方差为真实值 $y_i$ 方差的 $20\%$

• $R^2=1$：是最理想的情况，此时所有预测值 $\hat{y_i}$ 等于真实值 $y_i$
• $R^2=0$：最可能的情况是所有预测值 $\hat{y_i}$ 等于平均值 $\overline{y}$
• $R^2<0$：模型的预测能力差，说明学习到的模型还不如基准模型，可能是数据中不存在线性关系

需要注意的是 $R^2$ 的最小值没有下限，因为预测可能出现任意程度的差，因此 $R^2$ 的取值范围是 $(-\infty,1]$

总体可决系数

总体可决系数是在总体中关于 $Y$ 总变异中总体回归方程 $\hat{Y}=\alpha + \beta{X}$ 已解释的变异所占比重的描述量数，其表示为：

$$\rho^2=1-\frac{\sigma^2_{y\cdot x}}{\sigma^2_{y}}$$

其中，$\sigma^2_{y\cdot x}$ 是围绕总体回归直线的方差，$\sigma^2_{y}$ 是围绕总体平均数的方差

$\rho^2$ 作为总体参数，通常视为未知的，需要用样本统计量去估计，将 $\sigma^2_{y\cdot x}$ 与 $\sigma^2_{y}$ 的无偏估计量分别代入上式，即可得 $\rho^2$ 的估计量的公式

$$\begin{align} R_c^2 &= 1 - \frac{S^2_{y\cdot x}}{S^2_{y}} \notag \\ &= 1 - \frac{\frac{1}{n-2}\sum\limits_{i=1}^N(y_i-\hat{y_i})^2 }{\frac{1}{n-1}\sum\limits_{i=1}^N(y_i-\overline{y})^2} \notag \end{align}$$

不难发现 $R^2$ 与 $R_c^2$ 的形式略有不同，前者采用的是平方和比率的形式，而后者采用的是均方和比率的形式

$R^2_c$ 被称为经调整样本拟合系数（Adjusted Coefficient of Determination），常用于对总体可决系数进行点估计，其平抑了方程中自变量数目的对解释作用的夸大

需要注意的是，在多元回归分析中，因为对同一样本 $m$ 个自变量的回归方程总比 $m-1$ 个自变量的回归方程求得已解释变差小，$R^2_c$ 在 $m$ 个自变量的方程中已解释离差除以 $(n-m-1)$，而在 $(m-1)$ 个自变量的方程中则除以 $(n-m-2)$