决策树的 CART 生成算法

Reference

• 回归树（Regression Tree）
• Regression Tree 回归树
• 决策树(分类树、回归树）
• 【机器学习】决策树（上）——ID3、C4.5、CART（非常详细）
• 决策树—ID3、C4.5、CART

【概述】

对于 ID3 和 C4.5 来说，它们只能用来解决分类为问题，因此都是分类决策树

而分类与回归树（Classification and Regression Tree，CART）既可以用于分类也可以用于回归，只是在生成决策树的过程中，所选取的特征选择的标准不同

其假设决策树是二叉树，分支结点的取值为 是 和 否，左分支取值为 是，右分支取值为 否

其等价于递归地二分每个特征，将输入空间分为有限个单元，并在这些单元上确定预测的概率分布，即输入给定的条件下输出的条件概率分布

与 C4.5 一样，CART 算法由以下两步组成：

1. 决策树生成：使用基尼系数或均方误差作为特征选择的标准，基于训练集生成决策树
2. 决策树剪枝：采用代价复杂度剪枝策略，利用验证集对已生成的树进行剪枝

【CART 分类树】

使用 CART 来构建分类树的流程，与 ID3 和 C4.5 相似，只是采用了基尼指数作为特征选择的标准

下面直接给出 CART 生成分类树的算法：

输入：训练集 $D$

输出：决策树

根据训练集，从根结点开始，递归地对每个结点进行以下操作，构建一棵二叉决策树：

Step1：设当前结点的训练集为 $D$，计算现有特征对该数据集的基尼指数

此时，对每一个特征 $A$，对其可能取的每个值 $a$，根据样本点对 $A=a$ 的测试为 是、否，将 $D$ 分割成 $D_1$ 和 $D_2$ 两个部分，利用下式计算 $A=a$ 时的基尼指数

$$Gini(G,A)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$$

Step2：在所有可能的特征 $A$ 以及它们所有可能的切分点 $a$ 中，选择基尼指数最小的特征及其对应的切分点，作为最优特征和最优切分点

根据最优特征与最优切分点，从现结点生成两个子结点，将训练集依照特征分配到两个子结点中

Step3：对两个子结点递归地调用 Step1 与 Step2，直到满足停止条件

Step4：生成 CART 决策树

【CART 回归树】

假设形式

回归树，就是用树模型处理回归问题，此时采用均方误差作为特征选择的标准

对于给定容量为 $n$ 的训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x_i}=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出为 $y_i$，其是一个连续变量

回归问题的目标是构造一个函数 $f(\mathbf{x})$ 能够拟合数据集 $D$ 中的元素，使得均方误差 MSE 最小，即：

$$\min \quad \frac{1}{n}\sum_{i=1}^n (f(\mathbf{x}_i)-y_i)^2$$

一棵回归树对应着整个特征空间上递归地二分类的划分，在每一个划分单元上都有一个输出值，下面用数学语言来进行描述：

假设对于给定训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，用该训练集构建好的一棵 CART 回归树有 $K$ 个叶结点，这意味着将输入空间划分为 $K$ 个单元 $R_1,R_2,…,R_K$，且 CART 最多会有 $K$ 个不同的预测值，即每一个叶结点都对应一个单元 $R_k$，同时该单元输出一个预测值

用 $c_k$ 表示第 $k$ 个叶结点的预测值，其一般是该叶结点所含训练集样本输出的均值，即：

$$c_k = \text{average} (y_i|\mathbf{x}_i\in R_k)$$

则回归树的模型表示为：

$$f(\mathbf{x}_i)=\sum_{j=1}^Kc_k\mathbb{I}(\mathbf{x}_i\in R_k)$$

此时，CART 最小化 MSE 公式如下：

$$\min \quad \frac{1}{n}\sum_{k=1}^K\sum_{\mathbf{x}_i\in R_k}(c_k-y_i)^2$$

划分过程

根据 CART 是二叉树的特征，在每一次划分中，都需要进行一次特征选择，同时将该特征空间一分为二的切分，使得模型在训练集上 MSE 最小，即每个叶结点的 MSE 之和最小

也就是说，要确定两方面的内容：

1. 选择哪一个特征来进行划分
2. 对于指定的划分特征，选择什么样的切分点

针对上述的两个问题，采用启发式方法，选择输入 $\mathbf{x}_i$ 的第 $j$ 个特征 $x_i^{(j)}$与其取值 $s$，作为切分变量（Splitting Variable）和切分点（Splitting Point）

此时，切分变量和切分点将父结点的输入空间一分为二，即：

$$\left\{\begin{array}{rl} R_1(j,s)=\{\mathbf{x}_i|x_i^{(j)}\leq s\} \\ R_2(j,s)=\{\mathbf{x}_i|x_i^{(j)}>s\} \end{array}\right.$$

进一步，寻找最优切分变量 $j$ 和最优切分点 $s$，即求解如下公式：

$$\min_{j,s} \bigl[ \min_{c_1}\sum\limits_{\mathbf{x}_i\in R_1(j,s)}(c_1-y_i)^2+\min_{c_2}\sum\limits_{\mathbf{x}_i\in R_2(j,s)}(c_2-y_i)^2 \bigr]$$

该公式说明了，在要求切分点 $s$ 两边区域的均方差尽量小的同时，保证两区域的最小均方差的和是最小的

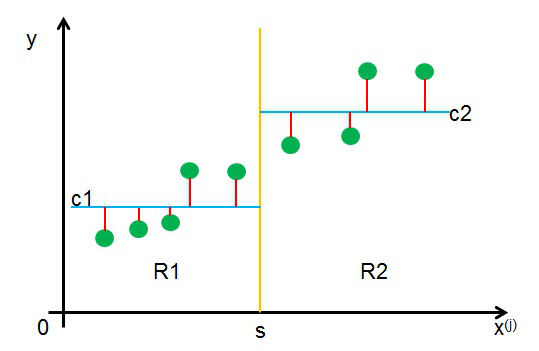
对于每一个特征 $j$ 进行遍历，每一个 $j$ 的取值都能通过上式得到一个最优切分点 $s$，以及此时求出的上式的值 $A_{j,s}$，最终比较所有的 $A_{j,s}$，选择其中最小的那个对应的 $(j,s)$ 作为最优切分变量和切分点，将特征空间划分为两个部分

此时，对于最小化公式中的 $c_1$ 和 $c_2$，取最优值：

$$\left\{\begin{array}{rl} \hat{c_1}=\text{ave}(y_i|\mathbf{x}_i\in R_1) \\ \hat{c_2}=\text{ave}(y_i|\mathbf{x}_i\in R_2) \end{array}\right.$$

之后，对两个子空间 $R_1$、$R_2$ 重复上述划分过程，直到满足停止条件为止，生成一棵决策树

最小二乘回归树生成算法

按照上述过程生成的决策树，称为最小二乘回归树（Least Squares Regression tree），下面给出最小二乘回归树生成算法：

输入：训练集 $D$

输出：决策树 $f(\mathbf{x})$

在训练集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域的输出值，构建二叉决策树：

1.选择最优切分变量 $j$ 和切分点 $s$，求解：

$$\min_{j,s} \bigl[ \min_{c_1}\sum\limits_{\mathbf{x}_i\in R_1(j,s)}(y_i-c_1)^2+\min_{c_2}\sum\limits_{\mathbf{x}_i\in R_2(j,s)}(y_i-c_2)^2 \bigr]$$

遍历特征 $j$，对固定的切分变量 $j$ 扫描切分点 $s$，选择使上式达到最小值的 $(j,s)$ 对

2.用选定的 $(j,s)$ 对，划分区域

$$\left\{\begin{array}{rl} R_1(j,s)=\{\mathbf{x}_i|x_i^{(j)}\leq s\} \\ R_2(j,s)=\{\mathbf{x}_i|x_i^{(j)}>s\} \end{array}\right.$$

3.根据划分的 $R_1$、$R_2$ 区域，确定相应的输出值

$$\left\{\begin{array}{rl} \hat{c_1}=\text{ave}(y_i|\mathbf{x}_i\in R_1) \\ \hat{c_2}=\text{ave}(y_i|\mathbf{x}_i\in R_2) \end{array}\right.$$

4.递归的对两个子区域执行步骤 1、2、3，直到满足停止条件

5.将输入空间划分为 $K$ 个区域 $R_1,R_2,…,R_K$，生成决策树

$$f(\mathbf{x}_i)=\sum_{k=1}^K\hat{c_k}\mathbb{I}(\mathbf{x}_i\in R_k)$$

【CART 剪枝】

CART 算法使用的剪枝策略是代价复杂度剪枝策略，其由两步组成：

1. 从生成算法产生的决策树 $T_0$ 底端开始不断剪枝，直到 $T_0$ 的根结点，形成一个子树序列 $\{T_0,T_1,…,T_n\}$
2. 在独立的验证数据集上，对子树序列进行测试，从中选择最优子树

关于代价复杂度剪枝的具体介绍，详见：决策树的剪枝策略

【ID3 和 C4.5 无法处理回归问题的原因】

CART 是一棵二叉树，那么只要回归树不是一棵二叉树，那么就不是 CART 树

在分类问题中，ID3、C4.5 和 CART 的区别就在于特征选择的策略不同，信息增益、信息增益比、基尼指数

在回归问题中，用均方误差最小的准则求解每个特征上的最优输出值，这种情况下，分类时的 ID3、C4.5、CART 之间的区别就没了，那么问题就变成每个父结点划分成多少个子结点的问题了

因此，如果还是二叉树，那么就认为是 CART 回归树，否则就不是