Alex_McAvoy

想要成为渔夫的猎手

软间隔支持向量机

发表于 分类于 ， ，
本文字数： 11k 阅读时长 ≈ 10 分钟

References：

【引入】

硬间隔支持向量机是用来解决训练集完全线性可分情况的二分类模型，但在实际应用中，由于实际获取的真实样本往往会存在噪声，使得训练数据不是清晰线性可分的，又或者即使找到了一个可以使不同类样本完全分开的超平面，也很难确定这个线性可分的结果是不是由于过拟合导致的

也就是说，训练集中存在一些特异点（Outlier），将这些特异点去除后，剩余大部分的样本点的集合是线性可分的，这被称为近似线性可分

对于近似线性可分的训练集，引入了软间隔（Soft Margin）这个概念，并将求解硬间隔最大化问题改为求解软间隔最大化问题，从而使得硬间隔支持向量机更一般化，能够对近似线性可分的数据进行处理

【假设形式】

对于给定容量为 $n$ 的线性不可分训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(n)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}=\{+1,-1\}$

软间隔支持向量机（Soft Margin Support Vector Machines）对于线性不可分的训练集，通过求解软间隔最大化问题：

其中，$\xi_i\geq 0$ 是为每个样本点 $(\mathbf{x}_i,y_i)$ 引入的松弛变量，$C>0$ 是惩罚系数

得到最优分离超平面：

以及相应的分类决策函数：

由于现实中的训练数据往往存在噪声或特异点，是线性不可分的，因此软间隔支持向量机具有更广的适用性

同时，由于软间隔支持向量机是在硬间隔支持向量机基础上针对训练数据线性不可分时的改进，因此又称线性支持向量机（Linear Support Vector Machines）

也就是说，线性（软间隔）支持向量机包含线性可分（硬间隔）支持向量机

【软间隔支持向量机学习算法的原始形式】

软间隔最大化

软间隔最大化（Soft Margin Maximization）同样是找到使所有样本点的几何间隔的最小值最大的分离超平面，即寻找最大间隔分离超平面

对于硬间隔最大化中的原始问题：

线性近似可分意味着某些样本点 $(\mathbf{x}_i,y_i)$ 不能满足函数间隔大于等于 $1$ 的约束条件 $y_i(\boldsymbol{\omega}\cdot\mathbf{x}+\theta)-1\geq 0$

为解决这个问题，可以对每个样本点 $(\mathbf{x}_i,y_i)$ 引入一个松弛变量 $\xi_i\geq 0$，使得函数间隔加上松弛变量大于等于 $1$，即：

同时，对每个松弛变量 $\xi_i$，支付一个代价 $\xi_i$，使得目标函数由 $\frac{1}{2}||\boldsymbol{\omega}||_2^2$ 变为：

其中，$C>0$ 为惩罚系数，由具体的应用问题决定，$C$ 越大说明对误分类的惩罚越大

此时的目标函数有两层含义，一是使 $\frac{1}{2}||\boldsymbol{\omega}||_2^2$ 尽量小，即令几何间隔尽量大，二是令误分类点的个数尽量小，并通过惩罚系数 $C$ 来调和二者的关系

于是可以得到约束最优化问题：

上述的约束最优化问题是一个凸二次规划（Convex Quadratic Programming）问题，相对于硬间隔最大化，其被称为软间隔最大化

需要注意的是，对于上述的凸二次规划问题，关于 $(\boldsymbol{\omega},\theta,\boldsymbol{\xi})$ 的解是存在的，同时 $\boldsymbol{\omega}$ 的解是唯一的，但 $\theta$ 的解可能不唯一，其存在于一个区间中

最大间隔法

软间隔支持向量机的学习算法为最大间隔法

输入：容量为 $n$ 的训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}=\{+1,-1\}$

输出：最大间隔分离超平面、分类决策函数

算法步骤：

Step1：构造并求解如下约束最优化问题

求得最优解 $\boldsymbol{\omega}^*$ 和 $\theta^*$

Step2：根据最优解 $\boldsymbol{\omega}^*$ 和 $\theta^*$，得到分离超平面

以及分类决策函数

【软间隔支持向量机学习算法的对偶形式】

对偶问题的转化

为求解软间隔支持向量机的最优化问题：

将其作为原始最优化问题，应用拉格朗日对偶性，通过求解对偶问题来得到原始问题的最优解

首先，构建拉格朗日函数，即为每一个不等式约束引入拉格朗日乘子 $\lambda_i\geq 0$ 和 $\mu_i\geq 0$，即：

其中，$\boldsymbol{\lambda}=(\lambda_1,\lambda_2,\cdots,\lambda_n)^T$ 和 为拉格朗日乘子向量

此时，根据拉格朗日对偶性，原始问题的对偶问题就变为了极大极小问题，即：

因此，为了得到对偶问题的解，就要先求拉格朗日函数 $L(\boldsymbol{\omega},\theta,\boldsymbol{\xi},\boldsymbol{\lambda},\boldsymbol{\mu})$ 对 $\boldsymbol{\omega}$、$\theta$、$\boldsymbol{\xi}$ 的极小，再求对 $\boldsymbol{\lambda}$、$\boldsymbol{\xi}$ 的极大

对偶问题中的极小问题

对于对偶问题中的极小问题：

令拉格朗日函数 $L(\boldsymbol{\omega},\theta,\boldsymbol{\xi},\boldsymbol{\lambda},\boldsymbol{\mu})$ 分别对 $\boldsymbol{\omega}$、$\theta$、$\boldsymbol{\xi}$ 求偏导，并令其等于 $0$，即：

可得：

将上式带回拉格朗日函数 $L(\boldsymbol{\omega},\theta,\boldsymbol{\xi},\boldsymbol{\lambda},\boldsymbol{\mu})$ 中，有：

故有：

对偶问题中的极大问题

对于对偶问题中的极大问题：

即为对偶问题，有：

利用等式约束 $C-\lambda_i-\mu_i=0$，消去 $\mu_i$，有：

再将该问题的目标函数由求极大转为求极小，就得到如下的等价的对偶最优化问题：

可以发现，原始问题是凸优化问题，且 Slater 条件成立，那么，原始问题强对偶性成立，即求解原始问题可以转换为求解上述的对偶问题

假设上述的对偶问题对 $\boldsymbol{\lambda}$ 的一个解为 $\boldsymbol{\lambda}^* = (\lambda_1^*,\lambda_2^*,\cdots,\lambda_n^*)^T$，那么根据 KKT 条件，可得：

故而有：

同时，若存在 $0<\lambda_j^*<C$，对此 $j$ 有：

将 $\boldsymbol{\omega}^* = \sum\limits_{i=1}^n \lambda_i^* y_i\mathbf{x}_i$ 带入到上式，并由 $y_j^2=1$，可得：

故而，分离超平面可写为：

分类决策函数可写为：

对偶学习算法

根据上述对偶问题的推导，可得到软间隔支持向量机的对偶学习算法

输入：容量为 $n$ 的近似线性可分的训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}=\{+1,-1\}$

输出：最大间隔分离超平面、分类决策函数

算法步骤：

Step1：选择惩罚系数 $C>0$，构造并求解如下约束最优化问题（原始问题的对偶问题）

求得最优解 $\boldsymbol{\lambda}^* = (\lambda_1^*,\lambda_2^*,\cdots,\lambda_n^*)^T$

Step2：根据最优解 $\boldsymbol{\lambda}^*$，计算分离超平面的法向量 $\boldsymbol{\omega}^*$ 和截距 $\theta^*$

对于法向量 $\boldsymbol{\omega}^*$，有：

选择最优解 $\boldsymbol{\lambda}^*$的一个分量 $\lambda_j^*$，满足 $0<\lambda_j^*<C$，计算截距 $\theta^*$，有：

Step3：根据最优解 $\boldsymbol{\omega}^*$ 和 $\theta^*$，得到分离超平面

以及分类决策函数

对于 Step1 中的凸二次规划问题，可使用 SMO 算法来求解，关于 SMO 算法，详见：序列最小最优化算法 SMO

在 Step2 中，对任一满足 $0<\lambda_j^*<C$ 的 $\lambda_j^*$，均可求出截距 $\theta^*$，从理论上来说，原始问题对 $\theta$ 的解可能不唯一，然而在实际应用中，往往只会出现上述算法叙述的情况

【支持向量与间隔边界】

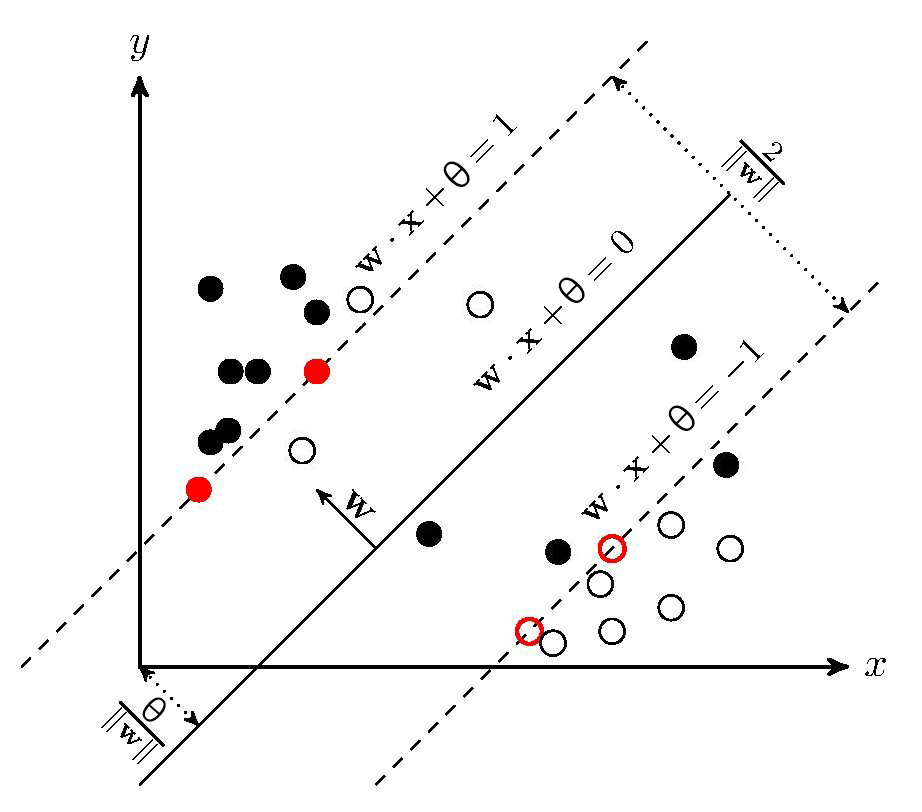
在线性不可分的情况下，对于对偶问题的解 $\boldsymbol{\lambda}^* = (\lambda_1^*,\lambda_2^*,\cdots,\lambda_n^*)^T$ 中对应 $\lambda_i^*>0$ 的样本点 $(\mathbf{x}_i,y_i)$ 的实例 $\mathbf{x_i}$ 称为软间隔的支持向量（Support Vector）

如图所示，红线标出的是支持向量 $\mathbf{x}_i$ 到间隔边界的距离 $\frac{1}{||\boldsymbol{\omega}_2^2||}\xi_i$

此外，分类决策函数：

根据 KKT 条件，对于任意样本 $(\mathbf{x}_i,y_i)$，总有 $\lambda_i=0$ 或 $y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)=1-\xi_i$

  • 当 $\lambda_i=0$ 时，该样本不会在分类决策函数 $f(\mathbf{x})$ 求和中出现，也就不会对 $f(\mathbf{x})$ 造成任何影响
  • 当 $\lambda_i>0$ 时，必有 $y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)=1-\xi_i$，所对应的样本点正好位于间隔边界上，是一个支持向量
    • 若 ，则 $\mu_i>0$，进而有 $\xi_i=0$，相应的支持向量 $\mathbf{x}_i$ 恰好落在间隔边界上
    • 若 $\lambda_i=C$，则 $\mu_i=0$，此时若 $\xi_i=0$，即分类正确，$\mathbf{x}_i$ 位于间隔边界与分离超平面之间
    • 若 $\lambda_i=C$，则 $\mu_i=0$，此时若 $\xi_i=1$，$\mathbf{x}_i$ 位于分离超平面上
    • 若 $\lambda_i=C$，则 $\mu_i=0$，此时若 $\xi_i>1$，即分类错误，$\mathbf{x}_i$ 位于分离超平面误分一侧

【软间隔支持向量机的等价问题】

最优化问题

对于软间隔支持向量机来说，其模型为分离超平面 $S:\boldsymbol{\omega}^*\cdot \mathbf{x}+\theta^*=0$ 以及分类决策函数 $f(\mathbf{x}) = \text{sign}(\boldsymbol{\omega}^*+\theta^*)$，学习策略为软间隔最大化，学习方法为凸二次规划

对于原始问题：

其等价于最优化：

证明：

对于最优化问题：

取 $\xi_i=\max(0,1-y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta))$，当 $1-y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)>0$ 时，有 $\xi_i>0$，进而有：

当 $1-y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)\leq0$ 时，有 $\xi_i=0$，进而有：

此时，满足原始问题的不等式约束，故最优化问题可写为：

进一步，取 $\lambda=\frac{1}{2C}$，则有：

与原始问题等价

反之，也可将原始问题表示为上述的最优化问题

合页损失函数

对于最优化问题

其中，目标函数第一项中的 $\max(0,1-y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta))$ 被称为合页损失函数（Hinge Loss Function），当样本点 $(\mathbf{x}_i,y_i)$ 被正确分类且函数间隔 $y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)>1$ 时，损失是 $0$，否则损失是 $1-y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)$，第二项 $\lambda||\boldsymbol{\omega}||_2^2$ 是正则化项

如下图所示，横轴是函数间隔 $y(\boldsymbol{\omega}\cdot \mathbf{x}+\theta)$，纵轴是损失，函数的形状如同一个合页，因此被称为合页损失函数，图中还画出了 0-1 损失函数，可以认为其是二分类问题真正的损失函数，合页损失函数是 0-1 损失函数的上界

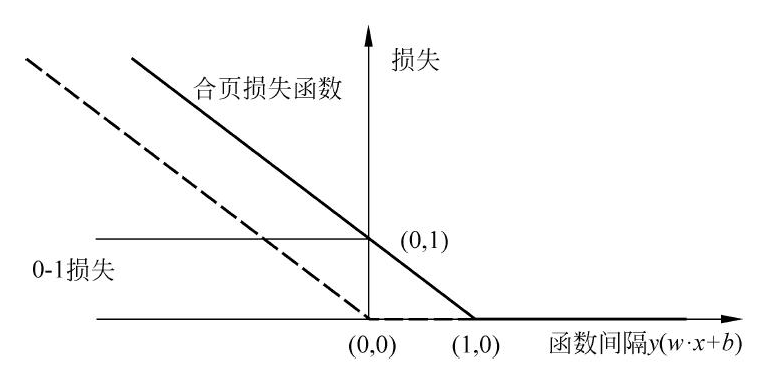
由于 0-1 损失函数不是连续可导的，直接优化由其构成的目标函数较为困难，可以认为软间隔支持向量机是由优化 0-1 损失函数的上界（合页损失函数）构成的目标函数

此外，图中的虚线代表的是感知机中所使用的感知损失函数（Perceptron Loss Function）

当样本点 $(\mathbf{x}_i,y_i)$ 被正确分类时，损失是 $0$，否则损失是 $-y_i(\boldsymbol{\omega}\cdot \mathbf{x}_i+\theta)$，相比之下，合页损失函数不仅要求分类正确，而其确信度足够高时是损失才是 $0$，即合页损失函数对学习有更高的要求

【sklearn 实现】

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现软间隔支持向量机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target  #取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train,X_test):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 模型训练
def train_model(X_train_std, y_train):
    # 建立软间隔SVM模型
    model = LinearSVC(penalty='l2',loss='hinge',C=5,random_state=1)
    # 训练
    model.fit(X_train_std, y_train)
    return model

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵，三分类情况下，大小为 3*3
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # macro 分类报告
    macro_class_report = classification_report(y_test, y_pred,target_names=["类0","类1","类2"])
    # 微精确率
    micro_p = precision_score(y_test,y_pred,average='micro') 
    # 微召回率
    micro_r = recall_score(y_test,y_pred,average='micro')
    # 微F1得分
    micro_f1 = f1_score(y_test,y_pred,average='micro') 
    
    indicators = {"cm2":cm2,"acc":acc,"acc_num":acc_num,"macro_class_report":macro_class_report,"micro_p":micro_p,"micro_r":micro_r,"micro_f1":micro_f1}
    return indicators

# 可视化
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 绘制决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 #第一个特征取值范围作为横轴
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 #第二个特征取值范围作为纵轴
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) # reolution为网格剖分粒度
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) # 对组合的特征进行预测，ravel为数组展平
    Z = Z.reshape(xx1.shape) # Z是列向量
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) # x和y为两个等长一维数组，z为二维数组，指定每一对xy所对应的z值
    plt.xlim(xx1.min(), xx1.max()) #对等高线间的区域进行填充
    plt.ylim(xx2.min(), xx2.max()) #对等高线间的区域进行填充
    
    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0, c='gray', marker='^', linewidths=1, s=55, label='test set')
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()
    
if __name__ == "__main__":
    # 特征提取
    X, y = deal_data()
    
    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
    
    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)
    
    # 模型训练
    model = train_model(X_train_std, y_train)
    
    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test) # 测试集y值
    print("y pred:", y_pred) # 预测y值
    
    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"] 
    print("混淆矩阵：\n", cm2) 
    acc =  indicators["acc"]
    print("准确率：", acc)
    acc_num =  indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    macro_class_report = indicators["macro_class_report"]
    print("macro 分类报告：\n", macro_class_report)
    micro_p = indicators["micro_p"]
    print("微精确率：", micro_p)
    micro_r = indicators["micro_r"]
    print("微召回率：", micro_r)
    micro_f1 = indicators["micro_f1"]
    print("微F1得分：", micro_f1)
    
    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(105, 150))
感谢您对我的支持，让我继续努力分享有用的技术与知识点！