Kruskal 算法

【基本思想】

$Kruskal$ 算法基本思想是并查集思想

初始时，将所有边升序排序，认为每一个点都是孤立的，分属 $n$ 个独立的集合

之后，按顺序枚举每一条边：

1. 若这条边连接的两个点分属两个不同的集合，那么就将这条边加入最小生成树，即这两个不同的集合合并为一个集合
2. 若这条边连接的两个点属于同一集合，那么就跳过

重复上述过程，直到选取 $n-1$ 条边为止（只剩一个集合）

其时间复杂度为：$O(|E|log|E|)$，仅与图的边数有关，适合顶点多的稀疏图

【算法分析】

以下图为例

开始时，存在 $5$ 个集合 {1},{2},{3},{4},{5}，生成树中没有边，MST=0

第一次选择 $(1,2)$ 这条边，将边加入生成树中，将两个顶点 $1$，$2$ 合并为一个集合

此时，有 $4$ 个集合 {1,2},{3},{4},{5}，$1$ 条边 {(1,2)}，MST=2

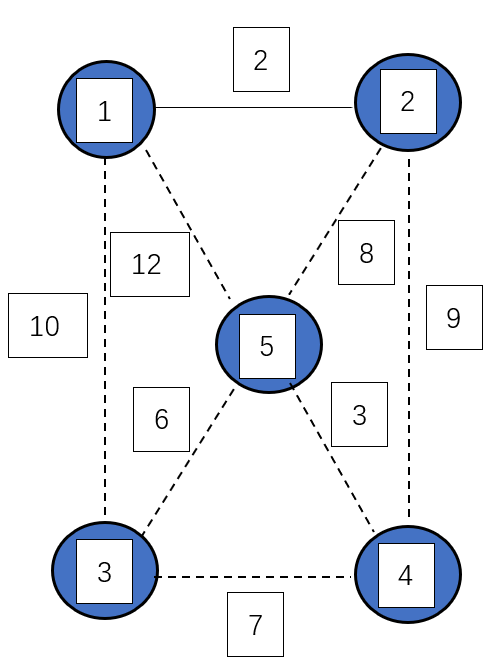
第二次选择的是 $(4,5)$ 这条边，将这条边加入生成树中，将两个顶点 $4$，$5$ 合并为一个集合

此时，有 $3$ 个集合 {1,2},{3},{4,5}，$2$ 条边 {(1,2),(4,5)}，MST=5

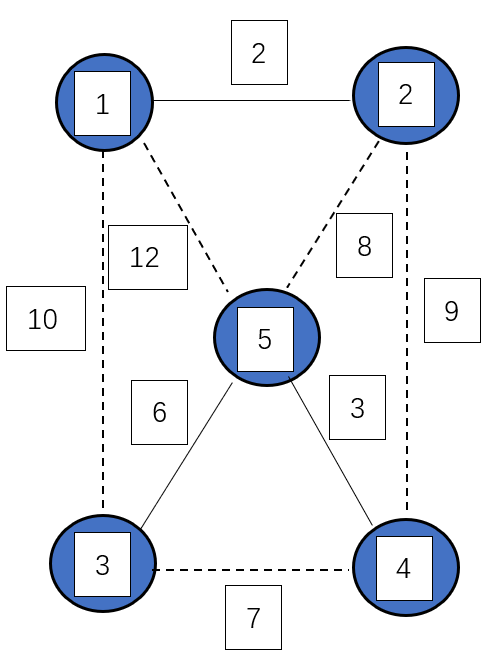
第三次选择的是 $(3,5)$ 这条边，将这条边加入生成树中，将它的两个顶点 $3$，$5$ 所在的两个集合合并为一个集合

此时，有 $2$ 个集合 {1,2},{3,4,5}，$3$ 条边 {(1,2),(4,5),{3,5}}，MST=11

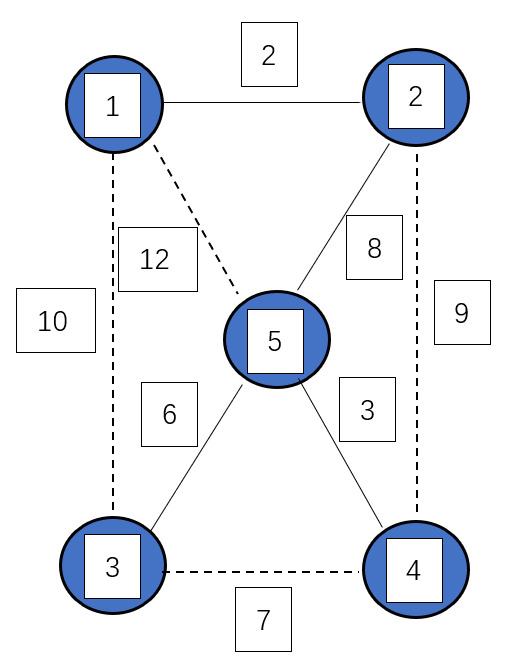
第三次选择的是 $(2,5)$ 这条边，将这条边加入生成树中，将它的两个顶点 $2$，$5$ 所在的两个集合合并为一个集合

此时，有 $1$ 个集合 {1,2,3,4,5}，$4$ 条边 {(1,2),(4,5),{3,5},{2,5}}，MST=19

【实现】

struct Edge {
    int x, y;
    int dis;
    bool operator<(Edge K) const { return dis < K.dis; }
} edge[N];
int father[N];    //并查集父结点
int Find(int x) { //并查集查询根结点
    if (father[x] == x)
        return x;
    return father[x] = Find(father[x]);
}
int kruskal(int n, int m) {
    for (int i = 1; i <= n; i++) //并查集初始化
        father[i] = i;
    
    sort(edge + 1, edge + m + 1); //边升序排序

    int MST = 0;
    int edgeNum = 0; //边数
    for (int i = 1; i <= m; i++) {
        int fx = Find(edge[i].x); //点x的根结点
        int fy = Find(edge[i].y); //点y的根结点
        if (fx != fy) { //合并
            father[fx] = fy;
            MST += edge[i].dis;
            edgeNum++;
        }
        if (edgeNum == n - 1) { // n-1条边时停止
            return MST;
        }
    }
}
int main() {
    int n, m;
    scanf("%d%d", &n, &m); //n个结点m条边
    for (int i = 1; i <= m; ++i)
        scanf("%d%d%d", &edge[i].x, &edge[i].y, &edge[i].dis);
    int MST = kruskal(n, m);
    printf("%d\n", MST);
    return 0;
}