Prim 算法

【基本思想】

Prim 算法基本思想是贪心的蓝白点思想，用白点代表已进入最小生成树的点，蓝点代表未进入最小生成树的点，初始时，所有的点都是蓝点

每次循环都将一个蓝点 $u$ 变为白点，并且此蓝点 $u$ 与白点相连的最小边权 $min[u]$ 是当前所有蓝点中最小的

这相当于每次循环让一个新的点加入生成树，让一条最小边加入生成树，$n-1$ 次循环就能生成一棵含有 $n$ 个点的树，最后得到的一定是最小生成树

其时间复杂度为：$O(|V|^2)$，仅与点数有关，适合稠密图

【算法分析】

以下图为例，蓝点和虚线代表未进入最小生成树的点、边，白点和实现代表已进入最小生成树是点、边

初始时，所有点都是蓝点，dis[1] = 0，dis[2] ~ dis[5] = INF，权值和 MST = 0

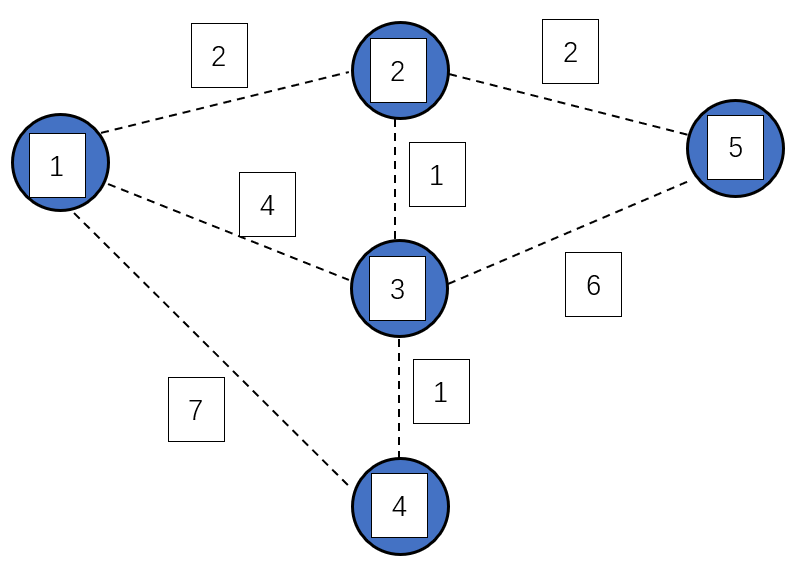
第一次循环找到 dis[1] = 0 最小的蓝点 $1$，将 $1$ 变为白点，接着枚举与 $1$ 相连的所有蓝点 $2$，$3$，$4$，修改它们与白点相连的最小边权

故有：dis[2] = G[1][2] = 2，dis[3] = G[1][3] = 4，dis[4] = G[1][4] = 7，MST = 0

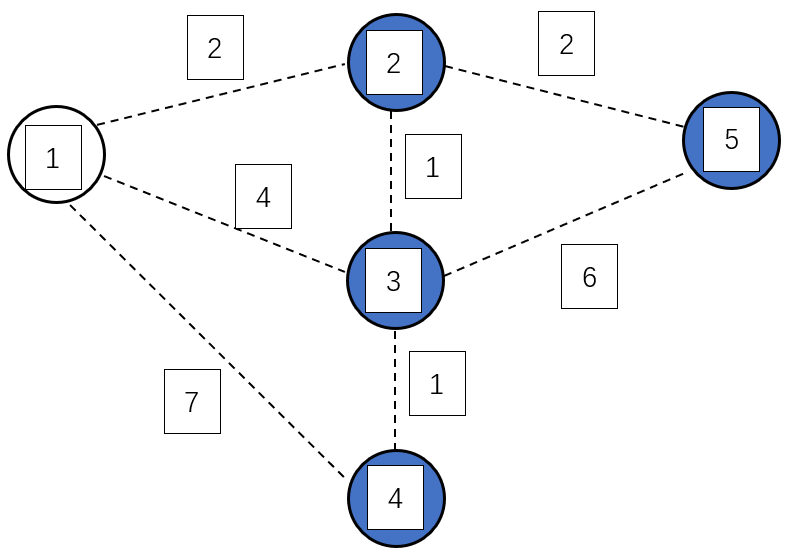
第二次循环是找到 dis[2] 最小的蓝点 $2$，将 $2$ 变为白点，接着枚举与 $2$ 相连的所有蓝点 $3$，$5$，修改它们与白点相连的最小边权

故有：dis[3] = G[2][3] = 1，dis[5] = G[2][5] = 2，MST = 2

第三次循环是找到 dis[3] 最小的蓝点 $3$，将 $3$ 变为白点，接着枚举与 $3$ 相邻的所有蓝点 $4$，$5$，修改它们与白点相连的最小边权

故有：dis[4] = G[3][4] = 1

同时，由于 dis[5] = 2 < G[3][5] = 6，所以不修改 dis[5] 的值，即 MST = 3

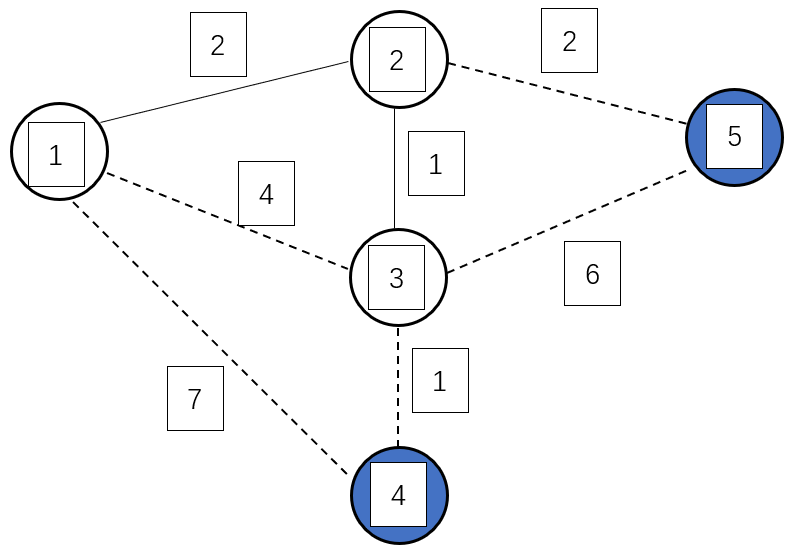
最后两轮循环将点 $4$，$5$ 以及边 G[2][5]，G[3][4] 添加进最小生成树

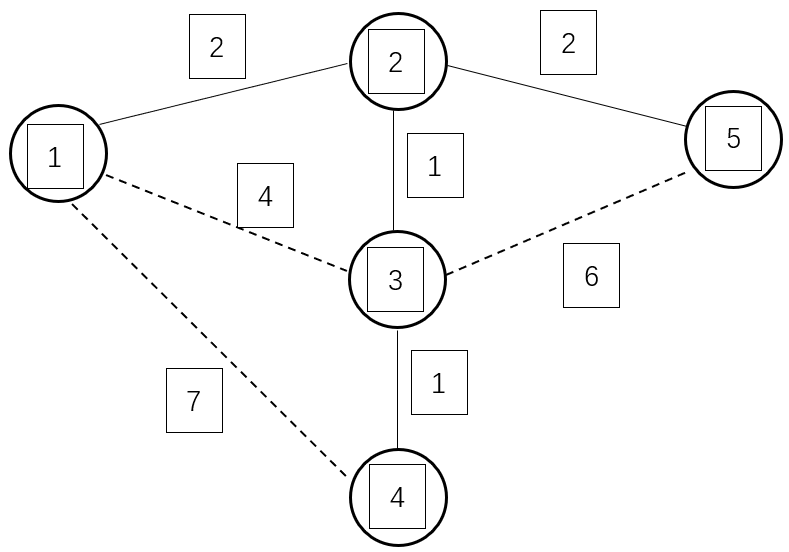
最后权值之和 MST = 6

【实现】

#define INF 0x3f3f3f
int G[N][N]; //邻接矩阵
int dis[N];  //权值数组
bool vis[N]; //蓝白点标记数组
int Prim(int n, int m) {
    for (int i = 1; i <= n; i++) {
        int k;
        int minn = INF;
        for (int j = 1; j <= n; j++) { //枚举所有点
            if (!vis[j] && dis[j] < minn) { //寻找与白点相连的权值最小的蓝点u
                minn = dis[j];
                k = j;
            }
        }
        vis[k] = true;               //蓝点u加入生成树，标记为白点
        for (int j = 1; j <= n; j++) //修改所有与u相连的蓝点
            if (!vis[j] && dis[j] > G[k][j])
                dis[j] = G[k][j];
    }

    int MST = 0;
    for (int i = 1; i <= n; i++) //权值和的计算
        MST += dis[i];
    return MST;
}
int main() {
    int n, m; //n个点m条边
    scanf("%d%d", &n, &m);
    memset(vis, false, sizeof(vis));
    memset(dis, INF, sizeof(dis));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            scanf("%d", &G[i][j]);
    for (int i = 1; i <= n; i++)
        dis[i] = G[1][i];
    int MST = Prim(n, m);
    printf("%d\n", MST);
    system("pause");
    return 0;
}