并查集的路径压缩

【概述】

在并查集的寻找结点 x 的根结点的过程中，是不停的通过 father[] 数组去向上寻找其根结点

void Find (int x) { //递归实现
    if (father[x] != x) //x不是集合的代表时
        return Find(father[x]); //以当前结点的父结点进一步查询
    return father[x];
}

在这个过程中，相当于把结点 x 到其根结点的这条路径上的所有结点都遍历了一遍，而之后每次要查询这条路径上某结点的根结点，都要重新进行遍历，这无疑增大了时间复杂度

为减少时间复杂度，有了并查集中最重要的优化——路径压缩

在经过路径压缩后，再次查询该条路径上的根结点时，只需要 $O(1)$ 的复杂度即可得到根结点

【基本思想】

路径压缩的本质，是减少树的层数

在并查集中，对于一个结点来说，其父结点是哪个结点与其根结点是哪个结点毫无关系，每次都要一层层的找太浪费时间

因此，路径压缩，就是令路径上的每个结点，都直接连接到根结点上，这样以后在查询时，通过 father[i] 即可知道 i 号结点的根结点是谁

int Find (int x) { //路径压缩实现
    if (father[x] != x) //x不是集合的代表时
        return father[x] = Find(father[x]); //查找x的祖先找到代表，并路径压缩
    return father[x];
}

【实例】

假设初始并查集如下图

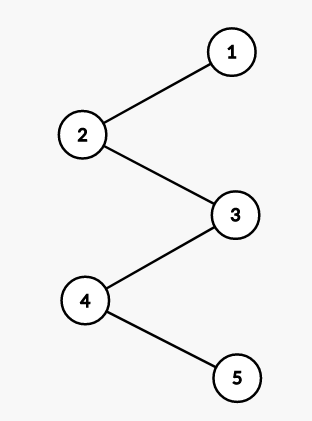
此时，father[] 数组如下：

• father[1]=1
• father[2]=1
• father[3]=2
• father[4]=3
• father[5]=4

在未经过路径压缩前，假设要进行 Find(4) 操作，那么，根据上述的路径压缩的 Find() 过程有：

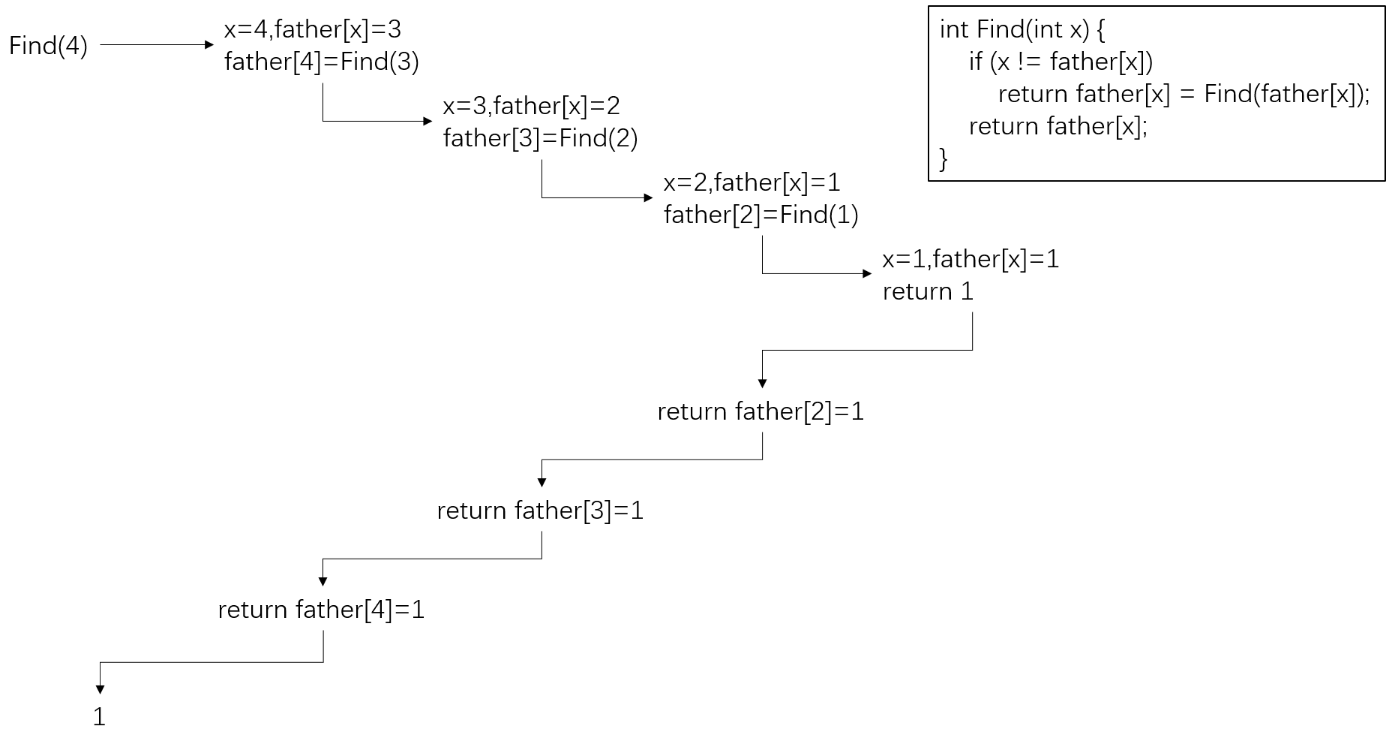
可以看出，在路径压缩完成后，有：

• father[1]=1
• father[2]=1
• father[3]=1
• father[4]=1
• father[5]=4

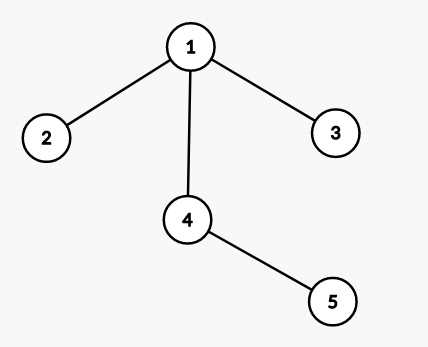
这样，当下一次 $1$ 号点到 $4$ 号点的路径时，只需要经过一次询问，即可得到相应结点的根结点