【概述】

并查集（Union-Find Set）是一种用于分离集合操作的抽象数据类型，其处理的是集合（set）之间的合并及查询问题

在并查集中，借助一个数组 father[] 来表示每个结点的父结点，即 father[i] 存储结点 i 的父结点编号

最主要的两种操作为：

查找（Find）：确定元素 a 的根结点
合并（Union）：将子集 a、b 合并为一个集合

当遇到有关物与物之间的关系，且这种关系是可传递的问题时，可以优先尝试用并查集解决

【基本操作】

初始化

在最开始时，所有的元素各自单独构成一个集合，当集合中只有一元素时，这个集合的代表结点即为该元素，即该元素的父结点（father）是其自身

因此并查集的初始化，即将每个元素作为自己的根结点

int father[N]; //father[i]存储结点i的父结点编号
void init (int n) {
    for (int i = 1; i <= n; i++)
        father[i] = i;
}

查询根结点编号

查询根结点编号，即给出一个元素编号 x 时，寻找到元素 x 的根结点的编号

以下图为例，假设我们要找 $6$ 号结点的根结点，那么过程为：首先找到 $6$ 号点的父结点为 $3$ 号，然后再找 $3$ 号的父结点为 $1$ 号，再找 $1$ 号的父结点为 $1$ 号，此时发现 $1$ 号点父结点是其自身，即满足 father[root]=root，说明找到了 $6$ 号点的根结点为 1 号点

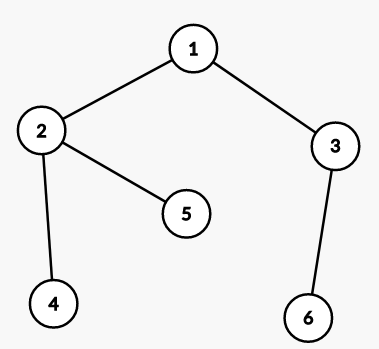
因此，我们利用 while 循环，非递归地实现查询根结点编号的操作操作

void Find (int x) { //非递归实现
    while (father[x] != x) //未查询到根结点时
        x = father[x]; //将当前结点更新为其根结点，继续向上寻找
    return x;
}

考虑到并查集中每个集合都是一棵树，那么可以借助树的递归性来完成上述操作

void Find (int x) { //递归实现
    if (father[x] != x) //未查询到根结点时
        return Find(father[x]); //以当前结点的父结点进一步查询
    return father[x];
}

合并两集合

对于两个不相交的集合，若想将这两个集合进行合并，并不需要在意祖先究竟是谁，只需要将一个集合中的祖先作为另一个集合祖先的孩子结点即可

对于分属两个集合中的元素 x、y，首先利用查找操作 Find()，找到这两个结点的根结点 fx、fy

若 fx == fy，说明两结点已经在同一个集合中，不需合并
若 fx != fy，说明两结点不再同一个集合中，将元素 y 的根结点 fy 作为 x 的根结点 fx 的儿子即可

void Union (int x,int y) {
    int fx = Find(x); //x的根结点
    int fy = Find(y); //y的根结点
    if (fx != fy) //判断fx与fy是否为一个根结点
        father[fy] = fx;
}

判断两元素是否属于同一集合

对于两个元素 x、y 来说，若想判断这两个元素是否为一个集合，只需要利用 Find() 来寻找他们的父结点 fx、fy

若 fx == fy，说明两元素根结点相同，为同一集合
若 fx != fy，说明两元素根结点不同，不为同一集合

bool judge (int x, int y) {
    int fx = Find(x); //x的根结点
    int fy = Find(y); //y的根结点
    if (fx == fy)
        return true;
    return false;
}

统计集合数目

在初始化后，每个元素都将自己作为自己的根结点

因此当需要统计并查集中的集合数目时，只需要统计有多少个元素的根结点是其自身即可

int countSets (int n) {
    int cnt = 0;
    for (int i = 1; i <= n; i++)
        if (father[i] == i)
            cnt++;
	return cnt;
}

统计每个集合中元素个数

统计每个集合中元素的个数需要两步：

对于 $n$ 个结点，先寻找他们的根结点，利用桶排的思想，来统计以 $i$ 为根结点时，该子集中的结点个数
统计根结点外的点，即对于每个元素，将其个数记为其根结点下的元素个数

int num[N]; //num[i]代表以i为根结点时，该子集下的元素数目
void countElements() {
    for (int i = 1; i <= n; i++) {
        father[i] = Find(i); //寻找每个节点的根结点
        num[father[i]]++;    //统计根结点下的节点个数
    }
    for (int i = 1; i <= n; i++) //统计根节点外的点的个数
        num[i] = num[father[i]]; //对于每个元素，将其个数记为其根结点下的元素个数
}

【时空复杂度】

阿克曼函数

阿克曼函数（Ackermann），是一个非原始递归函数，其输出值增长速度很快

阿克曼函数被定义为：

$A(m,n)=\left\{\begin{matrix} n+1, & m=0 \\ A(m-1,1), & m>0,n=0 \\ A(m-1,A(m,n-1)), & otherwise \end{matrix}\right.$

阿克曼函数的单变量反函数 $\alpha(n)$ 被称为反阿克曼函数，其被定义为：最大的整数 $m$，使得 $A(m,m)\leq n$ 成立

阿克曼函数 $A(m,n)$ 的增长速度极快，但反阿克曼函数 $\alpha(n)$ 增长速度很慢，它们常出现在算法时间复杂度分析中

时间复杂度

在本文中所论述的并查集，是最基础的并查集，没有进行任何优化

但在实际应用中，可以对并查集进行路径压缩和启发式合并优化，此时的并查集的时间复杂度常用反阿克曼函数 $\alpha(n)$ 来衡量

在同时使用路径优化和启发式合并后，并查集的每个操作平均时间为：

$O(\alpha(n))$

通常，在 OI&ACM 竞赛中，即使不适用启发式合并，代码也往往能在规定时间内完成任务

在 Tarjan 的论文[1]中，证明了不使用启发式合并、只使用路径压缩的最坏时间复杂度为：

$O(m\log n)$

在姚期智的论文[2]中，证明了不使用启发式合并、只使用路径压缩的平均时间复杂度为：

$O(m\alpha(m,n))$

空间复杂度

显然，并查集的空间复杂度为：

$O(n)$

References

[1]Tarjan, R. E., & Van Leeuwen, J. (1984). Worst-case analysis of set union algorithms. Journal of the ACM (JACM), 31(2), 245-281.ResearchGate PDF

[2]Yao, A. C. (1985). On the expected performance of path compression algorithms.SIAM Journal on Computing, 14(1), 129-133.

Alex_McAvoy

并查集及其基本操作