数组与矩阵的压缩存储

【数组】

概念

数组，是由 $n(n \geq1 )$ 个相同类型的数据元素构成的有限序列，每个数据元素被称为一个数组元素，每个元素在数组中的序号称为数组的下标，下标的取值范围被称为维界

其是数组是线性表的推广，但与线性表不同是，数组一旦被定义，维数和维界都不会再改变，因此数组除初始化和销毁外，只有存取和修改操作

也就是说，对于一维数组来说，可视为定长线性表，对于二维数组来说，可视为元素定长线性表的定长线性表

存储结构

一个数组的所有元素在内存中占据一段连续的存储空间

对于一维数组 $a[0,1,…,n-1]$ 来说，设每个数组元素所占的存储空间为 $L$

则第 $i$ 个元素 $a_i$ 的地址为：

$$LOC(a_i)=LOC(a_0)+i*L,\quad 0 \leq i<n$$

对于二维数组 $a[0,1,…,n-1][0,1,…,m-1]$ 来说，设每个数组元素所占的存储空间为 $L$，其有两种映射方法

若按行优先存储，则第 $i$ 行第 $j$ 个元素 $a_{ij}$ 的地址为：

$$LOC(a_{ij})=LOC(a_{00})+(i*m+j)*L$$

若按列优先存储，则第 $i$ 行第 $j$ 个元素 $a_{ij}$ 的地址为：

$$LOC(a_{ij})=LOC(a_{00})+(j*n+i)*L$$

【矩阵的压缩存储】

概述

矩阵在计算机图形学、工程计算中十分重要，在数据结构中，考虑的是如何用最小的内存空间来存储矩阵

由于矩阵中存在诸多元素，为此在矩阵的特性上对矩阵存储进行入手，最基本的方法即压缩存储，其将多个值相同的元素分配到同一个存储空间，对零元素不分配存储空间

而对于常见的对称矩阵、上下三角矩阵、对角矩阵等特殊矩阵，其压缩存储的方法是根据其元素分布规律找出存储方案，将呈现规律性分布的值相同的多个矩阵元素压缩存储到一个元素空间中

矩阵可以划分为如下图所示的三个区域

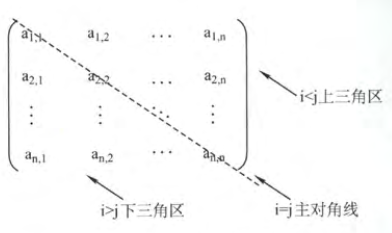
对称矩阵

对于一个 $n$ 阶方阵 $A[0…n][0…n]$，若对其中任意元素 $a_{ij}$，都有 $a_{ij}=a_{ji}$ 成立，则称该方阵为对称矩阵

对于对称矩阵来说，上三角区所有元素与下三角区所有元素相同，若仍采用二维数组存放，则会浪费一半的存储空间

为此，对称矩阵的存储方式是：只存放含主对角线元素的下三角元素区域

具体来说，对于对称矩阵 $A[1…n][1…n]$ 将会存放到数组下标从 $0$ 开始的一维数组 $B[\frac{n(n+1)}{2}]$ 中

而当 $i\geq j$ 时，数组 $B$ 中位于元素 $a_{ij}$ 前的元素为：

第一行：$1$ 个元素，$a_{11}$

第二行：$2$ 个元素，$a_{21},a_{22}$

$……$

第 $i-1$ 行：$i-1$ 个元素，$a_{i-1,1},a_{i-1,2},…,a_{i-1,i-1}$

第 $i$ 行：$j-1$ 个元素，$a_{i,1},a_{i,2},…,a_{i,j-1}$

即元素 $a_{ij}$ 在数组 $B$ 的下标 $k$ 满足：

$$k=1+2+...+(i-1)+j-1=\frac{i(i-1)}{2}+j-1$$

那么，元素 $a_{ij}$ 的下标与数组 $B$ 的下标对应关系为：

$$k=\left\{\begin{matrix} \frac{i(i-1)}{2}+j-1, &i\geq j(下三角与主对角线)\\ \frac{j(j-1)}{2}+i-1,&i<j(上三角) \end{matrix}\right.$$

下三角矩阵

在下三角矩阵中，上三角区元素均为同一常量，因此其存储思想与对称矩阵类似，在存储完下三角区域和主对角元素后，接着存储对角线上方元素一次即可

也就是说，可以将下三角矩阵 $A[1…n][1…n]$ 存放到数组下标从 $0$ 开始的一维数组 $B[\frac{n(n+1)}{2}+1]$ 中

元素 $a_{ij}$ 的下标与数组 $B$ 的下标对应关系为：

$$k=\left\{\begin{matrix} \frac{i(i-1)}{2}+j-1,& i\geq j（(三角与主对角线)\\ \frac{n(n+1)}{2},& i<j (上三角) \end{matrix}\right.$$

下三角矩阵元素在内存中的压缩存储形式如下图

上三角矩阵

在上三角矩阵中，下三角区元素均为同一常量，因此只需要存储上三角区元素、主对角、下三角区元素常量一次

也就是说，可以将下三角矩阵 $A[1…n][1…n]$ 存放到数组下标从 $0$ 开始的一维数组 $B[\frac{n(n+1)}{2}+1]$ 中

当 $i\leq j$ 时，数组 $B$ 中位于元素 $a_{ij}$ 前的元素个数为：

第一行：$n$ 个元素

第二行：$n-1$ 个元素

$……$

第 $i-1$ 行：$n-i+2$ 个元素

第 $i$ 行：$j-i$ 个元素

即元素 $a_{ij}$ 在数组 $B$ 的下标 $k$ 满足：

$$k=n+(n-1)+...+(n-i+2)+(j-i)=\frac{(i-1)(2n-i+2)}{2}+j-i$$

那么，元素 $a_{ij}$ 的下标与数组 $B$ 的下标对应关系为：

$$k= \left\{\begin{matrix} \frac{(i-1)(2n-i+2)}{2}+(j-i),& i\leq j(上三角与主对角线)\\ \frac{n(n-1)}{2},&i>j(下三角) \end{matrix}\right.$$

上三角矩阵元素在内存中的压缩存储形式如下图

三对角矩阵

对于 $n$ 阶方阵 $A$ 中的任一元素 $a_{ij}$，当 $|i-j|>1$ 时，若有 $a_{ij}=0$，则称该方阵为三对角矩阵，其所有非零元素均集中在以主对角线为中心的三条对角线区域中，其他区域元素均为 $0$

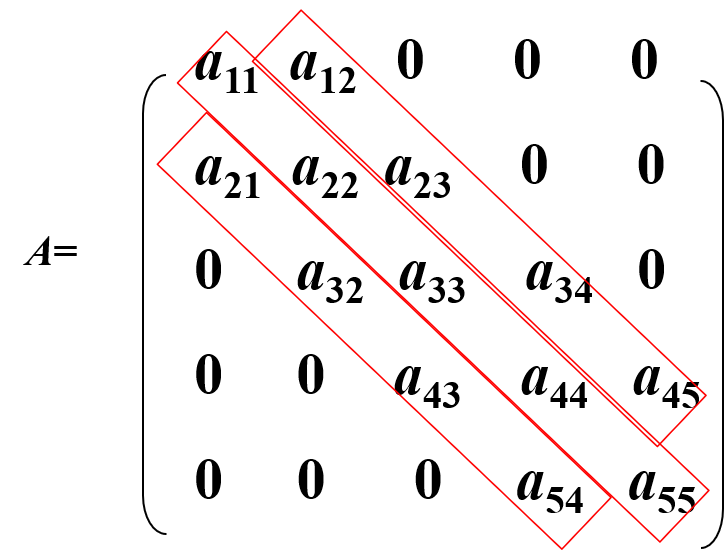
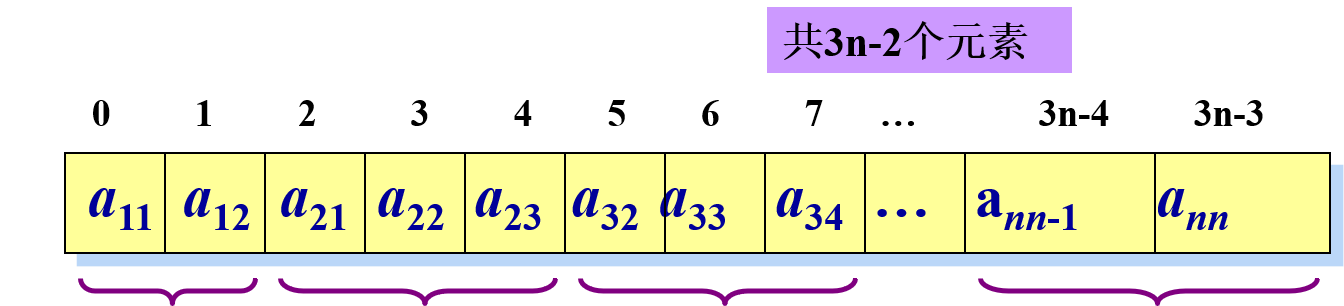
三对角矩阵的压缩存储方式是：将三条对角线元素按行优先存放在一维数组 $B$ 中，元素 $a_{ij}$ 对应 $B$ 中下标 $k=2i+j-3$

反之，若已知某元素 $a_{ij}$ 处存放在第 $k$ 个位置，则有：

$$\left\{\begin{matrix} i=\lfloor\frac{k+1}{3}+1\rfloor\\ j=k-2i+3 \end{matrix}\right.$$

稀疏矩阵

假设矩阵元素的个数为 $s$ ，当矩阵中的非零元素个数 $t$ 远远小于 $s$，即 $t<<s$ 时，该矩阵被称为稀疏矩阵

稀疏矩阵通常的存储方式是：将非零元素、行、列构建成一个三元组 (行标，列标，值)，再利用数组或链表存储所有三元组

这样一来，虽然能用较小的空间来存储较大的稀疏矩阵，但却失去了随机存储的特性