【基本思想】

快速排序对冒泡排序的一种改进，在冒泡排序中，记录的比较与移动是在相邻位置进行的，记录每次交换只能后移一个位置，因而总的比较次数与移动次数较多；而在快速排序中，记录的比较与移动是从两端向中间进行的，关键码较大的记录一次就能从前面移动到后面，关键码较小的记录一次就能从后面移动到前面，由于记录移动的距离较远，从而减少了总的比较次数与移动次数

快速排序利用了分治策略，其基本思想是：首先选一个轴值，作为比较的基准，将待排序记录划分为独立的两部分，左侧记录均小于等于轴值，右侧记录均大于等于轴值，然后分别对这两部分重复上述过程，直至序列有序

其宏观排序过程如下图

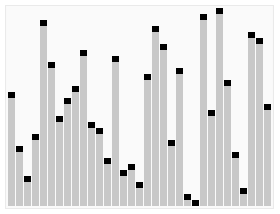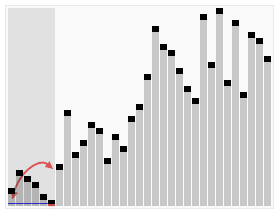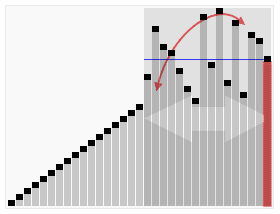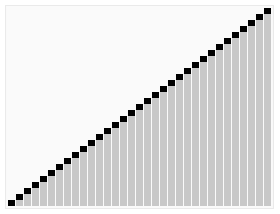
【算法步骤】

显然，快速排序是一个递归的过程，其算法步骤为：

1）在待排序的 $n$ 个记录中任选一个记录作为轴值（通常选第 $1$个）

2）进行分区，设置两个指针 $i$、$j$，初值分别为 $left$、$right$

指针 $j$ 以 $right$ 为起点，从后向前搜索第一个小于轴值的元素，将其交换到指针 $i$ 所指的元素
指针 $i$ 从 $left$ 为起点，从前向后搜索第一个大于轴值的元素，将其交换到指针 $j$ 所指的元素

当指针 $i=j$ 时，指针 $i$ 之前的元素均小于等于轴值，指针 $i$ 之后的元素均大于等于轴值

3）对左右两个分区递归的进行上述步骤，直到子序列大小为 $1$

【实例】

以数列 $\{49,38,65,97,76,13,27,49\}$ 为例，演示快速排序过程：

初始时，选取轴值为 $49$，第一次分区过程如下：

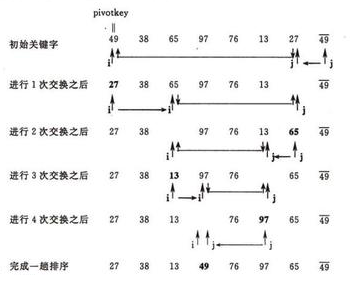
之后的每一趟，对左右分区递归的选取轴值，进行排序：

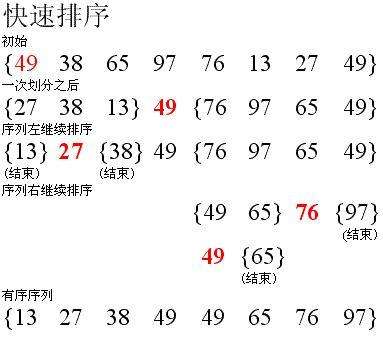
可以看出，快速排序的阶段性排序结果的特点是：第 $i$ 趟完成时，会有 $i$ 个以上的数出现在它最终将要出现的位置，即其左边的数都比他小，右边的数都比他大

【性能分析】

快速排序仅适用于顺序存储结构，在划分算法中，若右端区间有两个关键字相同，且均小于轴值，则在交换到左区间后，它们的相对位置会发生变化，因此其是一种不稳定排序算法

由于快速排序是递归进行的，其需要借助一个递归工作栈来保存每层递归调用的信息，其容量与递归调用最大深度一致，最好情况时空间复杂度为 $O(log_2n)$，最坏情况时要进行 $n-1$ 次递归，空间复杂度为 $O(n)$，平均情况下空间复杂度为 $O(log_2n)$

快速排序的时间复杂度与划分是否对称有关，最坏情况发生在两区域分别包含 $n-1$ 个元素和 $0$ 个元素时，此时这种最大程度的不对称若发生在每层递归上，即对应初始排序表基本有序或基本逆序时，时间复杂度为 $O(n^2)$

为避免快速排序出现最坏的情况，一般是从序列的头尾和中间各选一个元素，然后再取这三个元素中的中值作为轴值，以避免最坏情况的发生

在理想的状态下，可能做到最平衡的划分，得到的两个子问题的大小都不可能大于 $\frac{n}{2}$，在这种情况下，快速排序的最好时间复杂度与平均时间复杂度均为 $O(nlog_2n)$

快速排序是所有内部排序算法中平均性能最优的排序算法

【实现】

快速排序的关键在于划分操作，其性能也取决于划分操作的好坏，对于最基础的快速排序，每次总选择当前表中第一个元素作为轴值来对表进行划分，将表中比轴值小的元素向左移动，比轴值大的元素向右移动

int partitoin (int a[], int left, int right) {
    int pivotKey = a[left];  //轴值
    int i = left, j = right; //左右指针
    while (i < j) {
        while (i < j && a[j] >= pivotKey) //右侧扫描
            j--;
        swap(a[i], a[j]); //比轴值小的交换到低端
        while (i < j && a[i] <= pivotKey) //左侧扫描
            i++;
        swap(a[i],a[j]); //比轴值大的交换到高端
    }
    return i; //返回轴值所在位置
}

在每次划分操作结束后，得到轴值所在位置，之后对表的左右两端递归的进行快速排序即可

初始时，调用 quickSort(a, 1, n) 即可

void quickSort (int a[], int left, int right) {
    if (left < right) {
        int pivotKey = partitoin (a, left, right); //算出轴值并根据轴值进行分区
        quickSort(a, left, pivotKey - 1); //左子表递归
        quickSort(a, pivotKey + 1, right); //右子表递归
    }
}