【基本思想】

归并排序是分治策略的一个非常典型的应用，其基本思想是将 $n$ 个待排序的记录看成是 $n$ 个长度为 $1$ 的有序序列，然后两两进行归并，第一轮得到 $\frac{n}{2}$ 个长度为 $2$ 的有序序列，第二轮得到 $\frac{n}{4}$ 个长度为 $4$ 的有序序列，以此类推，直到得到一个长度为 $n$ 的有序序列

归并排序的核心是归并操作，即将两个已经排序的序列合并成一个序列的操作，其步骤如下：

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤 3 直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

其宏观排序过程如下图

【实例】

以数列 $\{8,5,3,1,8,7,2,4\}$ 为例，演示归并排序过程：

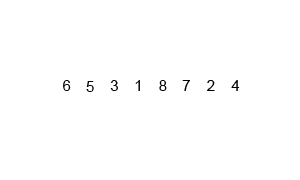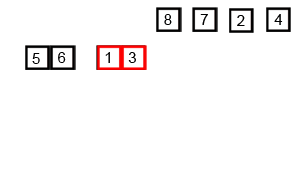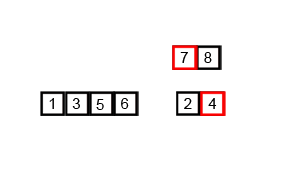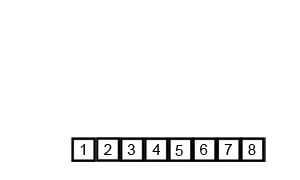
【性能分析】

归并排序适用于顺序存储方式，由于归并过程并不会改变相同关键字的相对次序，因此其是一种稳定排序算法

在归并过程中，需要 $n$ 个辅助空间，因此其空间复杂度为：

$O(n)$

每趟归并的时间复杂度为 $O(n)$，需要进行 $\left \lceil log_2n\rceil \right.$ 趟归并，总时间复杂度为：

$O(nlog_2n)$

【实现】

归并操作

归并操作是核心操作，通过对归并操作的递归调用，即可完成归并排序

void mergeArray (int a[], int left, int mid, int right, int temp[]) {
    int i = left, j = mid + 1;
    int cnt = 0; //临时数组temp的指针

    while (i <= mid && j <= right) { //比较左右两个子序列
        if (a[i] <= a[j]) //取a[i]与a[j]中的小者放入temp[k]
            temp[cnt++] = a[i++];
        else
            temp[cnt++] = a[j++];
    }
    while (i <= mid) //第一个子序列未处理完
        temp[k++] = a[i++];
    while (j <= right) //第二个子序列未处理完
        temp[k++] = a[j++];
 
    for(int i = 0; i < k; i++) //将数组temp中的值返回数组a
        a[left+i] = temp[i];
}

递归调用

void mergeSort (int a[], int left, int right, int temp[]) {
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort (a, left, mid, temp);    //左边有序
        mergeSort (a, mid+1, right, temp); //右边有序
        mergeArray (a, left, mid, right, temp); //将两个有序数列合并
    }
}