【基本思想】

计数排序是非比较类排序一种，其基本思想是：对于给定的输入序列中的每一个元素 $x$，确定该序列中值小于 $x$ 的元素的个数，一旦有了这个信息，就可以将 $x$ 直接存放到最终的输出序列的正确位置上

例如，如果输入序列中只有 $17$ 个元素的值小于 $x$ 的值，则 $x$ 可以直接存放在输出序列的第 $18$ 个位置上

当然，如果有多个元素具有相同的值时，不能将这些元素放在输出序列的同一个位置上

计数排序的排序过程为：

统计数组中每个值为 $i$ 的元素出现的次数，存入数组 $C$ 的第 $i$ 项
求每个数出现次数的前缀和，即数组 $C$ 的前缀和
根据出现次数的前缀和，从右向左反向计算每个数的位置，即将每个元素 $i$ 放在新数组的第 $C[i]$项，同时，每放一个元素就将 $C[i]$减去 $1$

【实例】

以数列 $\{0,2,5,3,7,9,10,3,7,6\}$ 为例，演示计数排序的过程

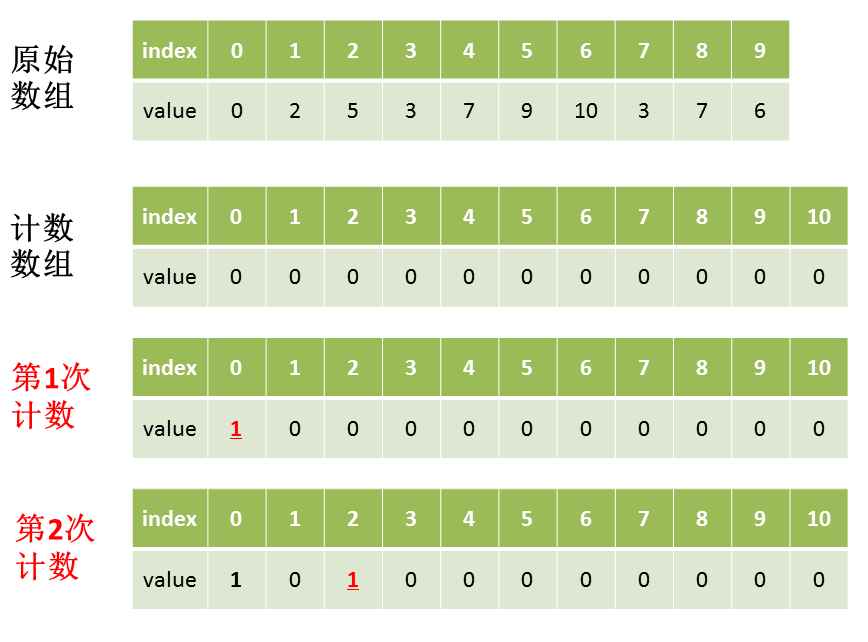
【性能分析】

计数排序适用于顺序存储结构，在计数累加过程中，并没有改变相同元素的相对位置，因此其是一种稳定排序算法

计数排序需要一个用来暂存输出序列的数组，其大小与输入序列大小相同，此外，还需要一个来暂存每个数出现次数的前缀和的数组，因此，其空间复杂度为：

$O(n)$

计数排序的时间复杂度大小与待排序数据的值域大小有关，假设值域大小为 $w$，那么时间复杂度为：

$O(n+w)$

【实现】

#define MAXNUM 20 //待排序数的最大个数
#define MAX 100   //待排序数的最大值
int res[MAXNUM];
int temp[MAX+1];

void countSort (int a[], int n) {
    for (int i = 0; i < n; i++) //统计i的次数
        temp[a[i]]++;

    for (int i = 1; i <= MAX; i++) //对所有的计数累加，统计数组a的前缀和与小于小于a数组值出现的个数
        temp[i]+=temp[i-1];

    for (int i = n - 1; i >= 0; i--) { //逆向遍历源数组，根据计数数组中对应的值填充到新数组中
        res[temp[a[i]]-1] = a[i]; //temp[a[i]]表示数组a中包括a[i]和小于a[i]的总数
        temp[a[i]]--; //如果数组a中有相同的数，a[i]的下标-1
    }
}