【基本思想】

基数排序借助多关键字排序的思想，对单逻辑关键字进行排序，简单来说，其是基于关键字各位的大小进行排序

假设长度为 $n$ 的线性表中每个结点 $a_j$ 的关键字由 $d$ 元组 $(k_j^{d_-1},k_j^{d_-2},…,d_j^1,d_j^0)$ 组成，满足 $0\leq k_j^i\leq r-1$，其中 $k_j^{d-1}$ 为最主关键字，$k_j^0$ 为最次关键字，且 $0\leq j <n,0\leq i\leq d-1$

为实现多关键字排序，有两种方法：

最高位优先（MSD）：按关键字位权重递减，逐层划分为若干更小子序列，最后将所有子序列连接成有序序列
最低位优先（LSD）：按关键字位权重递增，逐层划分为若干更小子序列，最后将所有子序列连接成有序序列

以 $r$ 为基数的最低位优先基数排序为例，其实现过程为：

设置 $r$ 个辅助队列 $Q_0,Q_1,…,Q_{r-1}$
对 $i=0,1,…,d-1$，依次进行分配和收集
分配：将 $Q_0,Q_1,…,Q_{r-1}$ 设为空队列，依次考察表中每个结点 $a_j$，若 $a_j$ 的关键字 $k_j^i=k$，则将 $a_j$ 放入队列 $Q_k$ 中
收集：将 $Q_0,Q_1,…,Q_{r-1}$ 中的结点依次首尾连接，得到新的结点序列，从而组成新的线性表

【实例】

以 $\{278,109,063,930,589,184,505,269,8,83\}$ 为例

每个关键字均为 $1000$ 以下的正整数，基数 $r=10$，每个关键字由 $K^1K^2K^3$ 构成，分别代表百位、十位、个位，共需进行三趟分配、收集

第一趟：用最低子关键字 $K^3$ 进行，将所有最低子关键字相等的记录分配到同一队列，然后进行收集

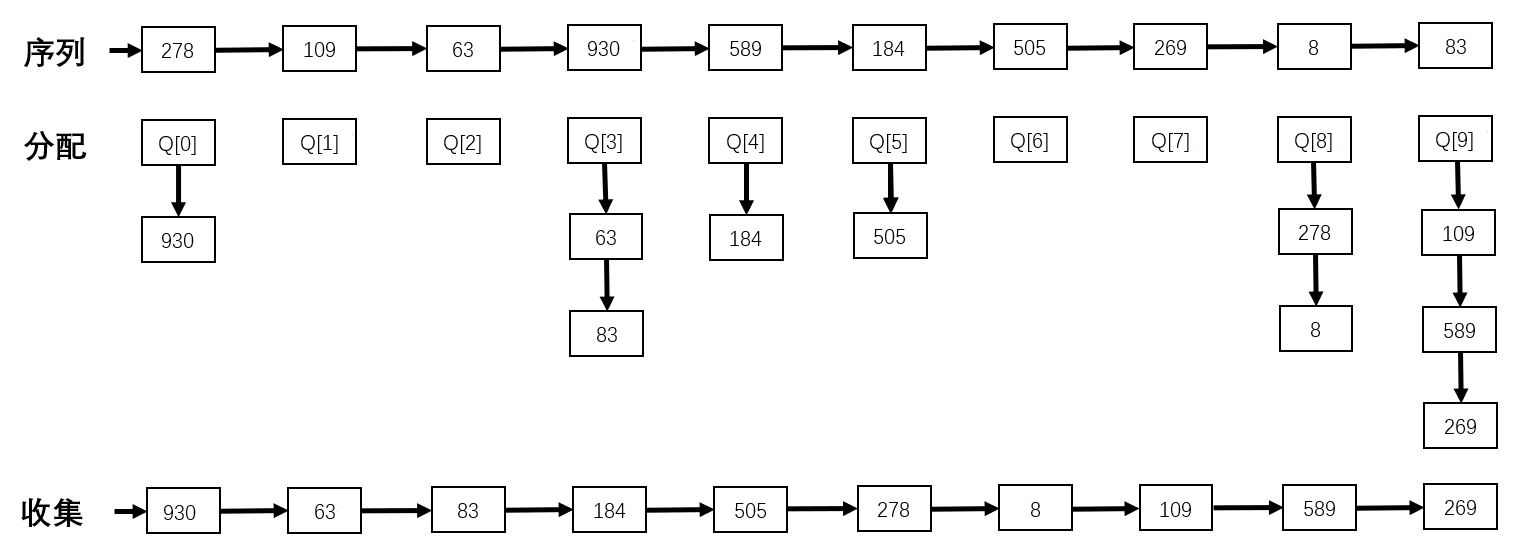
第二趟：用次低子关键字 $K^2$ 进行，将所有次低子关键字相等的记录分配到同一队列，然后进行收集

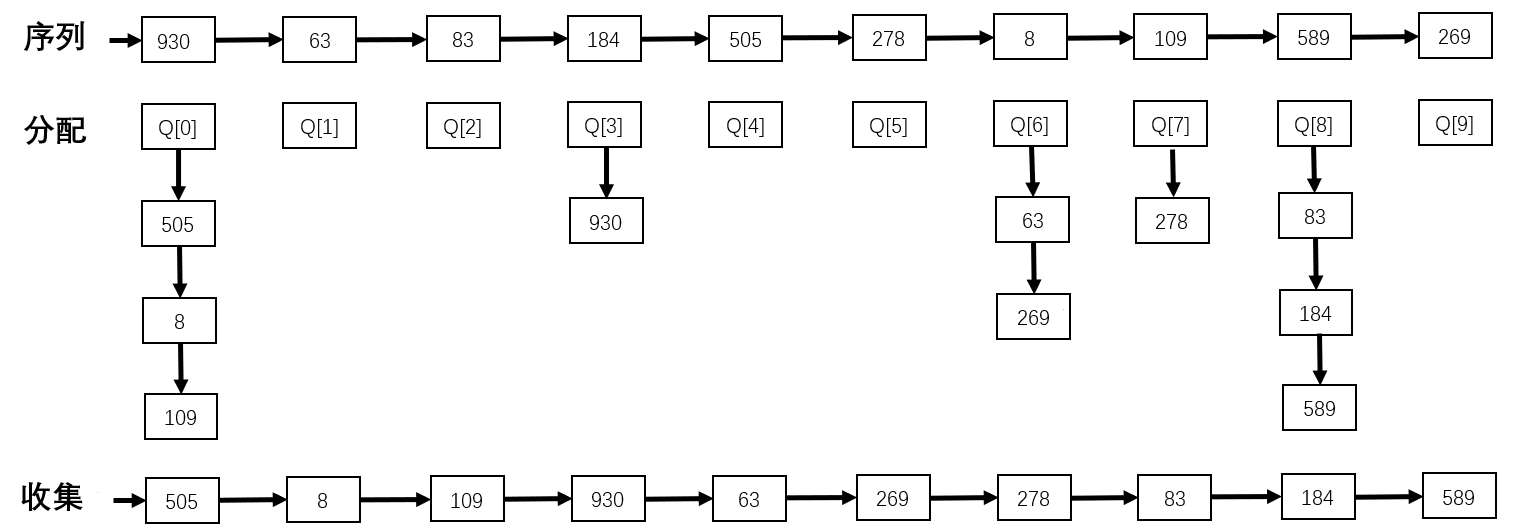
第三趟：用最高子关键字 $K^1$ 进行，将所有最高子关键字相等的记录分配到同一队列，然后进行收集

至此，排序结束

【性能分析】

基数排序适用于顺序存储、链式存储结构，由于队列先进先出的特性，分配与收集过程中并不会改变相同关键字的相对次序，因此其是一种稳定排序算法

对于链式存储结构来说，每一趟需要 $r$ 个队列，之后的排序会重复利用这些队列，因此其空间复杂度为：

$O(r)$

时间复杂度与序列初始状态无关，由于每一趟分配的时间复杂度为 $O(n)$，每一趟收集的时间复杂度为 $O(r)$，总共需要 $d$ 趟分配与收集，因此，总时间复杂度为：

$O(d(n+r))$

【实现】

#define RADIX 10  //基数为10,需要十个桶
#define KEYNUM 10 //关键字位数，这里为整型位数
int getDigitInPos(int num, int pos) { //找到数字num的从第到高的第pos位数据
    int temp = 1;
    for (int i = 0; i < pos - 1; i++)
        temp *= 10;
    return (num / temp) % 10;
}
void radixSort (int a[], int n) {
    int *b[RADIX]; //分别为0~9基数的存放空间  
    for (int i = 0; i < 10; i++) {
        b[i] = (int *)malloc(sizeof(int)*(dataNum + 1));
        b[i][0] = 0; //index为0处记录这组数据的个数
    }
    for (int pos = 1; pos <= KEYNUM; pos++) {//从个位开始入桶并出桶
        for (int i = 0; i < n; i++) { //分配
            int num = getDigitInPos(a[i], pos);
            int index = ++b[num][0];
            b[num][index] = a[i];
        }
        for (int i = 0, j = 0; i < RADIX; i++){ //收集
            for (int k = 1; k <= radixArrays[i][0]; k++)
                a[j++] = b[i][k];
            b[i][0] = 0;//出桶完毕，复位  
        }  
    }  
}