【随机变量的产生】

matlab 中产生随机数的函数有很多，除了特殊矩阵中提到的用于生成测试矩阵的函数外，还有一些可生成常见分布的随机数产生函数

对于常用的二项分布的随机数据的产生，有：

binornd(N,P)：产生服从 N、P 的二项分布随机数
binornd(N,P,m,n)：产生服从 N、P 的二项分布随机数 R，m、n 用于指定 R 的行数和列数
binornd(N,P,[m,n])：产生服从 N、P 的二项分布随机数 R，m、n 用于指定 R 的行数和列数

>> n=10:10:50;
>> p=1./n;
>> binornd(n,p)
ans = 3     2     2     0     2
>> binornd([n;n],[p;p])
ans =
     1     1     0     0     0
     0     1     0     1     3
>> binornd(10,100,2,5)
ans =
   NaN   NaN   NaN   NaN   NaN
   NaN   NaN   NaN   NaN   NaN

除二项分布外，常见随机数产生函数表如下，他们的用法均于上述的二项分布的随机数据的产生相同：

函数	说明
binornd	产生服从 N、P 的二项分布随机数
normrnd	产生服从 mu、sigma 的正态分布随机数
unifrnd	产生 [a,b] 上均匀分布且连续的随机数
unidrnd	产生均匀分布且离散的随机数
exprnd	产生服从 Lambda 的指数分布随机数
poissrnd	产生服从 Lambda 的泊松分布随机数
chi2rnd	产生自由度为 n 的卡方分布随机数
trnd	产生自由度为 n 的 t 分布随机数
frnd	产生第一自由度为 N1，第二自由度为 N2 的 F 分布随机数
gamrnd	产生参数为 a、b 的伽马分布随机数
betarnd	产生参数为 a、b 的贝塔分布随机数
lognrnd	产生参数为 mu、sigma 的对数正态分布随机数
nbinrnd	产生参数为 r、p 的负二项式分布随机数
ncfrnd	产生参数为 n1、n2、delta 的非中心 F 分布随机数
nctrnd	产生参数为 n、delta 的非中心 t 分布随机数
ncx2rnd	产生参数为 n、delta 的非中心 t 卡方分布随机数
raylrnd	产生参数为 b 的瑞利分布随机数
weibrnd	产生参数为 a、b 的韦伯分布随机数
geornd	产生参数为 p 的几何分布随机数
hygernd	产生参数为 M、K、N 的超几何分布随机数

【概率密度】

通用函数概率密度

pdf(name,X,A)：返回 x=X 处，参数为 A 的概率密度值
pdf(name,X,A,B)：返回 x=X 处，参数为 A、B 的概率密度值
pdf(name,X,A,B,C)：返回 x=X 处，参数为 A、B、C 的概率密度值

注：

关于参数 A、B、C：根据不同的分布，参数个数不同
关于 name：用于指定是何种分布，常见取值见下表

取值	说明	取值	说明
beta	beta分布	bino	二项分布
chi2	卡方分布	exp	指数分布
f	F分布	gam	伽马分布
geo	几何分布	hyge	超几何分布
logn	对数分布	norm	正态分布
poiss	泊松分布	rayl	瑞利分布
t	t分布	unif	均匀分布
unid	离散均匀分布

1
2
3

>> pdf('normal',-5:5,0,1)
ans =
    0.0000    0.0001    0.0044    0.0540    0.2420    0.3989    0.2420    0.0540    0.0044    0.0001    0.0000

此外，通用函数计算概率密度可以推广到任意函数、数据的情况

[f,Xi]=ksdensity(x)：对于待统计的向量 x，计算概率密度的点 Xi 与概率密度 f
f=ksdensity(x,Xi)：对于待统计的向量 x 和概率密度的点 Xi，计算概率密度 f

>> x=randn(10000,1);
>> fx=sin(x*pi);
>> [f,Xi]=ksdensity(fx);
>> figure
>> plot(Xi,f)
>> axis tight

专用函数概率密度

专用函数概率密度，是 matlab 中封装好的用于计算特定分布的概率密度的函数

以计算二项分布的概率密度函数为例，其余的函数调用方法与之类似：

binopdf(X,n,p)：计算实验次数为 n，每次实验中事件发生概率为 p 在 x=X 处的概率密度值

专用函数概率密度函数表如下：

调用格式	说明
unifpdf(x,a,b)	计算[a,b]上连续概率密度在X=x处的概率密度函数值
unidpdf(x,n)	计算离散概率密度函数值
exppdf(x,lambda)	计算参数为 lambda 的指数分布概率密度函数值
normpdf(x,mu,sigma)	计算参数为 mu、simga 的正态分布概率密度函数值
chi2pdf(x,n)	计算自由度为 n 的卡方分布概率密度函数值
tpdf(x,n)	计算自由度为 n 的 t 分布概率密度函数值
fpdf(x,n1,n2)	计算第一自由度为 n1，第二自由度为 n2 的 F 分布概率密度函数值
gampdf(x,a,b)	计算参数为 a、b 的伽马分布概率密度函数值
betapdf(x,a,b)	计算参数为 a、b 的贝塔分布概率密度函数值
lognpdf(x,mu,sigma)	计算参数为 mu、sigma 的对数正态分布概率密度函数值
ralypdf(x,b)	计算参数为 b 的瑞利分布概率密度函数值
geopdf(x,p)	计算参数为 p 的几何分布概率密度函数值
hygepdf(x,m,k,n)	计算参数为 p 的超几何分布概率密度函数值
poisspdf(x,lambda)	计算参数为 lambda 的泊松分布概率密度函数值

实例：正态分布函数概率密度的计算

>> mu=[0:0.1:5];
>> [y,i]=max(normpdf(1.5,mu,1));
>> mle=mu(i)
mle = 1.5000

【累计概率分布】

通用函数累计概率

使用 cdf() 可以计算随机变量 $x\leq X$ 的概率之和

cdf(name,X,A)：返回 x=X 处，参数为 A 的累计概率
cdf(name,X,A,B)：返回 x=X 处，参数为 A、B 的累计概率
cdf(name,X,A,B,C)：返回 x=X 处，参数为 A、B、C 的累计概率

注：

关于参数 A、B、C：根据不同的分布，参数个数不同
关于 name：用于指定是何种分布，常见取值见上表

专用函数累计概率

专用函数累计概率的写法，与上表写法基本相同，不同的是将 pdf 换为了 cdf

例如：poisscdf(x,lambda)

由于用法相同，只是返回结果不同，故不再赘述

【统计特征】

mean(A)：求 A 的平均值
median(A)：求 A 的中位数
nanmedian(A)：忽略 NaN 求 A 的中位数
geomean(A)：求 A 的几何平均值
harmmean(A)：求 A 的调和平均值
var(A)：求 A 的方差
std(A)：求 A 的标准差
skewness(A)：求 A 的三阶统计量斜度
cov(A,B)：求 A 和 B 的协方差
corrcoef(A,B)：求 A 和 B 的皮尔逊相关系数

【统计作图】

正整数频率表

tabulate(A)：求 A 的正整数频率表

>> a=ceil(randn(1,5));
>> tabulate(a)
  Value    Count   Percent
     -2        1     20.00%
      1        3     60.00%
      2        1     20.00%

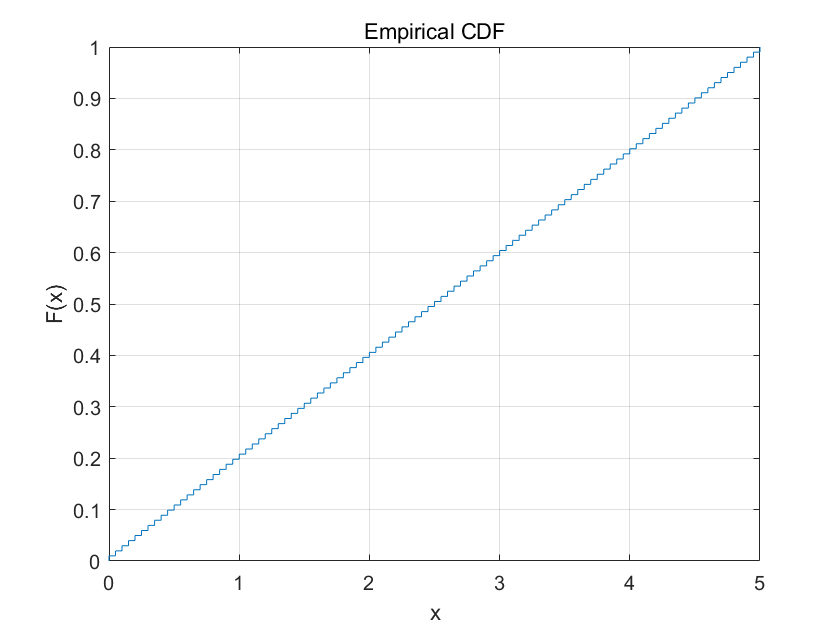
累积分布函数图形

cdfplot(a)：画出向量 a 的累积分布图形

1
2
3

>> x=0:0.05:5;
>> figure
>> cdfplot(x)

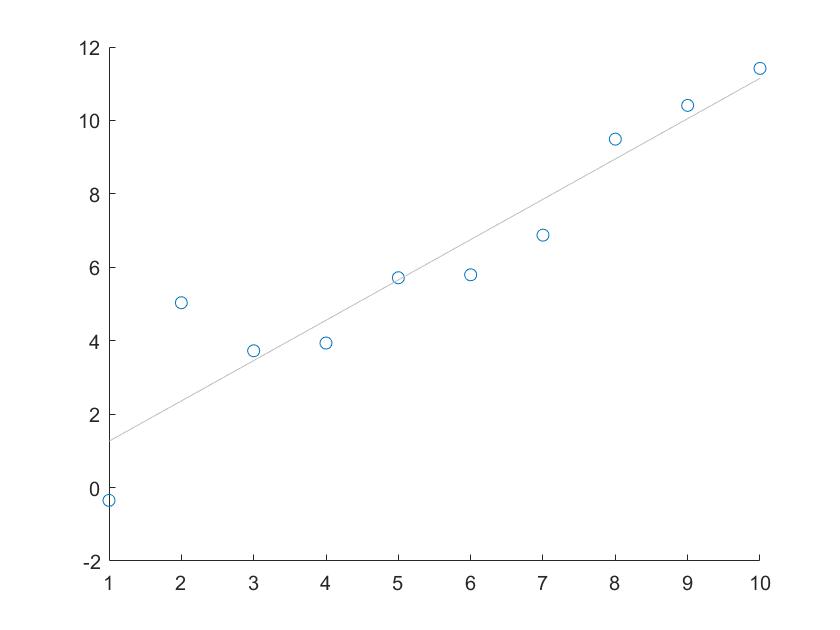
最小二乘拟合曲线

h=lsline：画出最小二乘拟合曲线

>> x=1:10;
>> y=x+randn(1,10);
>> figure
>> scatter(x,y)
>> lsline
>> h=lsline
h = 
  Line (lsline) (具有属性):
              Color: [0.7500 0.7500 0.7500]
          LineStyle: '-'
          LineWidth: 0.5000
             Marker: 'none'
         MarkerSize: 6
    MarkerFaceColor: 'none'
              XData: [1 10]
              YData: [1.2620 11.1478]
              ZData: [1x0 double]

正态分布概率图形

h=normplot(X)：绘制 X 的正态分布概率图形，若 X 为向量，则直接显示；若 X 为矩阵，则显示每一列的图形

>> x=1:10;
>> y=x+randn(1,10);
>> subplot(2,1,1)
>> normplot(y)
>> subplot(2,1,2)
>> x=magic(3);
>> normplot(x)

箱线图

boxplot(X)：绘制 X 的箱线图
boxplot(X,Y)：绘制变量为 X，附加群为 Y 的箱线图

>> x=1:10;
>> subplot(2,1,1)
>> boxplot(x)

>> subplot(2,1,2)
>> boxplot(x,1)

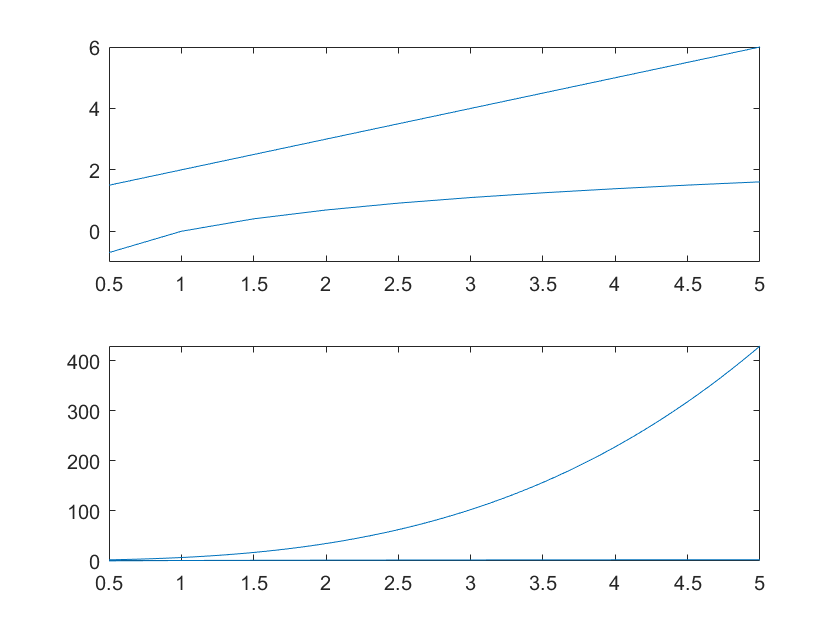
参考线

refline(k,b)：绘制斜率为 k，截距为 b 的参考直线
refcurve(p)：绘制参数为多项式系数的参考曲线

>> subplot(2,1,1)
>> x=0:0.5:5;
>> y=log(x);
>> plot(x,y)
>> refline(1,1)

>> subplot(2,1,2)
>> plot(x,y)
>> refcurve([3 2 1 0])

样本概率图形

p=capaplot(X,[a,b])：绘制参数为 X，范围为 [a,b] 的样本概率图形，并返回在范围内的概率

1
2
3

>> X=normrnd(1,0.05,300,1);
>> capaplot(X,[0.5,1.5])
ans = 1

正态拟合曲线图

histfit(X)：画出 X 的正态拟合曲线图
histfit(X,num)：画出 X 的正态拟合曲线图，num 指定柱状图个数

>> X=normrnd(1,0.05,300,1);
>> subplot(2,1,1)
>> histfit(X)

>> subplot(2,1,2)
>> histfit(X,5)

Alex_McAvoy

Matlab 概率统计