Reference

多元变量函数，泰勒如何展开？（泰勒展开）

多元函数判断是否为函数值下降方向的直观理解

牛顿法与拟牛顿法学习笔记（一）牛顿法

机器学习笔记-牛顿法

机器学习笔记-牛顿法搜索方向的相关证明

【最优化】无约束优化方法-牛顿法

【最优化】无约束优化方法-阻尼牛顿法

梯度下降法、牛顿法和拟牛顿法

牛顿法与拟牛顿法

【概述】

牛顿法（Newton Method）又称牛顿迭代法，其是梯度下降法的进一步发展，是求解非线性优化问题的常用方法

梯度下降法利用目标函数的一阶偏导数信息，以负梯度方向作为搜索方向，仅考虑了目标函数在迭代点的局部性质，得到的仅是局部最优解（关于梯度下降法，详见：梯度下降法）

牛顿迭代法在梯度下降法的基础上，进一步利用了目标函数的二阶偏导数，这样就考虑了梯度变化的趋势，能够更加全面地确定合适的搜索方向以加快收敛，其具二阶收敛快速的特点

但牛顿迭代法对目标函数有着较为严格的要求，即函数必须具有连续的一、二阶偏导数，海森矩阵（Hessian Matrix）必须正定，此外，其每一步除了计算梯度外，还需要计算目标函数的海森矩阵与其逆矩阵，计算复杂、存储量大，以维数 $N$ 的平方比增加

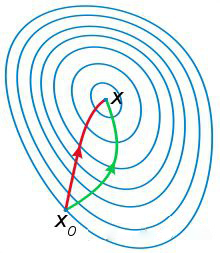
牛顿迭代法是二阶收敛，梯度下降法是一阶收敛，因此牛顿迭代法要比梯度下降法更快

如下图，红色路径代表牛顿迭代法，绿色路径代表梯度下降法

【牛顿迭代法的基本原理】

牛顿迭代法的原理，是使用函数 $f(x)$ 的泰勒级数，来寻找方程 $f(x)=0$ 根的个数

将 $f(x)$ 在 $x_0$ 处展开成泰勒级数，有：

$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+...$

取其线性部分的前两项，作为 $f(x)$ 的近似，即用 $f(x_0)+f’(x_0）(x-x_0)=0$ 的解来近似 $f(x)=0$ 的解

取 $x=x_1$，有：

$x_1=x_0-\frac{f(x_0)}{f'(x_0)}$

由于对 $f(x)$ 的近似只是一阶展开，因此 $x_1$ 并非 $f(x)=0$ 的解，只能说 $f(x_1)$ 比 $f(x_0)$ 更加接近于 $0$

因此，考虑迭代求解：

$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$

由于最开始是选用 $f(x_0)+f’(x_0)(x-x_0)=0$ 来进行近似，其本质是过点 $(x_0,f(x_0))$ 做曲线 $y=f(x)$ 的切线 $L:y=f(x_0)+f’(x_0)(x-x_0)$，近似解 $x_1=x_0-\frac{f(x_0)}{f’(x_0)}$ 为 $L$ 与 $x$ 轴交点的横坐标

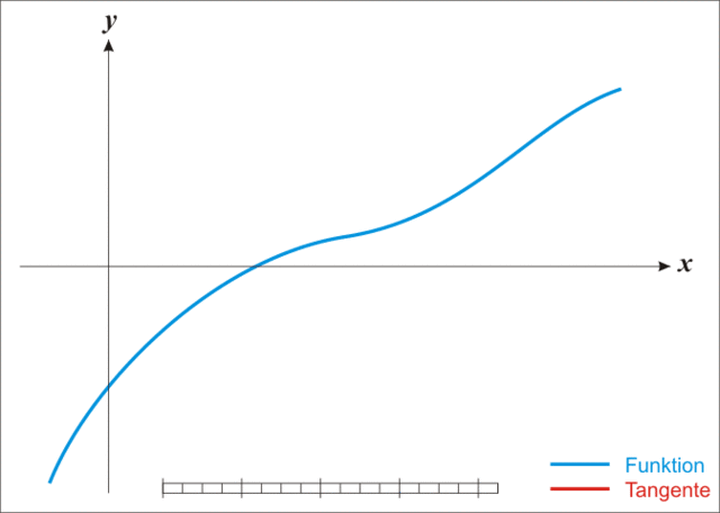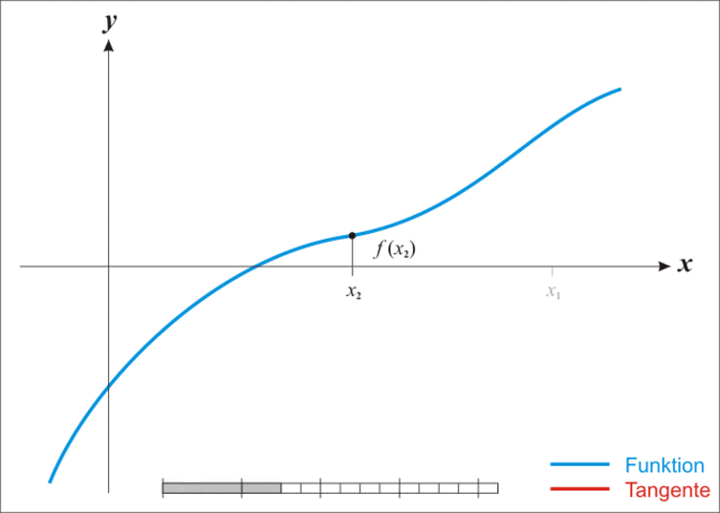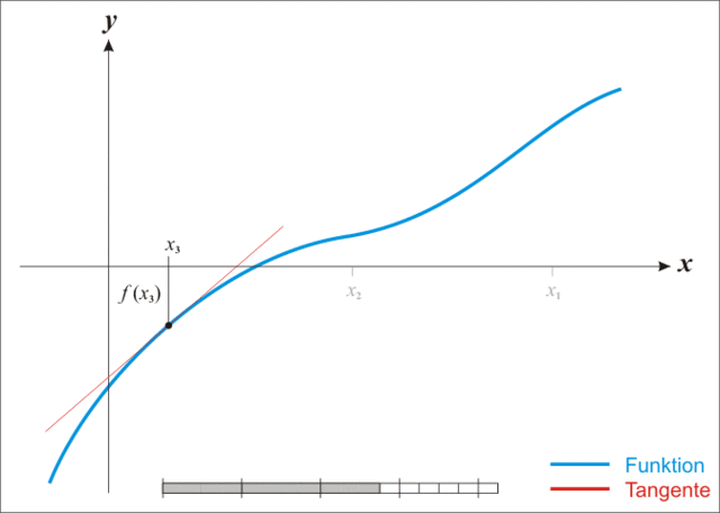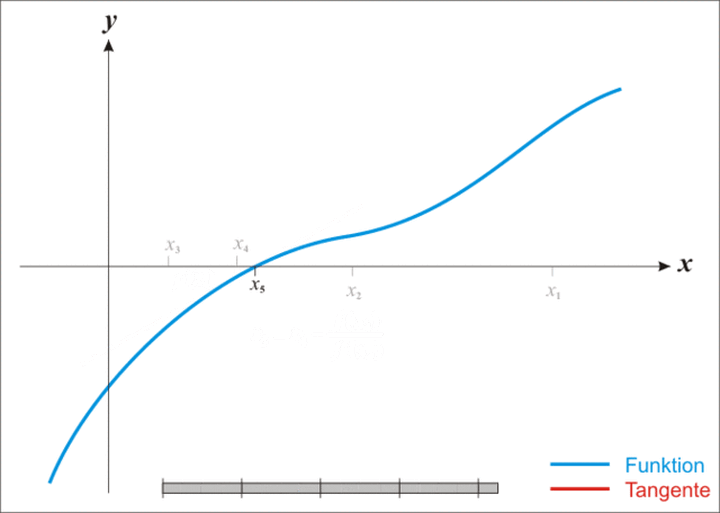
将上述过程进行推广，可以发现牛顿迭代法实质就是在曲线 $y=f(x)$ 上不断绘制点 $x_i$ 处的切线，来逼近 $f(x)$ 的解

迭代过程可参考下图

【海森矩阵与牛顿方向】

对于无约束极小化问题：

$\mathbf{x}^*=\arg \min_{\mathcal{X}} f(\mathbf{x})$

其中，$\mathbf{x}=(x^{(1)},x^{(2)},…,x^{(n)})^T\in \mathbb{R}^n$，$x^{(i)}$ 为向量 $\mathbf{x}$ 的第 $i$ 个分量

首先考虑 $n=1$ 的简单情形，此时 $\mathbf{x}=x$

设 $x_k$ 为当前的极小点估计值，使用牛顿迭代法进行求解，即在当前极小点估计值 $x_k$ 的附近对 $f(x)$ 做二阶泰勒展开，进而找到极小点的下一个估计值，有：

$\varphi(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{1}{2}f''(x_k)(x-x_k)^2+o^2(x)$

由于求的是最值，根据极值必要条件，$\varphi(x)$ 应满足：

$\varphi'(x)=0$

即：

$f'(x_k)(x-x_k)+\frac{1}{2}f''(x_k)(x-x_k)^2=0$

进而有：

$x=x_k-\frac{f'(x_k)}{f''(x_k)}$

于是，若给定初始值 $x_k$，则可构造如下的迭代格式：

$x_{k+1}=x_k-\frac{f'(x_k)}{f''(x_k)},\quad k=0,1,...$

产生序列 $\{x_k\}$ 来逼近 $f(x)$ 的极小点

对于 $n>1$ 的情景，设 $\mathbf{x_k}$ 为当前的极小点估计值，此时利用多元函数的二阶泰勒展开式，有：

$\varphi(\mathbf{x})=f(\mathbf{x_k})+\triangledown f(\mathbf{x_k})^T(\mathbf{x}-\mathbf{x_k})+\frac{1}{2}(\mathbf{x}-\mathbf{x_k})^T\triangledown^2 f(\mathbf{x_k})(\mathbf{x}-\mathbf{x_k})+o^2(\mathbf{x})$

其中，$\triangledown f$ 为 $f$ 的梯度向量，$\triangledown^2f$ 为 $f$ 的二阶偏导数构成的方阵，描述了函数的局部曲率，被称为海森矩阵（Hessian matrix）

$\triangledown f =\begin{bmatrix} \frac{\partial f}{\partial x^{(1)}} \\ \frac{\partial f}{\partial x^{(2)}} \\ \vdots \\ \frac{\partial f}{\partial x^{(n)}} \end{bmatrix},\quad \triangledown^2 f=\begin{bmatrix} \frac{\partial f^2}{\partial (x^{(1)})^2} &\frac{\partial f^2}{\partial x^{(1)}\partial x^{(2)}} &... & \frac{\partial f^2}{\partial x^{(1)} \partial x^{(n)}} \\ \frac{\partial f^2}{\partial x^{(2)} \partial x^{(1)}} &\frac{\partial f^2}{\partial (x^{(2)})^2} &... & \frac{\partial f^2}{\partial x^{(2)} \partial x^{(n)}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f^2}{\partial x^{(n)} \partial x^{(1)}} &\frac{\partial f^2}{\partial x^{(n)} \partial x^{(2)}} &... & \frac{\partial f^2}{\partial (x^{(n)})^2} \end{bmatrix}$

$\triangledown f$ 与 $\triangledown^2f$ 中的元素均为关于 $\mathbf{x}$ 的函数，将 $\triangledown f(\mathbf{x_k})$ 和 $\triangledown^2 f(\mathbf{x_k})$ 简记为 $\boldsymbol{g_k}$ 和 $H_k$，表示 $\mathbf{x}$ 取当前极小点估计值 $\mathbf{x_k}$ 后得到的梯度向量和海森矩阵

同样的，根据极值必要条件，$\varphi(\mathbf{x})$ 应满足：

$\triangledown \varphi(\mathbf{x})=0$

即：

$\boldsymbol{g_k}+H_k(\mathbf{x}-\mathbf{x_k})=0$

若海森矩阵 $H_k$ 为非奇异矩阵（矩阵可逆），则有：

$\mathbf{x}=\mathbf{x_k}-H_{k}^{-1}\cdot \boldsymbol{g_k}$

由此，若给定初值 $x_0$，则可构造如下的迭代格式：

$\mathbf{x_{k+1}}=\mathbf{x_k}-H_k^{-1}\cdot \boldsymbol{g_k},\quad k=0,1,...$

记：

$\boldsymbol{d_k}=-H_k^{-1}\cdot \boldsymbol{g_k}$

$\boldsymbol{d_k}$ 即为迭代过程中的迭代方向，被称为牛顿方向（Newton Direction），其是指向二次函数最优点的迭代方向，这个方向可正可负

【原始牛顿法】

原始牛顿迭代法即最原始的牛顿法（Newton Method），即在每次迭代时，迭代方向取牛顿方向 $\boldsymbol{d_k}$，每次迭代令 $\mathbf{x_{k+1}}=\mathbf{x_k}+\boldsymbol{d_k}$ 即可

下面给出原始牛顿法的完整算法描述：

给定初值 $\mathbf{x_0}$ 和精度阈值 $\varepsilon$，并令 $k=0$
计算凸函数 $f(\mathbf{x})$ 的梯度向量 $\boldsymbol{g_k}$ 和海森矩阵 $H_k$
若梯度向量的 L1 范数 $||\boldsymbol{g_k}||$ 满足 $||\boldsymbol{g_k}||<\varepsilon$，则停止迭代，否则执行步骤 4
根据牛顿方向 $\boldsymbol{d_k}=-H_k^{-1}\cdot \boldsymbol{g_k}$，计算新的迭代点 $\mathbf{x_{k+1}}=\mathbf{x_k}+\boldsymbol{d_k}$
令 $k=k+1$，转至步骤 2

如下图所示，实线是目标函数 $f(x)$，虚线是 $f(x)$ 在点 $x$ 处的二阶泰勒展开

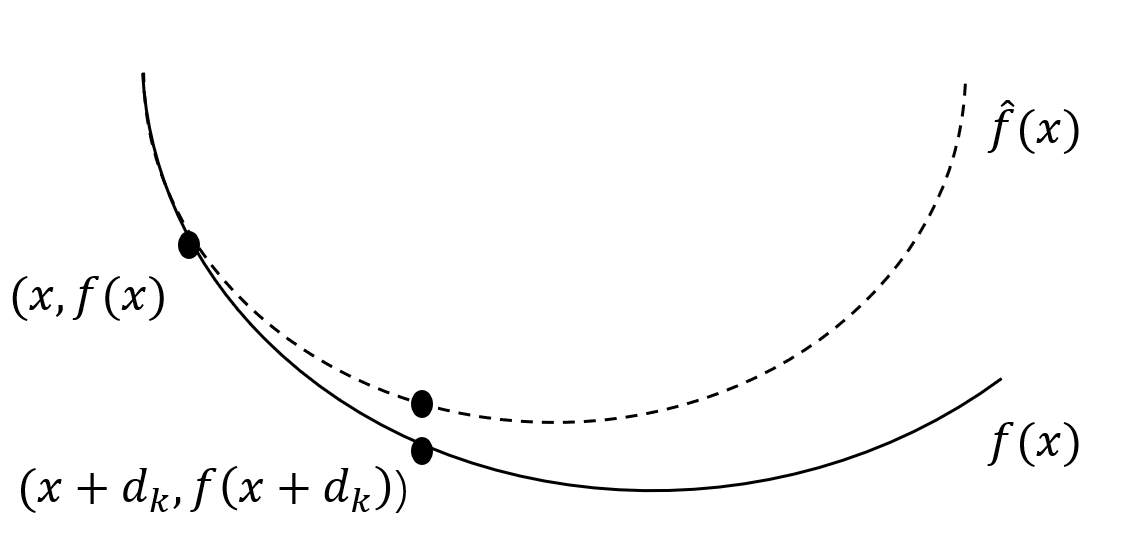
由于牛顿方向 $\boldsymbol{d_k}$ 可正可负，那么就需要知道在满足什么条件下牛顿法的迭代方向是下降的

首先给出下降方向（Descent Direction）的定义：

设 $f:\mathbb{R}^n\rightarrow \mathbb{R}^1$ 在点 $x$ 处可微，若存在 $\mathbf{p} \in \mathbb{R}^n$，使得：
$\triangledown f(x)^T \mathbf{p}<0$
则向量 $\mathbf{p}$ 是 $f$ 在 $x$ 处的下降方向

那么，在判断牛顿法的牛顿方向是否向函数值下降的方向移动时，就是判断迭代方向和当前点的梯度值做内积，即：

$\boldsymbol{d_k} \cdot \boldsymbol{g_k}^T = -H_k^{-1} \cdot \boldsymbol{g_k} \cdot \boldsymbol{g_k}^T$

若想让 $\boldsymbol{d_k} \cdot \boldsymbol{g_k}^T<0$，也就是令 $h_k^{-1} \cdot \boldsymbol{g_k} \boldsymbol{g_k}^t> 0$，即：

$H_k^{-1}>0$

可以发现，这恰好是海森矩阵正定的条件

也就是说，如果想要牛顿方向朝函数值下降的方向移动，就需要当前点的海森矩阵是正定的，而这个要求是极强的

因此，当目标函数是二次正定函数时，由于二阶泰勒展开函数与原目标函数不是近似，而是完全相同的二次式，此时海森矩阵 $H_k$ 退化为一个常数矩阵，从任意一初始点出发，利用迭代式 $\mathbf{x_{k+1}}=\mathbf{x_k}-H_k^{-1}\cdot \boldsymbol{g_k}$ 只需迭代一次即可达到 $f(x)$ 的极小值点 $x^*$

而当目标函数非二次函数，若函数的二次性态较强，或迭代点已进入到最优点的较小邻域，则其收敛速度同样很快；反之，则可能会出现函数值可能会上升的情况，即 $f(\mathbf{x_{k+1}})>f(\mathbf{x_k})$，在严重的情况下，甚至会导致迭代点列 $\{\mathbf{x_k}\}$ 的发散，以至于计算失败，这表明原始牛顿法不能保证迭代方向一定沿函数值下降方向

【阻尼牛顿法】

为解决原始牛顿法不能保证迭代方向一定沿函数值下降方向的问题，出现了阻尼牛顿法（Damped Newton’s Method）

在梯度下降法中，介绍了学习率 $\alpha$，即迭代步长，但在原始牛顿迭代法中，没有迭代步长这个概念，或者说在确定迭代方向后，迭代步长恒为 $1$

阻尼牛顿法是确定迭代方向后，继续在该方向进行一维搜索（Line Search），寻找在该迭代方向上最优的迭代步长 $\lambda$

阻尼牛顿法的牛顿方向与原始牛顿法一致，仍为 $\boldsymbol{d_k}=-H_k^{-1}\cdot \boldsymbol{g_k}$，寻找的迭代步长为：

$\lambda_k=\arg \min_{\lambda\in \mathbb{R}} f(\mathbf{x_k}+\lambda \boldsymbol{d_k})$

在引入步长因子 $\lambda_k$ 后，迭代式就变为：

$\mathbf{x_{k+1}}=\mathbf{x_k} - \lambda_k H_k^{-1}\cdot \boldsymbol{g_k},\quad k=0,1,...$

下面给出阻尼牛顿法的完整算法描述：

给定初值 $x_0$ 和精度阈值 $\varepsilon$，并令 $k=0$
计算凸函数 $f(\mathbf{x})$ 的梯度向量 $\boldsymbol{g_k}$ 和海森矩阵 $H_k$
若梯度向量的 L1 范数 $||\boldsymbol{g_k}||$ 满足 $||\boldsymbol{g_k}||<\varepsilon$，则停止迭代，否则确定搜索方向 $\boldsymbol{d_k}=-H_k^{-1}\cdot \boldsymbol{g_k}$
利用 $\lambda_k=\arg \min\limits_{\lambda\in \mathbb{R}} f(\mathbf{x_k}+\lambda \boldsymbol{d_k})$ 得到迭代步长 $\lambda_k$
令 $\mathbf{x_{k+1}}=\mathbf{x_k}- \lambda_k \boldsymbol{d_k}$
令 $k=k+1$，转至步骤 2

需要注意的是，无论是原始牛顿法还是阻尼牛顿法，均涉及到 $H_k^{-1}$ 的计算，在实际应用中，为追求效率，通常不直接对 $H_k$ 求逆，而是将其转换为求解线性方程组 $H_k \boldsymbol{d_k} = -\boldsymbol{g_k}$，此时可根据海森矩阵的性态来选择合适的迭代法，例如：预条件共轭梯度法（PCG）、代数多重网格法（AMG）等