Reference
【引入】
假设使用五把尺子,分别测量一个线段的长度,测量的结果如下:
| 尺子颜色 | 长度 |
|---|---|
| 红 | $10.2$ |
| 蓝 | $10.3$ |
| 橙 | $9.8$ |
| 黄 | $9.9$ |
| 绿 | $9.8$ |
使用不同的尺子测量,由于材质、精度等因素,会有误差出现,这种情况下,日常一般简单的取平均值作为线段的长度,即:
下面,换一种思路来思考这个问题
首先,将测量得到的值绘制在笛卡尔坐标系中,分别记作 $y_i$,同时将要猜测的线段长度的真实值用平行于横轴的虚线来表示,记作 $y$
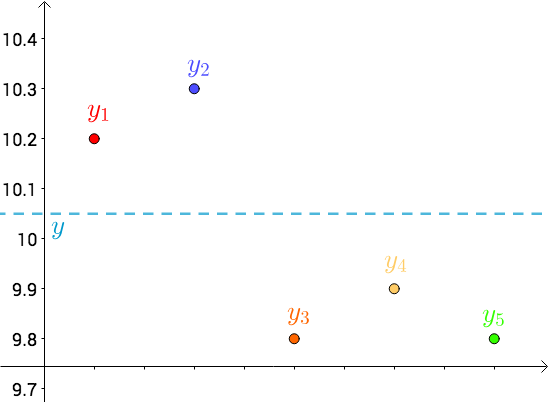
将每个点 $y_i$ 向猜测值 $y$ 作垂线,每个垂线的长度就是 $|y-y_i|$,可以理解为测量值与真实值的误差
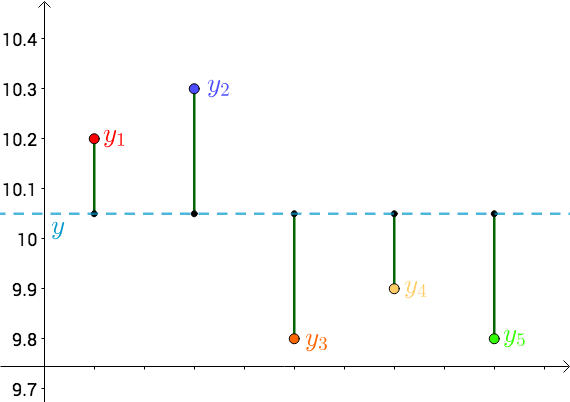
由于误差 $|y-y_i|$ 是长度,需要取绝对值,为后续计算方便,直接使用平方来代替误差,即:
那么,总的误差的平方即为残差平方和(Residual Sum of Squares,RSS):
关于 RSS 的详细介绍,见:回归问题的评价指标(二)
另一方面,由于猜测值 $y$ 是猜测的,其是不断变换的,那么,$RSS$ 也就不断在变换
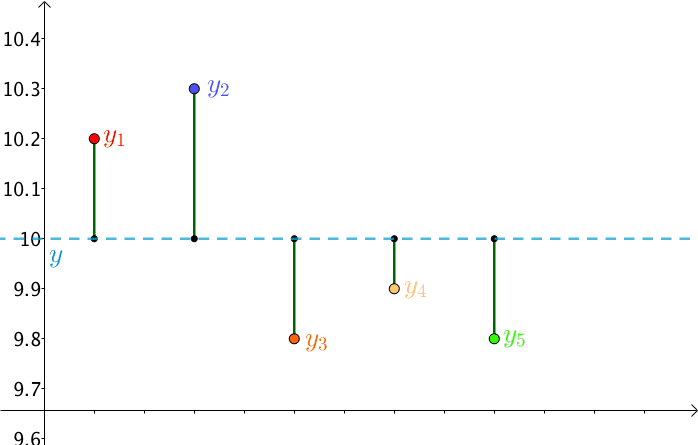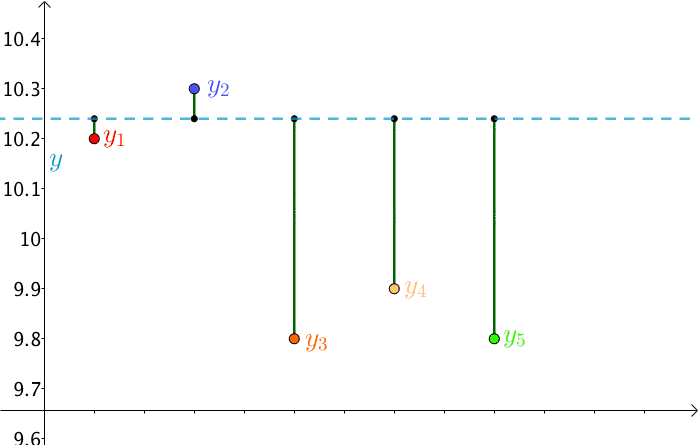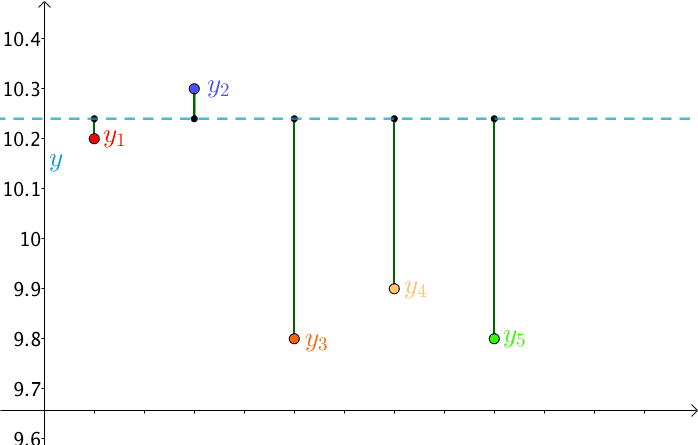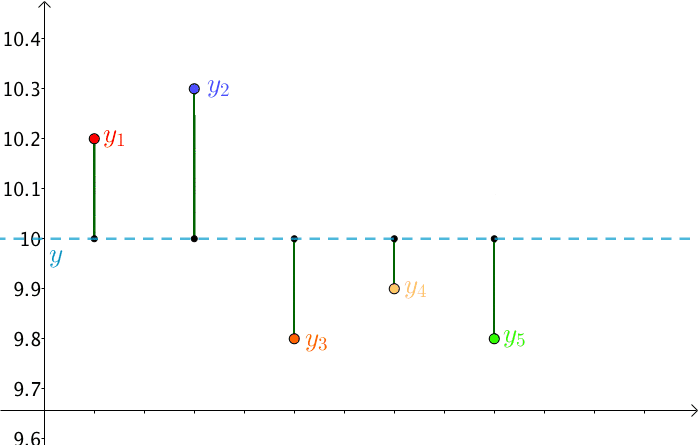
勒让德基于误差围绕真值上下波动,提出了最小二乘法(Least Sqaure Method),即让 $RSS$ 最小的 $y$ 就是真实值 $y^*$
【概述】
最小二乘法(Least Sqaure Method)是回归分析中的标准方法,该方法用于近似超定系统(Overdetermined System)答案,即一组包含未知数的方程组中,如果方程的数量大于未知数的数量,则系统就是一个超定系统,超定系统是无解的,只能求近似解,是一种解析解法
如下图,二维屏幕中有许多点,假设想用一条直线来拟合数据,即期望找到一条直线能最好地穿过这些数据点
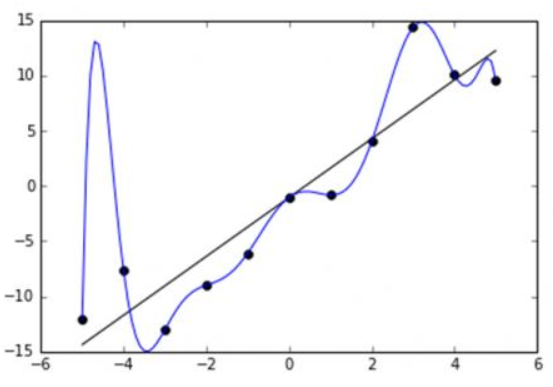
在图中,一个点即可构造一个方程,而显然有直线的斜率和截距两个未知数,因此这就是一个超定系统,是无法找到一条完美的直线,使得点均在直线上,因此,我们只能期望找到一条最好的适配直线(Best Fitting Line)来拟合这些数据
在机器学习中,目前应用的最广泛的普通最小二乘法(Ordinary Least Squares,OLS),常通过 OLS 来得到一个使目标函数最小化时的拟合函数的模型,一般形式为:
其中,观测值就是给定的多组样本,理论值就是假设的拟合函数,目标函数即损失函数
任务就是得到使目标函数最小化时的拟合函数
【普通最小二乘法】
假设形式
对于给定的容量为 $n$ 的样本集 $D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$,第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值,即:$\mathbf{x_i}=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})^T\in \mathbb{R}^m$,输出为 $y_i$
用假设函数 $f(\mathbf{x_i};\boldsymbol{\theta})$ 来表示对第 $i$ 组数据的预测结果:
其中,特征参数 $\boldsymbol{\theta}$ 为 $(m+1)\times 1$ 的列向量,即:
现在,希望求出相应的 $\{\theta^{(i)}\}^{m+1}_{i=0}$ 来使得 $f(\mathbf{x_i};\boldsymbol{\theta})$ 能够尽量地拟合样本集 $D$
为了表述方便,对假设函数进行简化,定义一个额外的第 $0$ 个特征量,这个特征量对所有样本的取值全部为 $1$,这使得特征量从过去的 $m$ 个变为 $m+1$ 个,即设:$x_i^{(0)}=1$
那么假设函数就可以写为:
将数据集 $D$ 写为 $(m+1)\times n$ 的矩阵,即:
同时,将样本中的 $y_i$ 也写为矩阵形式,即输出变量 $Y$ 为 $n\times 1$ 的列向量:
选用残差平方和 RSS 作为损失函数,则有:
最优化过程
要令目标函数最小,显然要令 $\frac{\partial}{\partial\boldsymbol{\theta}}J(\boldsymbol{\theta})=0$
对于 $\frac{\partial}{\partial\boldsymbol{\theta}}J(\boldsymbol{\theta})$,有:
关于详细证明,见:推导过程
之后,令 $\frac{\partial}{\partial\boldsymbol{\theta}}J(\boldsymbol{\theta})=0$,则有:
其中,$XX^T$ 为满秩矩阵,$(XX^T)^{-1}$ 为对应的逆矩阵
因此,只要根据样本给出的输入 $X$ 与输出 $Y$,若 $(XX^T)^{-1}$ 存在,即可计算出 $\boldsymbol{\theta}$ 的最优解:
推导过程
首先给出需要用到的矩阵求导公式:
对于 $n\times 1$ 的列向量 $\mathbf{x}$,与 $n\times 1$ 的列向量 $\mathbf{y}$,分母 $\mathbf{x}^T\mathbf{y}=\mathbf{y}^T\mathbf{x}$ 为标量,分子 $\mathbf{x}$ 为向量,求导为分母布局下的标量/向量的形式时,有:
对于 $n\times 1$ 的列向量 $\mathbf{x}$,与 $n\times n$ 的矩阵 $A$,分母 $\mathbf{x}^TA\mathbf{x}$ 为标量,分子 $\mathbf{x}$ 为向量,求导为分母布局下的标量/向量的形式时,有:
对于下列公式,进行推导:
式中,输入 $X$ 为 $(m+1)\times n$ 的矩阵,输出 $Y$ 为 $n\times 1$ 的列向量,特征参数 $\boldsymbol{\theta}$ 为 $(m+1)\times 1$ 的列向量
对于上式的第三项:
由于 $Y^TX^T\boldsymbol{\theta}$ 是一个标量,故有:
则:
因此,可得:
对于上式的第一项:
由于 $\boldsymbol{\theta}$ 为 $(m+1)\times 1$ 的列向量,$XX^T$ 为 $(m+1)\times (m+1)$ 的矩阵,故 $\theta^TXX^T\boldsymbol{\theta}$ 为标量,求导为分母布局下的标量/向量的形式,故有:
对于第二项:
$\boldsymbol{\theta}$ 为 $(m+1)\times 1$ 的列向量,$X^TY$ 为 $(m+1)\times 1$ 的矩阵,故 $\boldsymbol{\theta}^TXY$ 为标量,求导为分母布局下的标量/向量的形式,故有:
对于第三项:
显然有:
综上,可得:
【局限性与适用场景】
最小二乘法与梯度下降法、拟牛顿法这样的迭代法相比,似乎方便很多,但其仍有局限性
首先,最小二乘法需要计算 $XX^T$ 的逆矩阵 $(XX^T)^{-1}$,有可能这个逆矩阵不存在,这样就无法使用最小二乘法了,此时以梯度下降法为代表的迭代法仍可以使用。当然,可以通过对样本数据进行整理,去掉冗余特征,让 $XX^T$ 的行列式 $|XX^T|\neq 0$,然后继续采用最小二乘法
其次,当样本特征 $m$ 非常大时,$XX^T$ 是一个 $(m+1)\times(m+1)$ 的特征矩阵,对其求逆是一个十分耗时的工作,甚至不可行,此时以梯度下降法为代表的迭代法仍可以使用。一般来说,如果没有分布式大数据计算资源,超过 $10000$ 个特征就不建议使用最小二乘法了,如果一定要采用,可以使用 PCA 等降维的方法,降低特征维度后再使用最小二乘法
最后,如果拟合函数不是线性的,那么此时也无法使用最小二乘法,此时以梯度下降法为代表的迭代法仍可以使用。如果一定要采用最小二乘法,一般是利用线性微分方程来表示这个非线性的拟合函数,然后拟合线性微分方程的系数,再计算出对应的非线性函数的参数
下面给出梯度下降法与最小二乘法的对比:
| 梯度下降法 | 最小二乘法 | |
|---|---|---|
| 学习率 | 需要选择 | 不需要选择 |
| 计算方式 | 多次迭代 | 解析解法,一次运算得出 |
| 算法复杂度 | $O(km^2)$ | $O(m^3)$ |
| 适用情形 | 无论当特征数量 $m$ 多大均可 | 需计算矩阵的逆,特征数量 $m$ 较大时运算代价大 一般 $n<10000$ 时选用 |
| 适用算法 | 适用非线性、线性模型 | 只能用于线性模型 |

