向量范数与矩阵范数

【向量范数】

定义

在内积空间中，可以通过向量的内积来定义向量的长度 $|\alpha|=\sqrt{<\alpha,\alpha>}$，那么对于一般的线性空间，也可以引入一个类似长度的概念，即范数

设 $V$ 是数域 $F$ 上的线性空间，若 $\forall \alpha \in V$，都有一个实数 $||\alpha||$ 与之对应，且满足条件：

1. 正定性：$||\alpha||>0$ 且 $||\alpha||=0\Leftrightarrow \alpha=0$
2. 齐次性：$||k\alpha||=|k|\cdot||\alpha||,k\in F$
3. 三角不等式：$||\alpha+\beta||\leq ||\alpha||+||\beta||$

则称 $||\alpha||$ 为线性空间 $V$ 中向量的范数，定义了范数的线性空间称为线性赋范数空间，记为 $(V,||\cdot||)$

根据范数的定义可知，线性空间中范数的定义不是唯一的，在 $C^n$ 上可以找到无穷多种范数

等价性

设 $||\cdot||_{a}$ 和 $||\cdot||_b$ 是 $n$ 维线性空间 $V^n$ 中的任意两种范数，若存在常数 $M\geq m>0$，使得 $\forall \alpha\in V$，有

$$m||\alpha||_b\leq ||\alpha||_a\leq M||\alpha||_b$$

则称范数 $||\cdot||_a$ 与 $||\cdot||_b$ 等价，记为 $||\cdot||_a \sim ||\cdot||_b$

易知 $\sim$ 满足等价关系的三定律：

1. 自反律：$||\cdot||_a\sim||\cdot||_a$
2. 对称律：若 $||\cdot||_a\sim||\cdot||_b$，则 $||\cdot||_b\sim||\cdot||_a$
3. 传递律：若 $||\cdot||_a\sim||\cdot||_b,||\cdot||_a\sim||\cdot||_c$，则 $||\cdot||_a\sim||\cdot||_c$

常用范数

向量范数 $||\alpha||$ 可视为按照一定规律与向量 $\alpha$ 对应的非负实值函数，对 $\forall \mathbf{x}=[x_1,x_2,\cdots,x_n]^T\in C^n$，有

1）p 范数：常用于导出其他范数，当 $p$ 分别取 $0,1,2,\infty$ 时，有 0 范数、1 范数、2 范数、无穷范数

$$||\mathbf{x}||_p=\big({\sum_{i=1}^n|x_i|^p}\big)^{\frac{1}{p}}$$

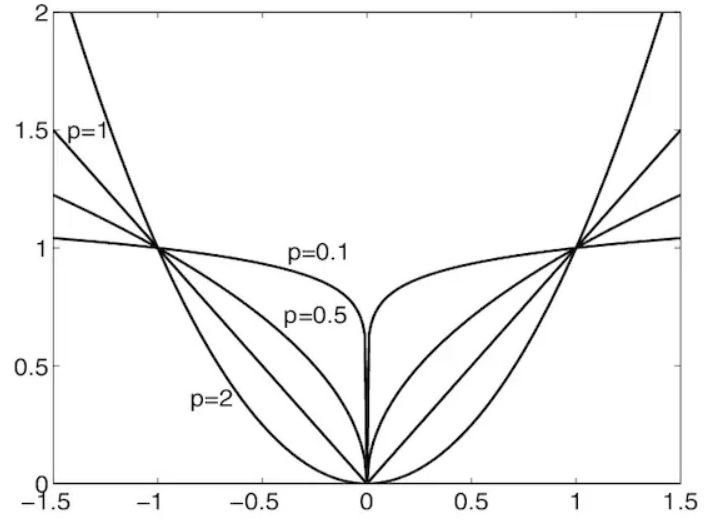
2）0 范数：向量 $\mathbf{x}$ 中非 $0$ 元素的个数，通常用于表示稀疏程度，$0$ 范数越小，表示 $0$ 元素就多，也就越稀疏

$$||\mathbf{x}||_0=\lim_{p\rightarrow0}\sum_{i=1}^n |x_i|^p=\#\{i:x_i\neq0\}$$

3）1 范数：表示向量 $\mathbf{x}$ 中所有元素的绝对值的和

$$||\mathbf{x}||_1=\sum_{i=1}^n|x_i|$$

4）2 范数：表示向量 $\mathbf{x}$ 中所有元素的均方根

$$||\mathbf{x}||_2=\sqrt{\sum_{i=1}^nx_i^2}$$

当线性空间 $V$ 为欧氏空间时，2 范数即为向量的长度 $||\mathbf{x}||=\sqrt{<\mathbf{x},\mathbf{x}>}$，被称为欧氏范数

5）无穷范数：表示向量 $\mathbf{x}$ 中各元素的绝对值的最大值

$$||\mathbf{x}||_\infty=\max{|x_i|}$$

【矩阵范数】

相容与协调

矩阵 $A$ 可视为 $C^{n}\rightarrow C^{m}$ 上的线性变换，那么矩阵范数 $||A||$ 与向量范数 $||\mathbf{x}||_{\alpha},||\mathbf{y}||_{\beta}$ 存在一定关系，为此给出如下定义

设 $||\cdot||_{\alpha}$，$||\cdot||_{\beta}$ 和 $||\cdot||_{\gamma}$ 是线性空间 $C^{m\times n}$、$C^{n\times p}$、$C^{m\times p}$ 中满足范数公理的矩阵范数，若 $\forall A\in C^{m\times n},B\in C^{n\times p}$ 有不等式

$$||AB||_{\gamma}\leq ||A||_{\alpha}\cdot||B||_{\beta}$$

成立，则称这三种矩阵范数 $||\cdot||_{\alpha}$，$||\cdot||_{\beta}$ 和 $||\cdot||_{\gamma}$ 是相容的

当 $p=1$ 时，有 $\forall \mathbf{x}\in C^n,A\mathbf{x}\in C^m$

$$||A\mathbf{x}||_{\gamma}\leq ||A||\cdot||\mathbf{x}||_{\beta}$$

此时称矩阵范数 $||\cdot||$ 和向量范数 $||\cdot||_{\beta},||\cdot||_{\gamma}$ 是协调的

等价性

与向量范数类似，对一般的矩阵范数，有如下性质：

1）设 $A=[a_{ij}]\in C^{m\times n}$，则 $A$ 的任一种矩阵范数 $||A||$ 都是 $A$ 的 $m\times n$ 个元素的连续函数

2）矩阵空间 $C^{m\times n}$ 上的任意两种矩阵范数 $||\cdot||_a,||\cdot||_b$ 都是等价的，即存在常数 $M\geq m\geq 0$，使得 $\forall A\in C^{m\times n}$ 有

$$m||A||_b\leq ||A||_a\leq M||A||_b$$

F 范数

设 $||\cdot||_{\alpha}$，$||\cdot||_{\beta}$ 和 $||\cdot||_{\gamma}$ 是线性空间 $C^{m\times n}$、$C^{n\times p}$、$C^{m\times p}$ 中满足范数公理的矩阵范数，当 $p=2$ 时，记由向量的 2 范数直接定义的矩阵范数为 $||A||_2$ 为

$$||A||_F=||A||_2=(\sum_{i=1}^m\sum_{j=1}^n|a_{ij}|^2)^{\frac{1}{2}}=\sqrt{tr(A^HA)}$$

称 $||A||_F$ 为 Frobenius 范数，简称 F 范数

其具有如下性质：

1）酉变换不影响 F 范数的值：设 $A\in C^{m\times n}$，对酉矩阵 $U\in C^{m\times m},V\in C^{n\times n}$，恒有

$$||A||_F=||UA||_F=||AV||_F=||UAV||_F$$

2）F 范数相容性：对 $\forall A\in C^{m\times n},B\in C^{n\times p}$，有

$$||AB||_F\leq ||A||_F\cdot ||B||_F$$

3）2 范数与 F 范数相容性：设 $A\in C^{m\times n}$，则 $||A||_F$ 与 $C^{m\times n},C^{n}$ 上的 2 范数 $||\cdot||_2$ 是相容的，即 $\forall \mathbf{x}\in C^{n}$ 有

$$||A\mathbf{x}||_2\leq ||A||_F\cdot ||\mathbf{x}||_2$$

诱导范数

与向量范数相容的最常用的矩阵范数是算子范数，其是利用向量范数是向量坐标的连续函数的性质诱导出来的，故也称为诱导范数

设 $A\in C^{m\times n}$，$\mathbf{x}=[x_1,x_2,\cdots,x_n]^T\in C^{n}$，$||\mathbf{x}||$ 和 $||A\mathbf{x}||$ 分别是 $C^{n}$ 和 $C^m$ 中的范数，则 $||A\mathbf{x}||$ 是 $(x_1,x_2,\cdots,x_n)$ 的连续函数，从而 $||A\mathbf{x}||$ 在有界闭集 $S=\{\mathbf{x}\in C^n|\:||\mathbf{x}||=1\}$ 上取极大值，则

$$||A||=\max_{||\mathbf{x}||=1}||A\mathbf{x}||=||A\mathbf{x}_0||,\quad x_0\in C^{n}$$

为一种相容的矩阵范数，其是由向量范数所诱导出来的一种矩阵范数，称为诱导范数

可以发现，求矩阵的诱导范数，相当于求函数 $||A\mathbf{x}||$ 在约束 $||\mathbf{x}||=1$ 下的条件极值

---

对于一般的向量范数而言，当向量范数分别取 1 范数、2 范数、无穷范数时，对应的矩阵的诱导范数分别称为矩阵的列范数、谱范数、行范数

设 $A=[a_{ij}]\in C^{m\times n}$，则

• 列范数：$||A||_1=\max\limits_{1\leq j\leq n} \sum\limits_{i=1}^m |a_{ij}|$
• 行范数：$||A||_{\infty}=\max\limits_{1\leq i\leq m} \sum\limits_{j=1}^n |a_{ij}|$
• 谱范数：$||A||_2=\sqrt{\max \lambda(A^HA)}$，其中 $\lambda(A^HA)$ 代表 $A^HA$ 的特征值

谱半径

设 $A\in C^{n\times n}$，称

$$S_p(A)=\{\lambda|\lambda 为 A 的特征值\}$$

为 $A$ 的谱，称

$$\rho(A)=\max|S_p(A)|$$

为 $A$ 的谱半径

按照定义，有

$$||A||_2=\sqrt{\rho(A^HA)}$$

特别地，当 $A$ 是 Hermite 矩阵时，有

$$||A||_2=\rho(A)$$

当 $A\in C^{n\times n}$，$||A||$ 是 $A$ 的任意一种诱导范数时，有

$$\rho(A)\leq ||A||$$