信息增益与信息增益比

【信息增益与互信息】

在决策树中，信息增益（Information Gain）表示在知道了特征 $X$ 的信息后，使得使类 $Y$ 的信息的不确定性减少了的程度

信息增益是针对特征而言的，因此，特征 $A$ 对于训练集 $D$ 的信息增益 $g(D,A)$，被定义为：训练集 $D$ 的经验信息熵 $H(D)$ 与给定条件下特征 $A$ 与训练集 $D$ 的经验条件熵 $H(D|A)$ 的差，即：

$$g(D,A)=H(D)-H(D|A)$$

而对于二维离散型随机变量 $(X,Y)$ 来说，信息熵 $H(X)$ 与条件熵 $H(X|Y)$ 的差被定义为互信息 $I(X,Y)$，也就是说，在决策树中，信息增益就是训练数据集中类与特征的互信息

对于训练集 $D$ 而言，其每个特征都有一个信息增益值，在出现训练集经验信息熵大（分类困难）时，信息增益值会偏大，反之信息增益值会偏小，而信息增益值大的特征，具有更强的分类能力

【信息增益算法】

对于样本容量为 $|D|$ 的训练集 $D$，设其有 $K$ 个类 $C_k,k=1,2,…,K$，每个类中的样本个数为 $|C_k|$，则有：

$$\sum_{k=1}^K|C_k|=|D|$$

设特征 $A$ 有 $n$ 个不同的取值 $\{a_1,a_2,…,a_n\}$，根据特征 $A$ 的取值将 $D$ 划分为 $n$ 个子集 $D_1,D_2,…,D_n$，并用 $|D_i|$ 表示划分子集 $D_i$ 中的样本数，同样有：

$$\sum_{i=1}^n|D_i|=|D|$$

记子集 $D_i$ 中属于类 $C_k$ 的样本的集合为 $D_{ik}$，其样本数为 $|D_{ik}|$，即：

$$D_{ik}=D_i\cap C_k$$

---

下面给出计算信息增益的算法：

输入：训练集 $D$ 与特征 $A$

输出：特征 $A$ 对于训练集 $D$ 的信息增益 $g(D,A)$

1.计算训练集 $D$ 的经验信息熵

$$\begin{align*} H(D) &= -\sum_{k=1}^Kp_k\log p_k \\ &= -\sum_{k=1}^K\frac{|C_k|}{|D|}\log\frac{|C_k|}{|D|} \end{align*}$$

2.计算特征 $A$ 对训练集 $D$ 的经验条件熵 $H(D|A)$

$$\begin{align*} H(D|A) &= -\sum_{i=1}^np(a_i)H(D|A=a_i)\\ &= -\sum_{i=1}^n p(a_i) \sum_{k=1}^K p(C_k|a_i)\log p(C_k|a_i) \\ &= -\sum_{i=1}^n \frac{|D_i|}{|D|} \sum_{k=1}^K \frac{|D_{ik}|}{|D_i|}\log(\frac{|D_{ik}|}{|D_i|}) \\ \end{align*}$$

3.计算信息增益 $g(D,A)$

$$g(D,A) = H(D)-H(D|A)$$

【信息增益比】

当以信息增益作为划分训练集的特征时，存在偏向于选择取值较多的特征的问题，使用信息增益比（Information Gain Radio）可以对这个问题进行校正，使得偏向于选择取值较少的特征，这是特征选择的另一个标准

对于训练集 $D$ 关于特征 $A$ 的信息熵 $H_A(D)$，有：

$$\begin{align*} H_A(D) &= -\sum_{x}p(x)\log p(x) \\ &=-\sum_{i=1}^n\frac{|D_i|}{|D|}\log\frac{|D_i|}{|D|} \end{align*}$$

其中，$|D|$ 是训练集的样本个数，$|D_i|$ 是特征 $A$ 上第 $i$ 个取值的个数，$n$ 是特征 $A$ 的取值个数

简单来说，$H_A(D)$ 是将特征 $A$ 作为一个随机变量，其取值是 $A$ 的各个特征值，而求得的信息熵

对于特征 $A$ 与训练集 $D$ 的信息增益比 $g_R(D,A)$，其被定义为信息增益 $g(D,A)$ 与训练集 $D$ 关于特征 $A$ 的信息熵 $H_A(D)$ 的比，即：

$$g_R(D,A) = \frac{g(D,A)}{H_A(D)}$$

可以发现，信息增益比的本质，是在信息增益的基础上乘以一个惩罚参数 $\frac{1}{H_A(D)}$，当特征 $A$ 取值数量 $n$ 较大时，惩罚参数较小；当特征 $A$ 取值数量 $n$ 较小时，惩罚参数较大

基于上述问题，在使用信息增益比时，并不是直接选择信息增益率最大的特征，而是使用一种启发式方法：

1. 在候选特征中找出信息增益高于平均水平的特征
2. 在这些高于平均水平的特征中再选择信息增益率最高的特征作为特征选择的标准

【实例】

信息增益

以下表为例，计算信息增益

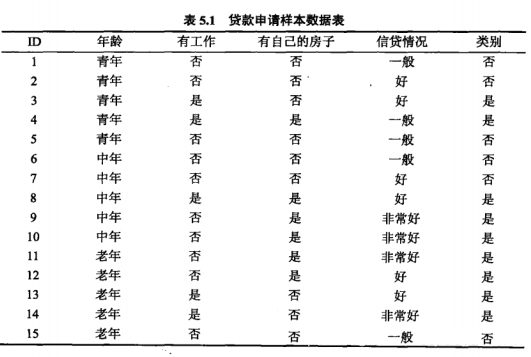
在上表中，有 $|D|=15$ 个数据，存在 $A=4$ 个特征，分别用 $A_1$、$A_2$、$A_3$、$A_4$ 来表示年龄、有无工作、有无房子、信贷情况，最终分类结果只有两类，即放贷、不放贷，有：$K=2$

根据统计，9 个数据结果为放贷，6 个数据结果为不放贷，记放贷为 $C_1$ 类，不放贷为 $C_2$ 类

1.计算信息经验熵：

$$\begin{align*} H(D) &= -\sum_{k=1}^K\frac{|C_k|}{|D|}\log\frac{|C_k|}{|D|} \\ &= -(\frac{|C_1|}{|D|}\log\frac{|C_1|}{|D|}+\frac{|C_2|}{|D|}\log \frac{|C_2|}{|D|}) \\ &= -(\frac{|9|}{|15|}\log\frac{|9|}{|15|}+\frac{|6|}{|15|}\log \frac{|6|}{|15|}) \\ &= 0.971 \end{align*}$$

2.计算各特征的经验条件熵：

对于年龄 $A_1$，其有三个取值：青年、中年、老年，划分子集后有 $|D_1|=5$，$|D_2|=5$，$|D_3|=5$，这三个子集属于放贷类 $C_1$ 的样本集合分别有 $|D_{11}|=2$，$|D_{21}|=3$，$|D_{31}|=4$ 个样本，属于不放贷类 $C_2$ 的样本集合分别有 $|D_{12}|=3$，$|D_{22}|=2$，$|D_{32}|=1$ 个样本，则：

$$\begin{align*} H(D|A_1) &= -\sum_{i=1}^n \frac{|D_i|}{|D|} \sum_{k=1}^K \frac{|D_{ik}|}{|D_i|}\log(\frac{|D_{ik}|}{|D_i|}) \\ &= -\bigl[\frac{5}{15}(\frac{2}{5}\log\frac{2}{5}+\frac{3}{5}\log\frac{3}{5})+\frac{5}{15}(\frac{3}{5}\log\frac{3}{5}+\frac{2}{5}\log\frac{2}{5}) \\ & \quad+ \frac{5}{15}(\frac{4}{5}\log\frac{4}{5}+\frac{1}{5}\log\frac{1}{5})\bigr] \\ &= 0.888 \end{align*}$$

对于有无工作 $A_2$，其有两个取值：有、无，划分子集后有 $|D_1|=5$，$|D_2|=10$，这两个子集属于放贷类 $C_1$ 的样本集合分别有 $|D_{11}|=5$，$|D_{21}|=0$ 个样本，属于不放贷类 $C_2$ 的样本集合分别有 $|D_{12}|=4$，$|D_{22}|=6$ 个样本，则：

$$\begin{align*} H(D|A_2) &= -\sum_{i=1}^n \frac{|D_i|}{|D|} \sum_{k=1}^K \frac{|D_{ik}|}{|D_i|}\log(\frac{|D_{ik}|}{|D_i|}) \\ &= -\bigl[\frac{5}{15}(\frac{5}{5}\log\frac{5}{5}+\frac{0}{5}\log\frac{0}{5})+\frac{10}{15}(\frac{4}{10}\log\frac{4}{10}+\frac{6}{10}\log\frac{6}{10}) \\ &= 0.647 \end{align*}$$

对于有无房子 $A_3$，其有两个取值：有、无，划分子集后有 $|D_1|=6$，$|D_2|=9$，这两个子集属于放贷类 $C_1$ 的样本集合分别有 $|D_{11}|=6$，$|D_{21}|=0$ 个样本，属于不放贷类 $C_2$ 的样本集合分别有 $|D_{12}|=3$，$|D_{22}|=6$ 个样本，则：

$$\begin{align*} H(D|A_3) &= -\sum_{i=1}^n \frac{|D_i|}{|D|} \sum_{k=1}^K \frac{|D_{ik}|}{|D_i|}\log(\frac{|D_{ik}|}{|D_i|}) \\ &= -\bigl[\frac{6}{15}(\frac{6}{6}\log\frac{6}{6}+\frac{0}{6}\log\frac{0}{6}) + \frac{9}{15}(\frac{3}{9}\log\frac{3}{9}+\frac{6}{9}\log\frac{6}{9}) \\ &= 0.551 \end{align*}$$

对于信贷情况 $A_4$，其有三个取值：一般、好、非常好，划分子集后有 $|D_1|=5$，$|D_2|=6$，$|D_3|=4$，这三个子集属于放贷类 $C_1$ 的样本集合分别有 $|D_{11}|=1$，$|D_{21}|=4$，$|D_{31}|=4$ 个样本，属于不放贷类 $C_2$ 的样本集合分别有 $|D_{12}|=4$，$|D_{22}|=2$，$|D_{32}|=0$ 个样本，则：

$$\begin{align*} H(D|A_4) &= -\sum_{i=1}^n \frac{|D_i|}{|D|} \sum_{k=1}^K \frac{|D_{ik}|}{|D_i|}\log(\frac{|D_{ik}|}{|D_i|}) \\ &= -\bigl[\frac{5}{15}(\frac{1}{5}\log\frac{1}{5}+\frac{4}{5}\log\frac{4}{5}) + \frac{6}{15}(\frac{4}{6}\log\frac{4}{6}+\frac{2}{6}\log\frac{2}{6}) \\ & \quad+ \frac{4}{15}(\frac{4}{4}\log\frac{4}{4}+\frac{0}{4}\log\frac{0}{4})\bigr] \\ &= 0.608 \end{align*}$$

3.计算各特征的信息增益

$$\begin{matrix} g(D,A_1)=H(D)-H(D|A_1) = 0.083\\ g(D,A_2)=H(D)-H(D|A_2) = 0.324\\ g(D,A_3)=H(D)-H(D|A_3) = 0.420\\ g(D,A_4)=H(D)-H(D|A_4) = 0.363 \end{matrix}$$

此时，选择信息增益最大的 $A_3$ 作为最优特征

信息增益比

以上例的信息增益为基础，继续计算信息增益比

1.计算平均信息增益，选择高于平均水平的信息增益

$$\begin{align*} \bar{g}(D,A) &= \frac{1}{n}\sum\limits_{i=1}^ng(D,A_i) \\ &= \frac{1}{4}\cdot 1.19 \\ &= 0.298 \end{align*}$$

此时，高于 $\bar{g}(D,A)$ 的有：

$$\begin{matrix} g(D,A_2)= 0.324\\ g(D,A_3)= 0.420\\ g(D,A_4)= 0.363 \end{matrix}$$

2.计算训练集关于各特征的信息熵

对于特征 $A_2$，其有两个取值：有、无，划分子集后有 $|D_1|=5$，$|D_2|=10$，此时：

$$\begin{align*} H_{A_2}(D) &= -\sum_{i=1}^n\frac{|D_i|}{|D|}\log\frac{|D_i|}{|D|} \\ &=-( \frac{5}{15}\log\frac{5}{15}+\frac{10}{15}\log\frac{10}{15}) \\ &= 0.918 \end{align*}$$

对于特征 $A_3$，其有两个取值：有、无，划分子集后有 $|D_1|=6$，$|D_2|=9$，此时：

$$\begin{align*} H_{A_3}(D) &= -\sum_{i=1}^n\frac{|D_i|}{|D|}\log\frac{|D_i|}{|D|} \\ &= -(\frac{6}{15}\log\frac{6}{15}+\frac{9}{15}\log\frac{9}{15}) \\ &= 0.971 \end{align*}$$

对于特征 $A_4$，其有三个取值：一般、好、非常好，划分子集后有 $|D_1|=5$，$|D_2|=6$，$|D_3|=4$，此时：

$$\begin{align*} H_{A_4}(D) &= -\sum_{i=1}^n\frac{|D_i|}{|D|}\log\frac{|D_i|}{|D|} \\ &= -(\frac{5}{15}\log\frac{5}{15}+\frac{6}{15}\log\frac{6}{15}+\frac{4}{15}\log\frac{4}{15}) \\ &= 1.566 \end{align*}$$

3.计算各特征的信息增益比

$$\begin{matrix} g_R(D,A_2)=\frac{g(D,A_2)}{H_{A_2}(D)}= 0.353 \\ g_R(D,A_3)=\frac{g(D,A_3)}{H_{A_3}(D)}= 0.433 \\ g_R(D,A_4)=\frac{g(D,A_4)}{H_{A_4}(D)}= 0.232 \\ \end{matrix}$$

此时，选择信息增益比最大的 $A_3$ 作为最优特征