基尼指数

【概率分布的基尼指数】

基尼指数表示在样本集合中一个随机选中的样本被分错的概率，与信息熵相似，基尼指数越大，样本集合 $D$ 的不确定性也就越大

假设有 $K$ 个类，样本点属于第 $k$ 类的概率为 $p_k$，则概率分布的基尼指数定义为：

$$\begin{align*} Gini(p) &=\sum_{k=1}^Kp_k(1-p_k) \\ &= 1-\sum_{k=1}^Kp_k^2 \end{align*}$$

如下图，显示了在二分类问题中，基尼指数 $Gini(p)$、半信息熵 $\frac{1}{2}H(p)$ 与分类误差率的关系，其中横坐标为概率 $p$，纵坐标为损失

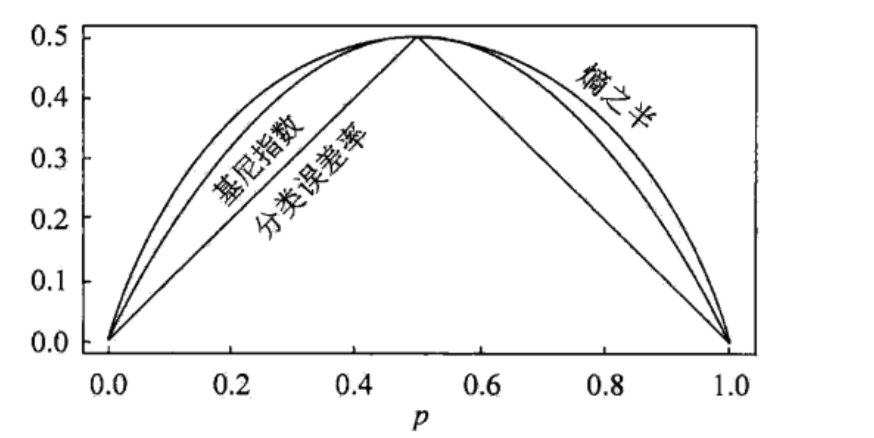
可以看出，基尼指数与半信息熵的曲线十分接近，均可来近似的表示分类误差率

根据泰勒公式，$\ln(x)=-1+x+o(x)$，因此：

$$\begin{align*} H(X) &=-\sum_{k=1}^Kp_k\ln p_k\\ &\approx \sum_{k=1}^Kp_k(1-p_k) \end{align*}$$

也就是说，基尼指数，可以理解为信息熵的一阶泰勒展开

【二分类的基尼指数】

对于二分类问题来说，若样本点属于第一个类的概率为 $p$，则其属于第二个类的概率为 $1-p$，相应地，基尼指数为：

$$\begin{align*} Gini(p) &= 1-\sum_{k=1}^Kp_k^2 \\ &= 1-p^2-(1-p)^2 \\ &= 1-p^2-1+2p-p^2 \\ &= 2p-2p^2 \\ &= 2p(1-p) \end{align*}$$

【多分类的基尼指数】

对于给定的样本集合 $D$，其样本数为 $|D|$，分为 $K$ 类，属于第 $k$ 类的样本子集 $C_k$ 的样本数为 $|C_k|$，则基尼指数为：

$$Gini(D)=1-\sum_{k=1}^K\bigl(\frac{|C_k|}{|D|}\bigr)^2$$

若样本集合 $D$ 根据特征 $A$ 可能取值 $a_i$，被分割为 $D_1,D_2,…,D_m$ 的 $m$ 个部分，记 $D_i$ 中属于类 $C_k$ 的样本集合为 $D_{ik}$，其样本数为 $|D_{ik}|$，则在特征 $A$ 的条件下，集合 $D$ 的基尼指数为：

$$\begin{align*} Gini(D,A) &=\sum_{i=1}^m\frac{|D_i|}{|D|}Gini(D_i) \\ &= \sum_{i=1}^m\frac{|D_i|}{|D|}\bigl[1-\sum_{k=1}^K\bigl(\frac{|D_{ik}|}{|D_i|}\bigr)^2\bigr]\\ \end{align*}$$

特别地，对于二分类问题，在特征 $A$ 的条件下，集合 $D$ 的基尼指数定义为：

$$Gini(D,A)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$$

基尼指数 $Gini(D)$ 表示样本集合 $D$ 的不确定性，而基尼指数 $Gini(D,A)$ 表示了经过 $A=a_i$ 分割后集合 $D$ 的不确定性