【概述】
Word2Vec 模型,是由谷歌提出的一套新的词嵌入(Word Embedding)方法,其实质上是一个简单的神经网络
该模型能够学习一个从高维稀疏离散向量到低维稠密连续向量的映射,该映射具有近义词向量的欧氏距离小,词向量之间的加减法有实际物理意义等特点
其输入层、隐藏层、输出层均仅一层,根据输入输出的不同,具有两种训练模式:
- CBOW 模型:根据上下文单词预测目标词
- Skip-Gram 模型:根据目标词预测上下文单词
一般神经网络语言模型在预测的时候,输出的是预测目标词的概率,也就是说每一次预测都要基于全部的数据集进行计算,这无疑会带来很大的时间开销,为此,Word2Vec 提出两种加快训练速度的方式,一种是层次 Softmax(Hierarchical Softmax),另一种是 负采样(Negative Sampling),这里不再进行介绍
【CBOW 模型】
连续词袋模型(Continuous Bag of Words,CBOW)通过给定的上下文单词来预测目标词,相当于在一句话中扣掉一个词,然后猜这个词是什么

其网络结构如下图
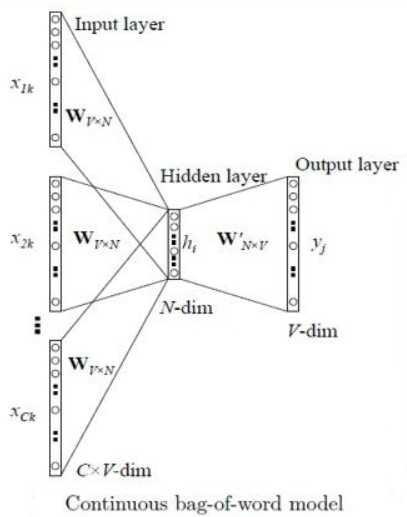
符号说明:
| 符号 | 说明 |
|---|---|
| $C$ | 上下文单词个数 |
| $V$ | 单词向量空间维度 (One-Hot 编码向量长度) |
| $N$ | 词向量维度,大小任意 |
| $\mathbf{x}_1,\mathbf{x}_2,\cdots, \mathbf{x}_{C}\in\mathbb{R}^{V\times 1}$ | 输入层向量 (One-Hot 编码向量) |
| $\mathbf{h}\in \mathbb{R}^{N\times 1}$ | 隐藏层向量 |
| $\mathbf{y}\in\mathbb{R}^{V\times 1}$ | 输出层向量 (每一维代表所对应的单词作为预测词的概率) |
| $\mathbf{v}_1,\mathbf{v}_2,\cdots,\mathbf{v}_C\in\mathbb{R}^{N\times 1}$ | 词向量 |
| $W\in \mathbb{R}^{V\times N}$ | 输入权重矩阵 (目标词向量矩阵) |
| $W’\in \mathbb{R}^{N\times V}$ | 输出权重矩阵 (上下文向量矩阵) |
具体流程如下:
Step1:输入 $C$ 个上下文单词的 One-Hot 编码向量 $\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_{C}$
Step2:将所有的 One-Hot 编码向量 $\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_{C}$ 分别与输入权重矩阵 $W$ 相乘,得到大小为 $N\times 1$ 的词向量 $\mathbf{v}_1,\mathbf{v}_2,\cdots,\mathbf{v}_C$
Step3:将所得的 $C$ 个大小为 $N\times 1$ 词向量 $\mathbf{v}_1,\mathbf{v}_2,\cdots,\mathbf{v}_C$ 相加求平均作为隐藏层向量 $\mathbf{h}$
Step4:将隐藏层向量 $\mathbf{h}$ 与输出层权重矩阵 $W’$ 相乘,得到大小为 $V\times 1$ 的向量 $\mathbf{u}$
Step5:将向量 $\mathbf{u}$ 利用 softmax 函数处理,得到最终的输出 $\mathbf{y}$,每一维代表所对应的单词作为预测词的概率
综上所述,需要定义一个损失函数来更新两个权重矩阵 $W$ 和 $W’$,一般采用交叉熵损失函数和梯度下降法来训练
【Skip-Gram 模型】
Skip-Gram 模型通过给定的目标词来预测上下文单词,相当于给定一个词,然后猜前面和后面可能出现什么词

其网络结构如下图
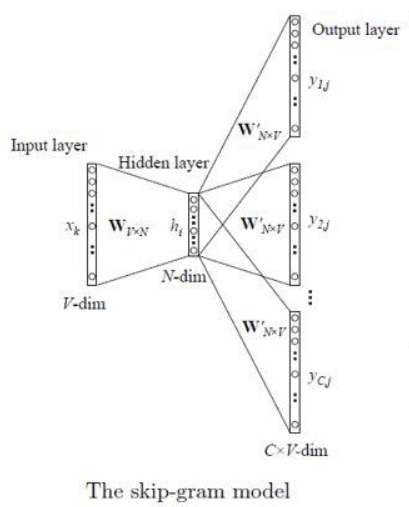
符号说明:
| 符号 | 说明 |
|---|---|
| $V$ | 单词向量空间维度 (One-Hot 编码向量长度) |
| $N$ | 词向量维度,大小任意 |
| $\mathbf{x}\in\mathbb{R}^{V\times 1}$ | 输入层向量 (One-Hot 编码向量) |
| $\mathbf{h}\in \mathbb{R}^{N\times 1}$ | 隐藏层向量 |
| $\mathbf{y}_1,\mathbf{y}_2,\cdots,\mathbf{y}_C\in \mathbb{R}^{V\times 1}$ | 输出层向量 (每一维代表所对应的单词作为预测词的概率) |
| $\mathbf{v}\in \mathbb{R}^{N\times 1}$ | 词向量 |
| $W\in \mathbb{R}^{V\times N}$ | 输入权重矩阵 (目标词向量矩阵) |
| $W’\in \mathbb{R}^{N\times V}$ | 输出权重矩阵 (上下文向量矩阵) |
具体流程如下:
Step1:输入 $1$ 个目标词的 One-Hot 编码向量 $\mathbf{x}$
Step2:将的 One-Hot 编码向量 $\mathbf{x}$ 与输入权重矩阵 $W$ 相乘,得到大小为 $N\times 1$ 的隐藏层向量 $\mathbf{h}$
Step3:将所得的隐藏层向量 $\mathbf{h}$ 与输出层权重矩阵 $W’$ 相乘,得到大小为 $V\times 1$ 的向量 $\mathbf{u}$,每一维度代表目标词与其他词的相似度
Step4:将向量 $\mathbf{u}$ 利用 softmax 函数处理,得到最终的输出 $\mathbf{y}$,每一维代表所对应的单词作为预测词的概率
综上所述,需要定义一个损失函数来更新两个权重矩阵 $W$ 和 $W’$,一般采用交叉熵损失函数和梯度下降法来训练

