【概述】

具有噪声的基于密度的聚类方法（Density-Based Spatial Clustering of Applications with Noise，DBSCAN）是一种基于密度的空间聚类算法，该算法将簇定义为密度相连的点的最大集合，能够将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇

DBSCAN 不要求指定簇的数量，避免了异常值，并且没有质心，聚类簇是通过将相邻的点连接在一起的过程形成的

【基本概念】

DBSCAN 通过一组邻域（Neighborhood）参数 $(\epsilon,\text{MinPts})$ 来刻画样本分布的紧密程度

对于给定的样本集 $D=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\}$，有如下基本概念：

1）最大半径 $\epsilon$：，用来确定两个点是否相似和属于同一类的距离，更大的 $\epsilon$ 包含更多的数据点，从而产生更大的簇，反之，更小的 $\epsilon$ 将构建更小的簇

对 $\mathbf{x}_i\in D$，其 $\epsilon$-邻域包含样本集 $D$ 中与 $\mathbf{x}_i$ 的距离不大于 $\epsilon$ 的样本，即

$N_{\epsilon}(\mathbf{x}_i) = \{\mathbf{x}\in D| \text{dist}(\mathbf{x}_i,\mathbf{x}_j)\leq \epsilon \}$

2）最小点 $\text{MinPts}$：在一个邻域的最大半径内，$\text{MinPts}$ 个及以上的点被视为一个簇

例如 $\text{MinPts}=4$，则在该邻域的最大半径内，$4$ 个及以上的点被认为是一个簇

3）核心点（Core Point）：若 $\mathbf{x}_i$ 的 $\epsilon$-邻域中至少包含 $\text{MinPts}$ 个样本，则 $\mathbf{x}_i$ 是一个核心点，即

$|N_{\epsilon}(\mathbf{x}_i)| \geq \text{MinPts}$

4）近邻点（Neighbor Point）：若 $\mathbf{x}_i$ 是一个核心点，那么位于其 $\epsilon$-邻域边界内的样本点，是近邻点

5）边界点（Border Point）：若 $\mathbf{x}_i$ 是一个核心点，那么位于其 $\epsilon$-邻域边界上的样本点，是边界点

6）离群点（Outlier）：若 $\mathbf{x}_i$ 是一个核心点，那么其非近邻点、非边界点，是离群点

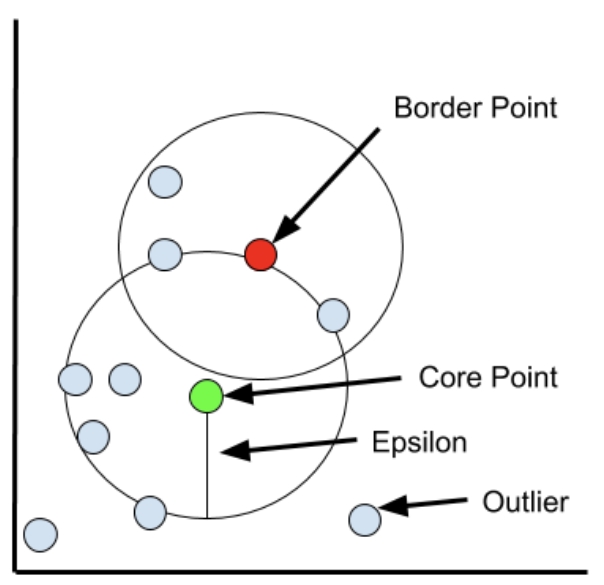
如下图所示，展示了最大半径 $\epsilon$、核心点、边界点、离群点

7）密度直达（Directly Density-reachable）：若 $\mathbf{x}_j$ 位于核心点 $\mathbf{x}_i$ 的 $\epsilon$ 邻域内，则称 $\mathbf{x}_j$ 由 $\mathbf{x}_i$ 密度直达

8）密度可达（Density-reachable）：对于 $\mathbf{x}_i$ 与 $\mathbf{x}_j$，若存在样本序列 $p_1,p_2,\cdots,p_m$，其中 $p_1=\mathbf{x}_i,p_m=\mathbf{x}_j$，且 $p_{i+1}$ 由 $p_{i}$ 密度直达，则称 $\mathbf{x}_j$ 由 $\mathbf{x}_i$ 密度可达

9）密度相连（Density-connected）：对于 $\mathbf{x}_i$ 与 $\mathbf{x}_j$，若存在 $\mathbf{x}_k$ 使得 $\mathbf{x}_i$ 与 $\mathbf{x}_j$ 均由 $\mathbf{x}_k$ 密度可达，则称 $\mathbf{x}_i$ 与 $\mathbf{x}_j$ 密度相连

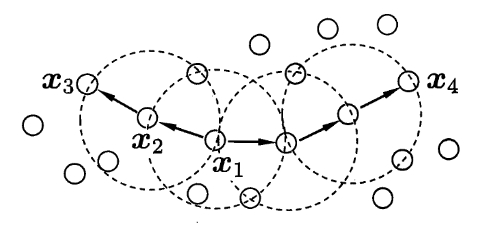
如下图所示，虚线展示出 $\epsilon$-邻域，$\mathbf{x}_1$ 是核心点，$\mathbf{x}_2$ 由 $\mathbf{x}_1$ 密度直达，$\mathbf{x}_3$ 由 $\mathbf{x}_1$ 密度可达，$\mathbf{x}_3$ 与 $\mathbf{x}_4$ 密度相连

【簇的定义】

基于上述的基本概念，DBSCAN 将簇定义为：由密度可达关系导出的最大的密度相连的样本集合

形式化来说，对于给定数据集 $D$ 和邻域参数 $(\epsilon,\text{MinPts})$，簇 $C\subseteq D$ 是满足以下性质的非空样本子集：

连接性（Connectivity）：$\mathbf{x}_i,\mathbf{x}_j\in C\rightarrow \mathbf{x}_i$ 与 $\mathbf{x}_j$ 密度相连
最大性（Maximality）：$\mathbf{x}_i\in C,\mathbf{x}_j$ 由 $\mathbf{x}_i$ 密度可达 $\rightarrow \mathbf{x}_j\in C$

【算法流程】

在由于簇的定义后，DBSACN 的核心就是如何从数据集 $D$ 中找出满足以上性质的簇

假设 $\mathbf{x}$ 为核心点，将由 $\mathbf{x}$ 密度可达的所有样本组成的集合记为：

$X = \{ \mathbf{x}'\in D | \mathbf{x}' 由 \mathbf{x} 密度可达 \}$

不难证明 $X$ 即为满足连接性和最大性的簇，故而可以先任选数据集中的一个核心对象为种子（seed），然后再从此出发确定相应的簇

也就是说，首先选择一个在其半径内至少有 $\text{minPts}$ 个的随机点，然后对核心点的邻域内的每个点进行评估，以确定它是否在 $\epsilon$ 距离内有 $\text{minPts}$

若该点满足 $\text{minPts}$ 标准，它将成为另一个核心点，集群将扩展，若不满足 $\text{minPts}$ 标准，它将成为边界点

随着过程的继续，算法开始发展成为核心点 $a$ 是 $b$ 的邻居，而 $b$ 又是 $c$ 的邻居，以此类推，当集群被边界点包围时，这个聚类簇已经搜索完全，因为在距离内没有更多的点

之后，选择一个新的随机点，并重复该过程以识别下一个簇

【sklearn 实现】

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现利用 DBSCAN 聚类

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
from scipy.spatial.distance import cdist
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    return X

# 数据标准化
def standard_scaler(X):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X) # 归一化，存有计算出的均值和方差
    X_std = scaler.transform(X) # 利用 scaler 进行标准化
    return X_std

# 模型训练
def train_model(features, eps, min_samples):
    # 建立聚类器
    model = DBSCAN(eps=eps, min_samples=min_samples)
    # 聚类
    model.fit(features)
    return model

# 可视化
def visualization(X, y):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

     # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
    # 数据处理
    X = deal_data()
    
    # 数据标准化
    X_std = standard_scaler(X)

    # 模型训练
    eps = 0.3
    min_samples = 10
    model = train_model(X_std, eps, min_samples)

    # 获取聚类标签
    label_pred = model.labels_

    # 可视化
    visualization(X_std, label_pred)