【概述】

聚类，是将数据集 $D$ 划分为若干互不相交的子集（样本簇），直观上来看，希望同一簇的样本尽可能的相似，不同簇的样本尽可能的不同，也就是说，聚类结果的簇内相似度（Intra-cluster Similarity）高，且簇间相似度（Inter-cluster Similarity）低

聚类问题的评价指标可划分为两类：

外部指标（Externa Index）：将聚类结果与某个参考模型进行比较
内部指标（Internal Index）：直接考察聚类结果而不利用任何参考模型

具体来说，参考模型就是训练样本的真实标签

本文仅介绍聚类问题的内部评价指标

【轮廓系数】

轮廓系数（Silhouette Coefficient）本质上衡量的是每个样本点到簇内样本的距离与其最近簇结构间距离的比值，该比值越小，说明该样本点所在的簇结构与其最近簇结构间的距离越远，说明聚类结果越好

对于聚类结果的轮廓系数来说，其实际上是每个样本点轮廓系数的平均值，即聚类样本中的每个样本点都对应一个轮廓系数值，总的轮廓系数则是所有样本点轮廓系数的平均值

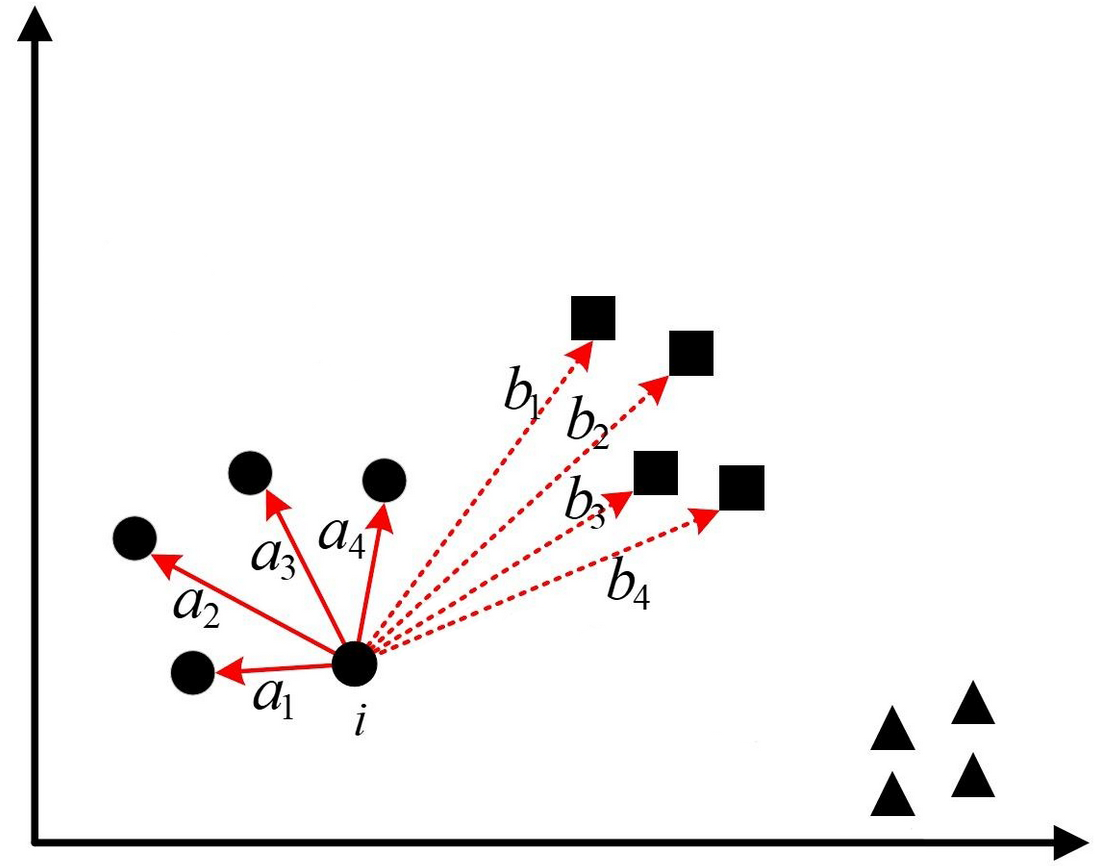
如上图所示，数据样本中一共有 $3$ 个簇结构，对于最左边圆形簇中的样本点来说，距离其最近的簇为中间方形的簇，现定义样本到簇中每个样本距离的均值为 $a(i)$，到最近簇中每个样本距离的均值为 $b(i)$，那么根据上图所示的结果有：

$\begin{gather*} a(i) = \frac{a_1+a_2+a_3+a_4}{4} \\ b(i) = \frac{b_1+b_2+b_3+b_4}{4} \end{gather*}$

需要注意的是，对于同一个簇中的每个样本点，距离自己最近的簇可能并不是同一个。同时，在寻找距离当前样本点最近的簇结构时，计算的是当前样本点到各个簇中心的最短距离，而不是计算当前样本点所在簇的簇中心到其它每个簇中心的最短距离

此时，样本 $i$ 的轮廓系数 $s(i)$ 被定义为：

$s(i) = \left\{\begin{array}{cc} 1-\frac{a(i)}{b(i)}, & a(i)<b(i) \\ 0, & a(i)=b(i) \\ \frac{b(i)}{a(i)}-1, & a(i)>b(i) \\ \end{array}\right.$

当 $a(i)$ 越小而 $b(i)$ 越大时，样本 $i$ 所在的簇中的簇内距离较小，那么可将样本 $i$ 到其它簇的距离近似地看作样本 $i$ 所在簇到其它簇之间的距离，进而可知样本 $i$ 所在的簇距离其最近簇的距离较远，所以 $s(i)$ 接近于 $1$，即聚类效果好
当 $b(i)$ 越小而 $a(i)$ 越大时，样本 $i$ 所在的簇的簇内距离较大，样本 $i$ 所在的簇距离其最近簇的距离较近，此时 $s(i)$ 接近于 $-1$，即聚类效果差
当样本 $i$ 所在的簇只有样本 $i$ 一个样本时，那么对于样本 $i$ 属于哪一个簇就不确定了，此时可粗略的认为其属于离它最近的簇中，故而有 $a(i)=b(i)$，即 $s(i)=0$

综上所述，可知 $s(i)$ 的取值范围是 $[-1,1]$，且 $s(i)$ 可进一步写为

$s(i) = \frac{b(i)-a(i)}{\max\{a(i),b(i)\}}$

故而，对于整个聚类结果而言，其轮廓系数为：

$s=\frac{1}{n} \sum_{i=1}^n s(i)$

其中，$n$ 为样本点的个数

【Calinski-Harabasz Index】

Calinski-Harabasz 指数的本质是簇间距离与簇内距离的比值，且整体计算过程与方差计算方式类似，所以又将其称之为方差比准则

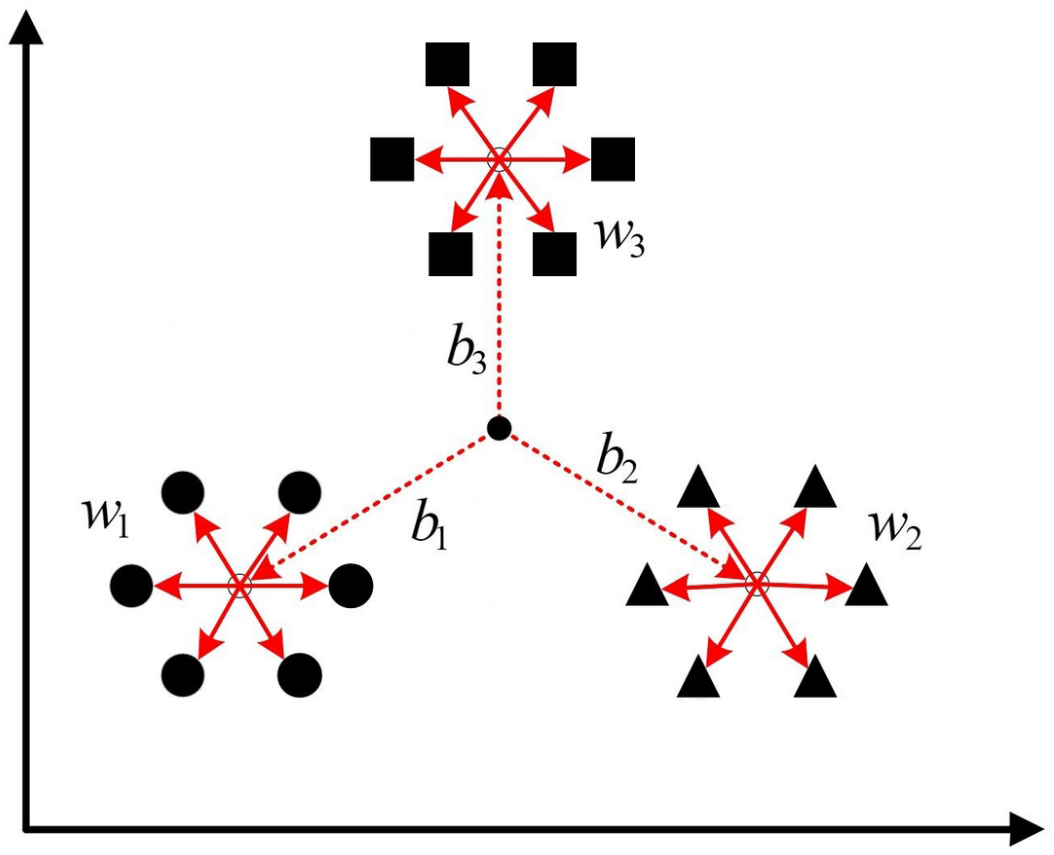
如上图所示，数据样本中一共有 $3$ 个簇结构，每个簇中有 $6$ 个样本点，且每个簇内部的白色圆点表示对应簇的簇中心，用 $w_k$ 表示第 $k$ 个簇的簇内距离和（每个样本点减去簇中心的平方和），用 $b_k$ 表示第 $k$ 个簇的簇中心到全局簇中心（所有样本点的中心）的加权距离

$\begin{gather*} w_k = \sum_{x\in C_k} (x-c_k)^2 \\ b_k = n_k (c_k - c)^2 \end{gather*}$

其中，$K$ 为簇的数量，$C_k$ 为第 $k$ 个簇中的所有样本，$c_k$ 为第 $k$ 个簇的簇中心，$c$ 为全局簇中心，$n_k$ 为第 $k$ 个簇中样本的数量

需要注意的是，在计算 $b_k$ 时，之所以要乘以每个簇对应的样本总数 $n_k$，是因为每个簇的簇中心到全局簇中心的距离只会计算一次，因此需要消除与簇内距离上的差异

Calinski-Harabasz 指数即所有簇内距离和与簇间距离和的比值，即：

$\begin{gather*} W = \sum_{k=1}^K w_k \\ B = \sum_{k=1}^K b_k \\ s = \frac{B}{K-1} / \frac{W}{n-K} = \frac{B}{W} \cdot \frac{n-K}{K-1} \end{gather*}$

其中，$n$ 为总样本数量，$s$ 的取值范围为 $(0,+\infty)$

根据上式可知，如果 $s$ 越大，则说明 $B$ 相对于 $W$ 越大，此时簇间距离便远大于簇内距离，即簇与簇之间相距较远，聚类结果好；反之，如果 $s$ 越小，则说明 $B$ 相对于 $W$ 越小，此时簇间距离远小于簇内距离，即簇与簇之间相距较近，聚类效果较差

【DB 指数】

DB 指数（Davies-Bouldin Index，DBI）是计算每个簇与之最相似簇之间相似度，然后再通过求得所有相似度的平均值来衡量整个聚类结果的优劣

DB 指数越高，即簇与簇之间的相似度越高，簇与簇之间的距离也就越小，那么此时聚类结果就越差，反之 DB 指数越低，即簇与簇之间的相似度越低，簇与簇之间的距离也就越大，那么此时聚类结果就越好

簇与簇之间的相似度被定义为两个簇的簇内直径和与簇间距离的比值，如上图所示，数据样本中一共有 $3$ 个簇结构，每个簇中有 $6$ 个样本点，且每个簇内部的白色圆点表示对应簇的簇中心，用 $\text{avg}(C_i)$ 表示第 $i$ 个簇的样本平均距离，$D_{\text{cen}}(C_i,C_j)$ 表示第 $i$ 个簇和第 $j$ 个簇的中心距离

此时，簇 $C_i$ 与簇 $C_j$ 间的相似度为：

$R_{ij} = \frac{\text{avg}(C_i)+\text{avg}(C_j)}{D_{\text{cen}}(C_i,C_j)}$

进一步，DB 指数被定义为：

$DBI = \frac{1}{K} \sum_{i,j=1}^{K} \max_{i\neq j} R_{ij}$

其中，$K$ 为簇的个数

从上式可以看出，对于第 $i$ 个簇的相似度来说，其等于 $R_{i1},R_{i2},\cdots,R_{iK}$ 中的最大值，而在计算 $R_{ij}$ 的过程中，$\text{avg}(C_i)$ 一直是保持不变的，同时如果要取 $R_{ij}$ 的最大值，$\text{avg}(C_j)$ 要尽可能大，$D_{\text{cen}}(C_i,C_j)$ 要尽可能小，这意味着簇 $C_j$ 中的样本点分布要尽可能离散，且簇 $C_i$ 和簇 $C_j$ 尽可能接近，对应的就是聚类结果较差

因此，$R_{ij}$ 越大，说明两个簇相距越近，越相似，故而 DB 指数越大反映的是聚类结果越差，越小则是聚类结果越好