【概述】

聚类，是将数据集 $D$ 划分为若干互不相交的子集（样本簇），直观上来看，希望同一簇的样本尽可能的相似，不同簇的样本尽可能的不同，也就是说，聚类结果的簇内相似度（Intra-cluster Similarity）高，且簇间相似度（Inter-cluster Similarity）低

聚类问题的评价指标可划分为两类：

外部指标（Externa Index）：将聚类结果与某个参考模型进行比较
内部指标（Internal Index）：直接考察聚类结果而不利用任何参考模型

具体来说，参考模型就是训练样本的真实标签

本文仅介绍聚类问题的外部评价指标

【聚类纯度】

聚类纯度（Cluster Purity）是最简单直观的外部指标，其基本思想与分类的准确率类似，用聚类正确的样本数除以总的样本数，因此它也经常被称为聚类的准确率

但由于并不知道聚类结果中每个簇所对应的真实类别，因此需要取每种情况下的最大值，其计算公式如下：

$P=\frac{1}{n} \sum_{k=1}^K \max_{c_j\in \mathbb{C}} |\omega_k\cap c_j|$

其中，$n$ 为样本总数，$K$ 为聚类簇数，$\omega_k$ 代表聚类后第 $k$ 个簇中的所有样本，$\mathbb{C}=\{c_1,c_2,\cdots,c_J\}$ 是正确的类别，$c_{j}$ 表示第 $j$ 个类别中真实的样本

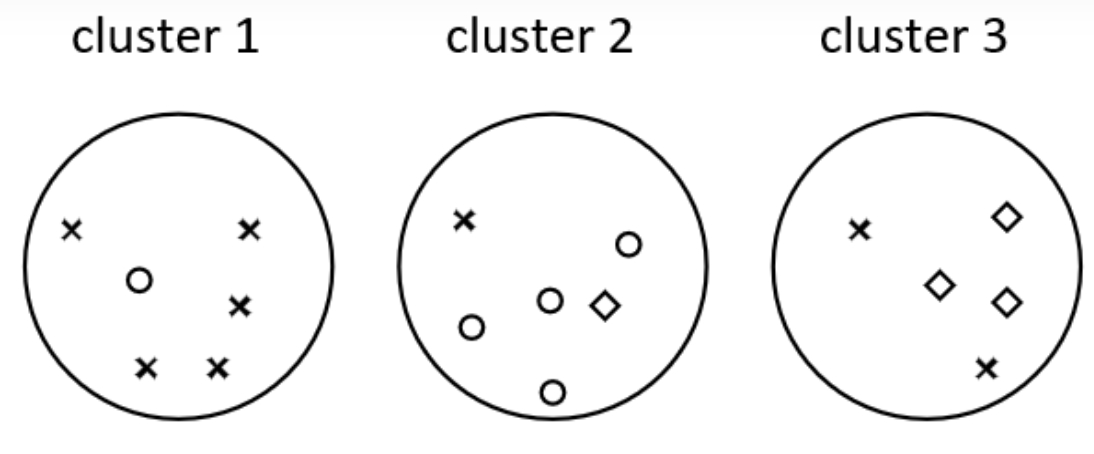
如上图所示，定义 $\mathbb{C}=\{c_1,c_2,c_3\}$，其中 $c_1$ 表示叉形，$c_2$ 表示圆形，$c_3$ 表示菱形，那么对于第一个簇来说，有：

$\begin{gather*} |\omega_1 \cap c_1| = 5 \\ |\omega_1 \cap c_2| = 1 \\ |\omega_1 \cap c_3| = 0 \end{gather*}$

则：

$\max_{c_j\in \mathbb{C}}|\omega_k\cap c_j|=5$

同理，可得到第二个簇、第三个簇中最大的 $|\omega_k\cap c_j|$ 分别是 $4,3$，故最终纯度为：

$P = \frac{5+4+3}{17} = 0.706$

【匹配矩阵】

对于数据集 $D=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\}$，第 $i$ 个样本 $\mathbf{x}_i$ 有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^m$，假定通过聚类方法给出的簇划分为 $\mathcal{C} = \{C_1,C_2,\cdots,C_k\}$，实际类别划分为 $\mathcal{C}^{*}=\{C^{*}_1,C^{*}_2,\cdots,C^{*}_s\}$，通常 $k\neq s$

相应地，令 $\boldsymbol{\lambda}$ 和 $\boldsymbol{\lambda}^{*}$ 分别表示 $\mathcal{C}$ 和 $\mathcal{C}^{*}$ 对应的簇标记向量，定义：

$\begin{array}{cc} TP = |SS|,& SS=\{ (\mathbf{x}_i,\mathbf{x}_j) | \lambda_i=\lambda_j, \lambda_i^{*}=\lambda_j^{*}, i<j \} \\ FP = |SD|,& SD=\{ (\mathbf{x}_i,\mathbf{x}_j) | \lambda_i=\lambda_j, \lambda_i^{*}\neq\lambda_j^{*}, i<j \} \\ TN = |DD|,& DD=\{ (\mathbf{x}_i,\mathbf{x}_j) | \lambda_i\neq\lambda_j, \lambda_i^{*}\neq\lambda_j^{*}, i<j \} \\ FN = |DS|,& DS=\{ (\mathbf{x}_i,\mathbf{x}_j) | \lambda_i\neq\lambda_j, \lambda_i^{*}=\lambda_j^{*}, i<j \} \\ \end{array}$

其中，四个集合包含的元素如下：

集合 $SS$：包含了在 $\mathcal{C}$ 中隶属于相同簇，在 $\mathcal{C}^{*}$ 中隶属于相同类别的样本对 $(\mathbf{x}_i,\mathbf{x}_j)$
集合 $SD$：包含了在 $\mathcal{C}$ 中隶属于相同簇，在 $\mathcal{C}^{*}$ 中隶属于不同类别的样本对 $(\mathbf{x}_i,\mathbf{x}_j)$
集合 $DD$：包含了在 $\mathcal{C}$ 中隶属于不同簇，在 $\mathcal{C}^{*}$ 中隶属于不同类别的样本对 $(\mathbf{x}_i,\mathbf{x}_j)$
集合 $DS$：包含了在 $\mathcal{C}$ 中隶属于不同簇，在 $\mathcal{C}^{*}$ 中隶属于相同类别的样本对 $(\mathbf{x}_i,\mathbf{x}_j)$

此时，即可得到聚类下的匹配矩阵（Confusion Matrix），即：

	同一簇	不同簇
同一类	TP	FN
不同类	FP	TN

由于每个样本对 $(\mathbf{x}_i,\mathbf{x}_j),i<j$ 仅能在一个集合中出现，故有：

$TP+FP+TN+FN = \tbinom{n}{2} = \frac{n(n-1)}{2}$

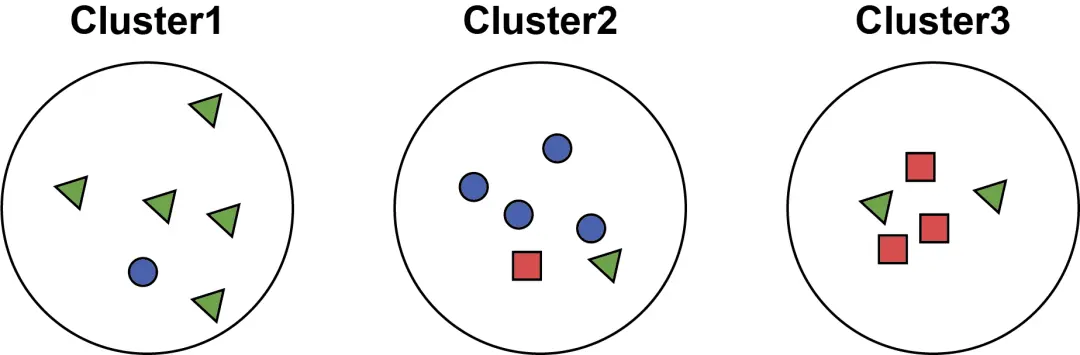
如图所示，聚类簇数为 $3$，实际类别划分为绿色三角形、蓝色圆形、红色正方形，下面计算 TP、FP、TN、FN

对于 TP 的计算，其是在第一簇中的 $5$ 个绿色三角形中取 $2$ 个、在第二簇的 $4$ 个蓝色圆形中取 $2$ 个、在第三簇的 $3$ 个红色正方形中取 $2$ 个、在第三簇的 $2$ 个绿色三角形中取 $2$ 个，这四种情况的和，即：

$TP = \tbinom{5}{2} + \tbinom{4}{2} + \tbinom{3}{2} + \tbinom{2}{2} = 10+6+3+1=20$

而对于 FP、TN、FN 的计算较为复杂，但可以转变思路，进行联合计算

TP+FP 是在同一簇中取两个样本，即：

$TP+FP = \tbinom{6}{2} + \tbinom{6}{2} + \tbinom{5}{2} = 15+15+10=40$

TP+FN 是在任意两个同类样本点分布在同簇和非同簇的情况和，即：

$TP+FN = \tbinom{8}{2}+\tbinom{5}{2}+\tbinom{4}{2} = 28+10+6 = 44$

TP+FP+TN+FN 是在所有样本中随机抽取两个样本，即：

$TP+FP+TN+FN = \tbinom{17}{2} = 136$

根据这些组合结果与 TP 的值，即可得到匹配矩阵的所有结果，即：

	同一簇	不同簇
同一类	TP(20)	FN(24)
不同类	FP(20)	TN(72)

【常见指标】

基于匹配矩阵，可得出如下常用的聚类外部评价指标

兰德指数

兰德指数（Rand Index，RI）的计算公式如下：

$RI = \frac{TP+TN}{TP+TN+FP+FN}$

其取值范围在 $[0,1]$ 区间内，值越大说明聚类结果越接近参考模型

从形式上看，兰德指数与分类问题中的准确率十分相似，但两者有着本质的区别

$F_{\beta}$ 分数

$F_{\beta}$ 分数（F-Score）的计算公式如下：

$F_{\beta} = (1+\beta^2) \frac{P\cdot R}{\beta^2\cdot P+R}, \beta>0$

其中，$P$、$R$ 的计算如下

$\begin{gather*} P = \frac{TP}{TP+FP} \\ R = \frac{TP}{TP+FN} \\ \end{gather*}$

从形式上看，$F_{\beta}$ 分数与分类问题中的 $F_{\beta}$ 分数十分相似，但两者有着本质的区别

杰卡德系数

Jaccard 系数（Jaccard Coefficient，JC）的计算公式如下：

$JC = \frac{TP}{TP+FP+FN}$

FM 指数

FM 指数（Fowlkes and Mallows Index，FMI）的其计算公式如下：

$FMI = \sqrt{\frac{TP}{TP+FP} \cdot \frac{TP}{TP+FN}}$