PageRank

【概述】

PageRank 算法于 1996 年由 Page 和 Brin 提出，最初用于谷歌搜索引擎的网页排序，其是定义在网页集合上的一个函数，其对每个网页给出一个正实数，表示网页的重要程度，整体构成一个向量，PageRank 值越高，网页越重要，在互联网搜索的排序中可能就被排在前面

PageRank 假设互联网是一个有向图，每个网页是图中的一个结点，浏览者在每个网页依照连接出去的超链接以等概率跳转到下一个网页，并持续不断进行这样的随机跳转，整个沿着有向图随机访问各网页结点的过程，被定义成一个随机游走模型，即一阶马尔可夫链

在一定条件下，极限情况访问每个结点的概率收敛到平稳分布，此时各个结点的 PageRank 值就是平稳概率，表示结点的重要度

如下图所示，结点 A、B、C、D 表示网页，结点间的有向边表示网页间的超链接，边权表示网页间随机跳转的概率。假设有一个浏览者在网上随机游走，若其在网页 A，则下一步有 $\frac{1}{3}$ 的概率转移到网页 B、C、D；若其在网页 B，则下一步有 $\frac{1}{2}$ 的概率转移到网页 A、D；若在网页 C，则下一步以概率 $1$ 转移到网页 A；若在网页 D，则下一步以 $\frac{1}{2}$ 的概率转移到网页 B、C

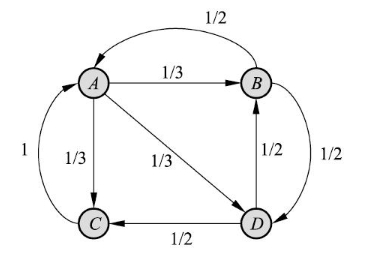
直观来看，对于一个网页来说，如果指向这个网页的超链接越多，随机跳转到该网页的概率也就越大，该网页的 PageRank 值也就越高，这个网页也就越重要

PageRank 值依赖于网络的拓扑结构，一旦网络的拓扑关系确定，PageRank 值也随之确定，其计算通常是一个迭代过程，即先假设一个初始分布，通过迭代不断计算所有网页的 PageRank 值，直到收敛为止

【定义】

有向图的随机游走模型

给定一个含 $n$ 个结点的有向图，在这个有向图上定义随机游走模型，即一阶马尔可夫链，其中结点表示状态，有向边表示状态间的转移

假设从一个结点到通过有向边相连的所有结点的转移概率相等，则转移矩阵是一个 $n$ 阶矩阵：

$$M=[m_{ij}]_{n\times n}$$

其中，第 $i$ 行第 $j$ 列的元素 $m_{ij}$ 取值规则为：若结点 $j$ 有 $k$ 个有向边连出，且结点 $i$ 是其连出的一个结点，则 $m_{ij}=\frac{1}{k}$，否则 $m_{ij}=0$​

在下图所示的有向图中，可以定义随机游走模型，即转移矩阵为：

$$M=\begin{bmatrix} 0 & \frac{1}{2} & 1 & 0 \\ \frac{1}{3} & 0 & 0 & \frac{1}{2} \\ \frac{1}{3} & 0 & 0 & \frac{1}{2} \\ \frac{1}{3} & \frac{1}{2} & 0 & 0 \\ \end{bmatrix}$$

转移矩阵的每个元素非负，且每列元素和为 $1$，其是一个随机矩阵，即：

$$\begin{gather*} m_{ij} \geq 0 \\ \sum_{i=1}^n m_{ij}=1 \end{gather*}$$

在有向图上随机游走形成马尔可夫链，即游走者每经过一个单位时间转移一个状态，若当前时刻在第 $j$ 个状态（结点），那么下一个时刻在第 $i$ 个状态（结点）的概率是 $m_{ij}$，这一概率只依赖于当前状态，与过去无关，即具有马尔可夫性

随机游走在某时刻 $t$ 访问各个结点的概率分布就是马尔可夫链在时刻 $t$ 的状态分布，可用一个 $n$ 维列向量 $R_t$ 表示，那么在 $t+1$ 时刻访问各结点的概率分布 $R_{t+1}$ 满足：

$$R_{t+1}=MR_t$$

PageRank 的基本定义

给定一个包含 $n$ 个结点 $v_1,v_2,\cdots,v_n$ 的强连通且非周期的有向图，在其基础上定义随机游走模型，假设转移矩阵为 $M$，且从一个结点到其连出的所有结点的转移概率相等，那么在时刻 $0,1,2,\cdots,t,\cdots$ 访问各个结点的概率分布为：

$$R_0,MR_0,M^2R_0,\cdots,M^tR_0,\cdots$$

根据马尔可夫链平稳分布定理：不可约且非周期的有限状态马尔可夫链，有唯一平稳分布存在，且当时间趋于无穷时，状态分布收敛于唯一的平稳分布，即极限 $\lim\limits_{t\rightarrow\infty} M^tR_0=R$ 存在，且极限向量 $R$ 表示马尔可夫链的平稳分布，并满足：

$$MR=R$$

其中，平稳分布 $R$ 即这个有向图的 PageRank，$R$ 的各个分量被称为各个结点的 PageRank 值

$$R=\begin{bmatrix} PR(v_1) \\ PR(v_2) \\ \vdots \\ PR(v_n) \end{bmatrix}$$

其中，$PR(v_i)$ 表示结点 $v_i$ 的 PageRank 值

对于 $i=1,2,\cdots,n$，有：

$$\begin{gather*} PR(v_i) \geq 0 \\ \sum_{i=1}^n PR(v_i) = 1 \\ PR(v_i) = \sum_{v_j \in M(v_i)} \frac{PR(v_j)}{L(v_j)} \end{gather*}$$

其中，$M(v_i)$ 表示指向结点 $v_i$ 的结点集合，$L(v_j)$ 表示结点 $v_j$ 连出有向边的个数

---

在下图所示的有向图中，根据 PageRank 的基本定义，可以求出相应的 PageRank 值

易得，转移矩阵：

$$M=\begin{bmatrix} 0 & \frac{1}{2} & 1 & 0 \\ \frac{1}{3} & 0 & 0 & \frac{1}{2} \\ \frac{1}{3} & 0 & 0 & \frac{1}{2} \\ \frac{1}{3} & \frac{1}{2} & 0 & 0 \\ \end{bmatrix}$$

假设初始时访问各结点的概率相等，即初始分布向量 $R_0$ 为：

$$R_0 = \begin{bmatrix} \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \end{bmatrix}$$

将转移矩阵 $M$ 连乘初始向量 $R_0$ 可得向量序列：

$$\begin{bmatrix} \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \end{bmatrix},\begin{bmatrix} \frac{9}{24} \\ \frac{5}{24} \\ \frac{5}{24} \\ \frac{5}{24} \\ \end{bmatrix},\begin{bmatrix} \frac{15}{48} \\ \frac{11}{48} \\ \frac{11}{48} \\ \frac{11}{48} \\ \end{bmatrix},\begin{bmatrix} \frac{11}{32} \\ \frac{7}{32} \\ \frac{7}{32} \\ \frac{7}{32} \\ \end{bmatrix},\cdots,\begin{bmatrix} \frac{3}{9} \\ \frac{2}{9} \\ \frac{2}{9} \\ \frac{2}{9} \\ \end{bmatrix},\cdots$$

最终可得极限向量：

$$R = \begin{bmatrix} \frac{3}{9} \\ \frac{2}{9} \\ \frac{2}{9} \\ \frac{2}{9} \\ \end{bmatrix}$$

即有向图的 PageRank 值

PageRank 的一般定义

PageRank 的基本定义是理想化的情况，在这种情况下，PageRank 存在，且可以通过不断迭代求得 PageRank 值，但现实中一般的有向图未必满足强连通且非周期的条件，随着时间步 $t$ 的推移，访问各结点的概率将变为 $0$，因此 PageRank 的基本定义并不适用于现实情况

基于现实情况的考虑，PageRank 的一般定义是在基本定义的基础上导入平滑项，即给定一个包含 $n$ 个结点 $v_1,v_2,\cdots,v_n$ 的任意有向图，在其基础上定义随机游走模型，假设转移矩阵为 $M$，且从一个结点到其连出的所有结点的转移概率相等

由于这个马尔可夫链未必具有平稳分布，因此假设另一个完全随机游走的模型，其转移矩阵的元素全部为 $\frac{1}{n}$，即从任意一个结点到任意一个结点的转移概率均为 $\frac{1}{n}$，将两个转移矩阵进行线性组合，即构成一个新的转移矩阵，在其上可以定义一个新的马尔可夫链，容易证明这个马尔可夫链一定具有平稳分布，且平稳分布满足：

$$R=dMR+\frac{1-d}{n} \mathbf{1}$$

其中，第一项表示状态分布是平稳分布时依照转移矩阵 $M$ 访问各个结点的概率，第二项称为平滑项，表示完全随机访问各个结点的概率，保证所有 PageRank 的值都不会为 $0$，$0< d< 1$ 是为阻尼因子（Damping Factor），其取值由经验决定，当 $d$ 接近 $1$ 时，随机游走依照转移矩阵 $M$ 进行，当 $d$ 接近 $0$​ 时，随机游走以等概率随机访问各个结点

$\mathbf{1}$ 是所有分量为 $1$ 的 $n$ 维向量，平稳分布 $R$ 即这个有向图的 PageRank，$R$ 的各个分量被称为各个结点的 PageRank 值

$$R=\begin{bmatrix} PR(v_1) \\ PR(v_2) \\ \vdots \\ PR(v_n) \end{bmatrix}$$

其中，$PR(v_i)$ 表示结点 $v_i$ 的 PageRank 值

对于 $i=1,2,\cdots,n$，有：

$$\begin{gather*} PR(v_i) \geq 0 \\ \sum_{i=1}^n PR(v_i) = 1 \\ PR(v_i) = d\Big( \sum_{v_j \in M(v_i)} \frac{PR(v_j)}{L(v_j)} \Big) + \frac{1-d}{n} \end{gather*}$$

其中，$M(v_i)$ 表示指向结点 $v_i$ 的结点集合，$L(v_j)$ 表示结点 $v_j$​ 连出有向边的个数

一般的 PageRank 定义意味着浏览者将按照以下规则在网上随机游走：在任意一个网页上，浏览者以概率 $d$ 决定按照按照超链接随机跳转，此时以等概率从连接出去的超链接跳转到下一个网页，或者以概率 $1-d$ 决定完全随机跳转，此时以等概率 $\frac{1}{n}$ 跳转到任意一个网页

【计算】

PageRank 的定义是构造性的，即定义本身就给出了算法，其常用的计算方法包括：迭代算法、幂法、代数算法

迭代算法

PageRank 的迭代算法就是按照 PageRank 的一般定义进行迭代，直到收敛，即：

$$R_{t+1}=dMR_t+\frac{1-d}{n} \mathbf{1}$$

---

输入：含有 $n$ 个结点的有向图，转移矩阵 $M$，阻尼因子 $d$，初始向量 $R_0$

输出：任意有向图 PageRank 向量 $R$

算法流程：

Step 1：令 $t=0$

Step 2：计算

$$R_{t+1}=dMR_t+\frac{1-d}{n} \mathbf{1}$$

Step 3：若 $R_{t+1}$ 和 $R_t$ 充分接近，令 $R=R_{t+1}$，停止迭代

Step 4：令 $t=t+1$，执行 Step 2

幂法

幂法主要用于近似计算矩阵的主特征值和主特征向量，按照 PageRank 的一般定义，其可以改写为：

$$R=\Big(dM+\frac{1-d}{n} E\Big)R = AR$$

其中，$0< d< 1$ 为阻尼因子，$E$ 是所有元素为 $1$ 的 $n$ 阶方阵，根据 Perron-Frobenius 定理，一般 PageRank 的向量 $R$ 是矩阵 $A$ 的主特征向量，主特征值是 $1$，因此可以采用幂法来近似计算一般 PageRank

---

输入：含有 $n$ 个结点的有向图，转移矩阵 $M$，阻尼因子 $d$，初始向量 $\mathbf{x}_0$，计算精度 $\varepsilon$

输出：任意有向图 PageRank 向量 $R$

算法流程：

Step 1：令 $t=0$，选择初始向量 $\mathbf{x}_0$

Step 2：计算有向图的一般转移矩阵 $A$

$$A=dM+\frac{1-d}{n}E$$

Step 3：迭代并规范化结果向量

$$\begin{gather*} \mathbf{y}_{t+1} = A\mathbf{x}_t \\ \mathbf{x}_{t+1} = \frac{\mathbf{y}_{t+1}}{\Vert \mathbf{y}_{t+1}\Vert} \\ \end{gather*}$$

Step 4：当 $\Vert \mathbf{x}_{t+1}-\mathbf{x}_t \Vert < \varepsilon$ 时，令 $R=\mathbf{x}_t$，停止迭代

Step 5：令 $t=t+1$，执行 Step 3

Step 6：对 $R$ 规范化处理，使其表示概率分布

代数算法

代数算法通过一般转移矩阵的逆矩阵计算有向图的一般 PageRank

根据一般 PageRank 的定义：

$$R=dMR+\frac{1-d}{n} \mathbf{1}$$

有：

$$(I-dM)R=\frac{1-d}{n} \mathbf{1}$$

即得：

$$R=(I-dM)^{-1}\frac{1-d}{n}\mathbf{1}$$

其中，$I$ 是单位矩阵，当 $0<d<1$ 时，$R$ 的解存在且唯一，这样可以通过求逆矩阵 $(I-dM)^{-1}$ 得到有向图的一般 PageRank