Alex_McAvoy

想要成为渔夫的猎手

多层感知机

发表于 分类于 ， ，
本文字数： 6.6k 阅读时长 ≈ 6 分钟

【引入】

在 单层感知机 中，介绍了单层感知机模型：

其可以处理线性可分的二分类问题

与（AND）、或（OR）、非（NOT）均可认为是一线性可分问题，即这三种逻辑电路均可使用单层感知机来实现

而对于异或（XOR）来说，其是一个线性不可分问题，无法使用单层感知机来实现，考虑到异或可以通过与、或、非来组合实现：

那么，借鉴这种思想，将多个感知机进行连接，形成层级结构，由此有了多层感知机（Muti-Layer Perceptron，MLP）

【从与或非到异或】

与门

与门，是具有两个输入和一个输出的门电路，在两个输入均为 $1$ 时输出 $1$，其他情况输出 $0$

其真值表如下：

$x_1$ $x_2$ $y$
$0$ $0$ $0$
$0$ $1$ $0$
$1$ $0$ $0$
$1$ $1$ $1$

若想使用感知机来表示与门，需要做的就是确定参数 $\omega_1,\omega_2$ 与阈值 $\theta$，使得在给定二值输入时，感知机的输出能够满足真值表

满足真值表条件的参数的选择方案有无数种，这里选取较为简单的一种，即：

此时，有：

仅当 $x_1=x_2=1$ 时，有 $y=1$

其分离超平面如下：

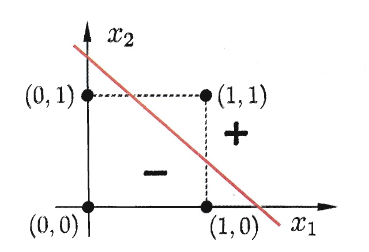
或门

或门，是具有两个输入和一个输出的门电路，在两个输入中的任意一个为 $1$ 时输出 $1$，在两个输入全为 $0$ 时输出 $0$

其真值表如下：

$x_1$ $x_2$ $y$
$0$ $0$ $0$
$0$ $1$ $1$
$1$ $0$ $1$
$1$ $1$ $1$

若想使用感知机来表示或门，需要做的就是确定参数 $\omega_1,\omega_2$ 与阈值 $\theta$，使得在给定二值输入时，感知机的输出能够满足真值表

满足真值表条件的参数的选择方案有无数种，这里选取较为简单的一种，即：

此时，有：

当 $x_1=1$ 或 $x_2=1$ 时，有 $y=1$

其分离超平面如下：

非门

非门，是具有一个输入和一个输出的门电路，在输入为 $1$ 时输出 $0$，输入为 $0$ 时输出 $1$

其真值表如下：

$x$ $y$
$0$ $1$
$1$ $0$

若想使用感知机来表示非门，需要做的就是确定参数 $\omega$ 与阈值 $\theta$，使得在给定输入时，感知机的输出能够满足真值表

满足真值表条件的参数的选择方案有无数种，这里选取较为简单的一种，即：

此时，有：

当 $x=1$ 时，有 $y=0$；当 $x=0$ 时，有 $y=1$

其分离超平面如下：

异或门

异或门，是具有两个输入和一个输出的门电路，在两个输入相同时输出 $0$，在两个输入不同时输出 $1$

其真值表如下：

$x_1$ $x_2$ $y$
$0$ $0$ $0$
$0$ $1$ $1$
$1$ $0$ $1$
$1$ $1$ $0$

其分离超平面如下：

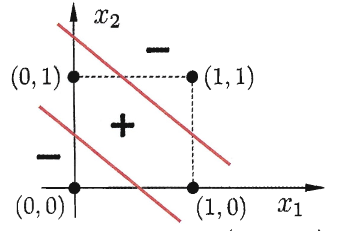
可以看出，若想将其分开，只能通过如下图的曲线来分割

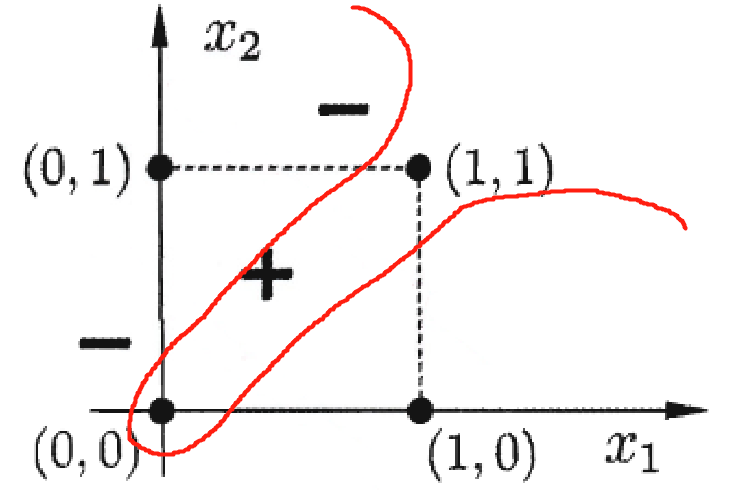
可以发现，异或问题是一个非线性可分问题，单层感知机无法进行实现

在数字电路中，异或门可以通过与门、非门、或门的组合来实现

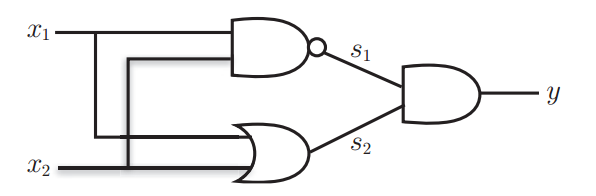
根据上面的数字电路图，给出真值表：

$x_1$ $x_2$ $s_1$ $s_2$ $y$
$0$ $0$ $1$ $0$ $0$
$0$ $1$ $1$ $1$ $1$
$1$ $0$ $1$ $1$ $1$
$1$ $1$ $0$ $1$ $0$

那么，参考真值表，可以构建出如下由 MP 神经元构成的网络图，即最简单的多层感知机

其中，第 $0$ 层为输入层（Input Layer），该层不涉及到计算；第 $1$ 层用于处理数据，被称为隐藏层（Hidden Layer），第 $2$ 层为输出层（Output Layer），将隐藏层的输出进行处理，作为整个多层感知机的输出

【多层感知机】

多层感知机（Multi-Layer Perceptron，MLP），也叫人工神经网络（Artificial Neural Network，ANN），是最简单的神经网络结构，其除了输入层和输出层外，中间可以有多个隐藏层，最简单的 MLP 只包含一个隐藏层

如上图所示的多层感知机，每层神经元与下一层神经元完全互连，且神经元间不存在同层连接与跨层连接，这样的神经网络结构被称为多层前馈神经网络（Multi-layer Feedforward Neural Networks）

对于多层前馈神经网络来说，输入层用于接收外接输入，隐藏层与输出层对输入进行处理，并由输出层输出，因此，上图所示的多层感知机，其层数为 $2$，一般称为两层网络

第 $0$ 层为输入层，该层不涉及到计算；第 $1$ 层为隐藏层，含有 $5$ 个 MP 神经元；第 $2$ 层为输出层，含有 $3$ 个 MP 神经元

设第 $1$ 层权重为 $W_h$，阈值为 $\theta_h$，激活函数为 $f(\cdot)$，则该多层感知机隐藏层的输出为：

设第 $2$ 层权重为 $W_o$，阈值为 $\theta_o$，则该多层感知机的输出为：

将上述两个式子联立，可得：

在分类问题中，通常会将输出层的输出单元个数设为 $1$ ，并对输出 $O$ 进行 softmax 运算，将输出转换为分类概率

多层感知机的学习过程，就是根据训练数据来调整神经元间的连接权重以及每个神经元的阈值，除了使用随机梯度下降法、牛顿法等迭代算法外，由于多层感知机是最基础的神经网络，其还可使用 BP 算法训练

关于 BP 算法，详见：BP 神经网络与反向传播算法

【sklearn 实现】

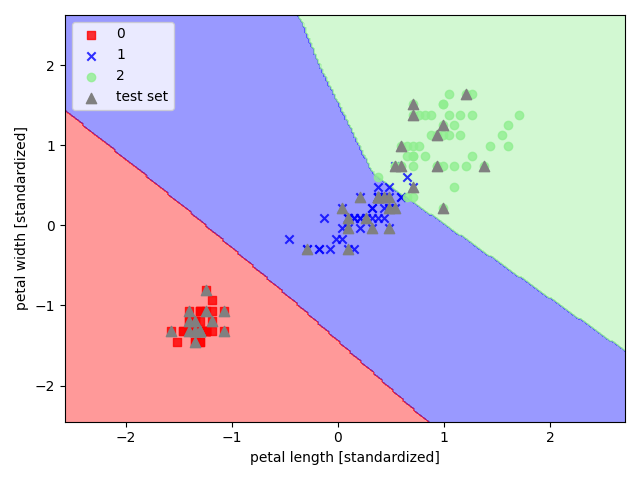
以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现多层感知机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target  #取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train,X_test):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 模型训练
def train_model(X_train_std, y_train):
    # 建立MLP模型，优化算法采用L-BFGS
    # solver可选：
    #  - lbfgs：L-BFGS，在小数据上表现较好
    #  - adam：Adam，鲁棒性较好
    #  - sgd：SGD，在参数调整较优时会有最佳表现
    model = MLPClassifier(solver='lbfgs', alpha=1e-5,hidden_layer_sizes=(30,20), random_state=1)
    # 训练
    model.fit(X_train_std, y_train)
    return model

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵，三分类情况下，大小为 3*3
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # macro 分类报告
    macro_class_report = classification_report(y_test, y_pred,target_names=["类0","类1","类2"])
    # 微精确率
    micro_p = precision_score(y_test,y_pred,average='micro') 
    # 微召回率
    micro_r = recall_score(y_test,y_pred,average='micro')
    # 微F1得分
    micro_f1 = f1_score(y_test,y_pred,average='micro') 
    
    indicators = {"cm2":cm2,"acc":acc,"acc_num":acc_num,"macro_class_report":macro_class_report,"micro_p":micro_p,"micro_r":micro_r,"micro_f1":micro_f1}
    return indicators

# 可视化
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 绘制决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 #第一个特征取值范围作为横轴
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 #第二个特征取值范围作为纵轴
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) # reolution为网格剖分粒度
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) # 对组合的特征进行预测，ravel为数组展平
    Z = Z.reshape(xx1.shape) # Z是列向量
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) # x和y为两个等长一维数组，z为二维数组，指定每一对xy所对应的z值
    plt.xlim(xx1.min(), xx1.max()) #对等高线间的区域进行填充
    plt.ylim(xx2.min(), xx2.max()) #对等高线间的区域进行填充
    
    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0, c='gray', marker='^', linewidths=1, s=55, label='test set')
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()
    
if __name__ == "__main__":
    # 特征提取
    X, y = deal_data()
    
    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
    
    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)
    
    # 模型训练
    model = train_model(X_train_std, y_train)
    
    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test) # 测试集y值
    print("y pred:", y_pred) # 预测y值
    
    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"] 
    print("混淆矩阵：\n", cm2) 
    acc =  indicators["acc"]
    print("准确率：", acc)
    acc_num =  indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    macro_class_report = indicators["macro_class_report"]
    print("macro 分类报告：\n", macro_class_report)
    micro_p = indicators["micro_p"]
    print("微精确率：", micro_p)
    micro_r = indicators["micro_r"]
    print("微召回率：", micro_r)
    micro_f1 = indicators["micro_f1"]
    print("微F1得分：", micro_f1)
    
    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(105, 150))
感谢您对我的支持，让我继续努力分享有用的技术与知识点！