对数线性回归与广义线性模型

【对数线性回归】

对于给定的容量为 $n$ 的训练集 $D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x_i}=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出为 $y_i$，多元线性回归学习到的模型为 $f(\mathbf{x_i};\boldsymbol{\theta})$，使得 $f(x_i;\boldsymbol{\theta})\simeq y_i$

假设函数 $f(\mathbf{x_i};\boldsymbol{\theta})$ 形式如下：

$$f(\mathbf{x_i};\boldsymbol{\theta})=\theta^{(0)} + \theta^{(1)} x_i^{(1)} + \theta^{(2)} x_i^{(2)} + ... + \theta^{(m)} x_i^{(m)}$$

其中，特征参数 $\boldsymbol{\theta}$ 为 $(m+1)\times 1$ 的列向量，即：

$$\boldsymbol{\theta}=[\theta^{(0)},\theta^{(1)},...,\theta^{(m)}]^T\in \mathbb{R}^{m+1}$$

为了表述方便，对假设函数进行简化，定义一个额外的第 $0$ 个特征量，这个特征量对所有样本的取值全部为 $1$，这使得特征量从过去的 $m$ 个变为 $m+1$ 个，即设：$x_i^{(0)}=1$

那么假设函数就可以写为：

$$f(\mathbf{x_i};\boldsymbol{\theta})=\theta^{(0)} x_i^{(0)} + \theta^{(1)} x_i^{(1)} + \theta^{(2)} x_i^{(2)} + ... + \theta^{(m)} x_i^{(m)}$$

将数据集 $D$ 写为 $(m+1)\times n$ 的矩阵，即：

$$X=\begin{bmatrix} x_{1}^{(0)} & x_{2}^{(0)} & ... & x_{n}^{(0)} \\ x_{1}^{(1)} & x_{2}^{(1)} & ... & x_{n}^{(1)} \\ \vdots & \vdots & \ddots & \vdots \\ x_{1}^{(m)} & x_{2}^{(m)} & ... & x_{n}^{(m)} \end{bmatrix}$$

同时，将预测值 $\hat{y_i}$ 也写为矩阵形式，即预测输出变量 $\hat{Y}$ 为 $n\times 1$ 的列向量：

$$\hat{Y}=[\hat{y_1},\hat{y_2},...,\hat{y_n}]^T \in \mathbb{R}^{n}$$

那么，多元线性回归模型就可写为：

$$\hat{Y}=\boldsymbol{\theta}^TX$$

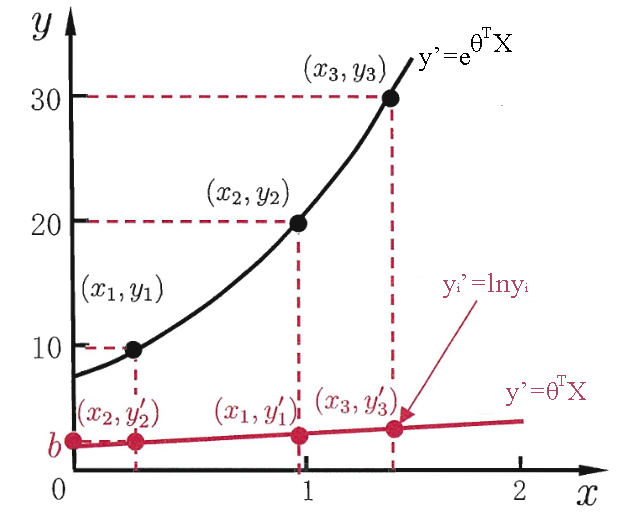
当给定输入值后，如果希望预测值能够逼近真实值 $y_i$ 的衍生物，即输出是在指数尺度上变化时，就可将输出的对数作为线性模型逼近的目标，即：

$$\ln \hat{Y}=\boldsymbol{\theta}^TX$$

这就是对数线性回归（Log-linear Regression），实际上是试图让 $e^{\boldsymbol{\theta}^TX}$ 逼近真实输出 $\hat{Y}$

对数线性回归形式上虽然仍是线性回归，但其实质上是在求取输入空间到输出空间的非线性函数的映射

【广义线性模型】

更一般地，考虑单调可微函数 $g(\cdot)$，令：

$$\hat{Y}=g^{-1}(\boldsymbol{\theta}^TX)$$

这样的模型称为广义线性模型（Generalized Linear Model，GLM），其中 $g(\cdot)$ 称为联系函数（Link Function）

显然，线性回归、对数线性回归、Logistic 回归是 GLM 的联系函数 $g(\cdot)$ 不同时的特例，可以总结为下表：

	联系函数	输出变量类型	使用场景
线性回归	$g(z)=z$	连续变量	身高、体重、房价等
对数线性回归	$g(z)=ln(z)$	计数变量	销售数量、车祸数量等
二元 Logistic 回归	$g(z)=ln\frac{P(z=1)}{1-P(z=1)}$	二分类变量	购买行为、投票行为等
多元 Logistic 回归	$g(z)=ln\frac{P(z=i)}{1-P(z=N)}$	多分类变量	评分等级、多分类模型等