【概述】
当分类数据超过两类时,即为多分类问题
对于多分类问题,可以将其进行拆解,转换为若干个独立的二元分类问题,进而借助分类学习方法来解决多分类问题
具体来说,先对问题进行进行拆分,然后为拆出的每个二分类任务训练一个分类器,在测试时,对这些分类器的预测结果进行集成,以获得最终的多分类结果
最常用的拆解策略有三种:
- 一对一(One vs One,OvO)
- 一对其余(One vs Rest,OvR)
- 多对多(Many vs Many,MvM)
【OvO】
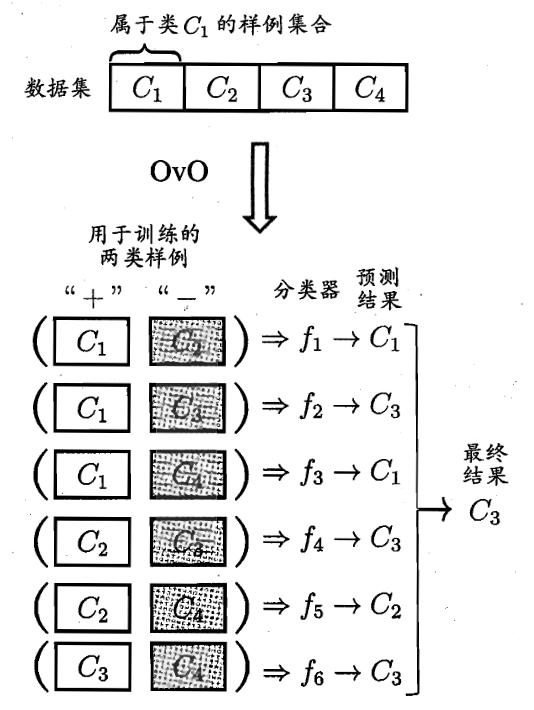
对于给定的训练数据集 $T=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$,第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值,即:$\mathbf{x_i} =(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$,输出 $y_i\in\mathcal{Y}= \{c_1,c_2,…,c_K\}$ 为实例的类别
OvO 策略会将这 $K$ 个类别两两配对,产生 $C(K,2)=\frac{K(K-1)}{2}$ 个二分类任务
之后,对划分好的 $C(K,2)$ 个任务分别使用分类器进行训练
在预测阶段,只需要将测试样本分别给在训练阶段训练好的 $C(K,2)$ 个分类器进行预测,再将这些预测结果进行投票统计,票数最多的即为最终的预测结果
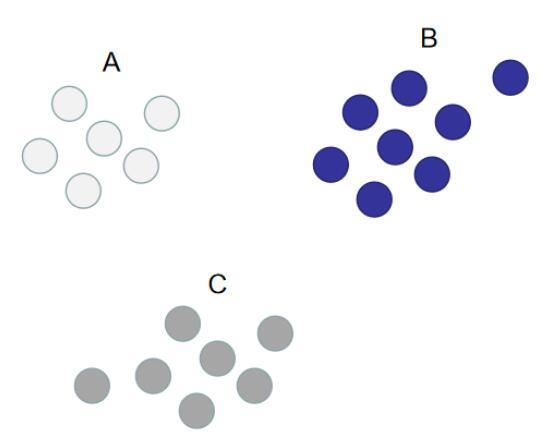
例如,下图中的训练集可分为 $A$、$B$、$C$ 三个类别
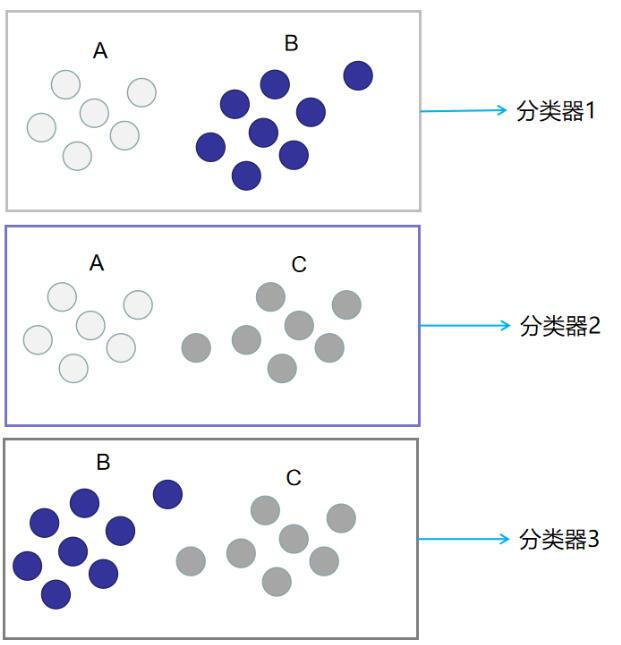
采用 OvO 策略后,$3$ 个类别两两配对,产生 $C(3,2)=\frac{3\cdot 2}{2}=3$ 个二分类任务,相应地,利用这三种划分就能得到 $3$ 个分类器
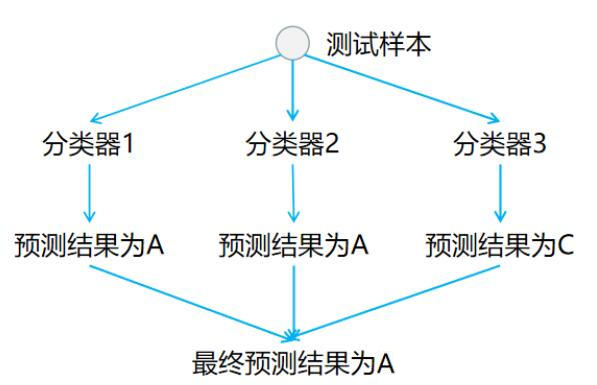
在预测阶段,只需要将测试样本分别给在训练阶段训练好的 $3$ 个分类器进行预测,最后利用投票法,票数最多的即为预测结果
【OvR】
对于给定的训练数据集 $T=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$,第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值,即:$\mathbf{x_i} =(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$,输出 $y_i\in\mathcal{Y}= \{c_1,c_2,…,c_K\}$ 为实例的类别
OvR 策略每次将一个类的样例作为正类,其他的所有类的样例作为反类,如此划分为 $K$ 个类别,产生 $K$ 个二分类任务,之后,对这 $K$ 个类别分别进行训练,训练出 $K$ 个分类器
在测试时,若仅有一个分类器预测为正类,则对应的类别标记为最终的分类结果;若有多个分类器预测为正类,则考虑各分类器的预测置信度,选择置信度最大的类别标记为最终的分类结果
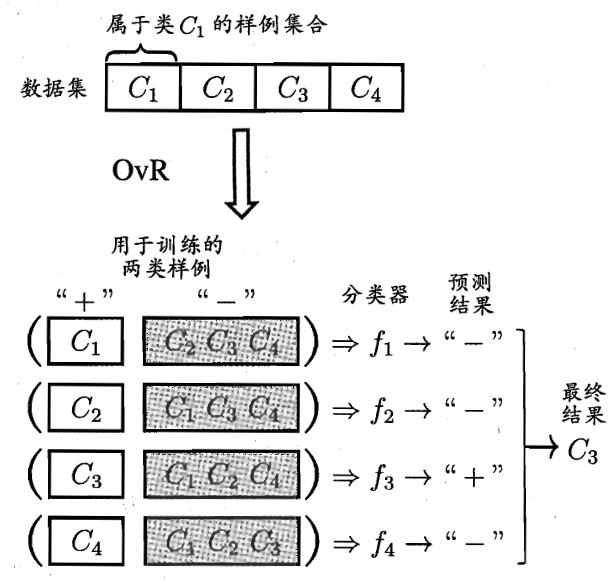
OvR 策略只需要训练 $K$ 个分类器,而 OvO 策略需要训练 $C(K,2)$ 个分类器,显然 OvO 策略的存储开销和时间开销要比 OvR 更大
但在实际使用时,OvO 策略并不需要像 OvR 策略一样使用全部样本进行训练,在类别很多时,使用 OvO 策略的时间开销反而要比 OvR 策略要小
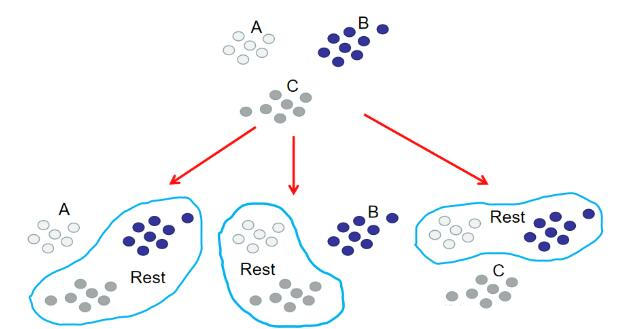
例如,下图中的训练集可分为 $A$、$B$、$C$ 三个类别

采用 OvR 策略后,$3$ 个类别分别作为正类,相应地剩余的两类别作为反类,产生 $3$ 个二分类任务
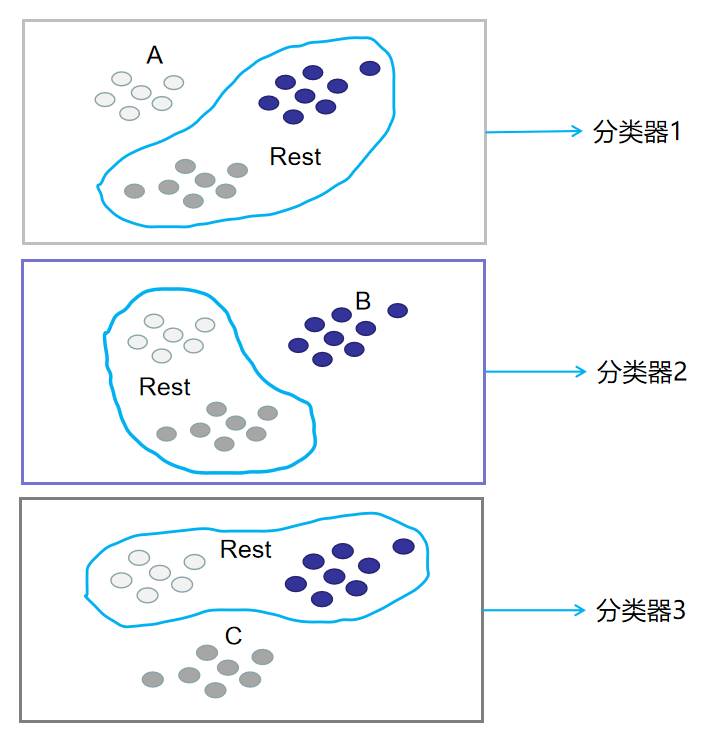
相应地,利用这三种划分就能得到 $3$ 个分类器
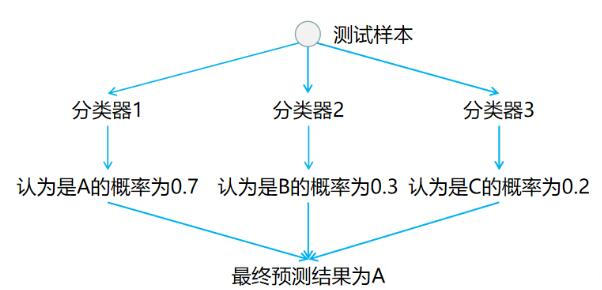
在预测阶段,只需要将测试样本分别给在训练阶段训练好的 $3$ 个分类器进行预测,最后对这些结果选择概率最高的类别作为最终结果
【MvM】
概述
对于给定的训练数据集 $T=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$,第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值,即:$\mathbf{x_i} =(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$,输出 $y_i\in\mathcal{Y}= \{c_1,c_2,…,c_K\}$ 为实例的类别
MvM 策略每次将若干类的样例作为正类,其他的所有类的样例作为反类,显然 OvO 策略与 OvR 策略是 MvM 策略的特例
MvM 策略的正、反类构造必须要有特殊的设计,不能随意选取,最常用的构造技术为:纠错输出码(Error Correcting Output Codes,ECOC)
ECOC
ECOC 是将编码思想引入到类别拆分中,并尽可能的在解码过程中具有容错性,其工作过程主要分两步:
- 编码:对 $K$ 个类别进行 $N$ 次划分,每次划分将一部分类别划分为正类,另一部分划分为反类,从而形成一个二分类训练集,这样一共产生 $N$ 个训练集,进而可训练出 $N$ 个分类器
- 解码:使用 $N$ 个分类器分别对测试样本进行预测,这些预测标记组成一个编码,将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为预测结果
类别划分通过编码矩阵(Coding Matrix)指定,其有多种形式,最常见的是利用海明码来编码的二元码和三元码
如下图,二元码将类别分为正类(-1)和负类(+1),后者在二元码的基础上又加了停用类(0),即分类器 $f_i$ 不使用该类样本
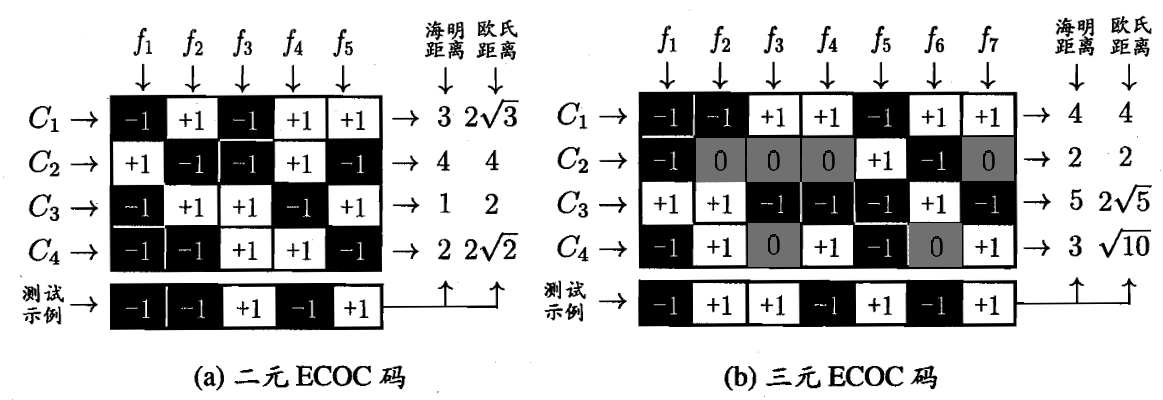
在解码阶段,各分类器的预测结果联合起来形成了测试实例的编码,该编码与各类所对应的编码进行比较,将距离最小的编码所对应的类作为预测结果,例如,在上图中的二元码中,基于欧氏距离,预测结果将为 $C_3$
在测试阶段,由于采取的是海明码,其对分类器的错误有一定的容忍和修正能力,在上图中,二元码中测试示例的正确编码是 $(-1,+1,+1,-1,+1)$,假设在预测时,分类器 $f_2$ 出错了,导致了出现错误编码 $(-1,-1,+1,-1,+1)$,但基于海明码与编码纠错理论,仍能产生正确的分类结果 $C_3$,这也是 ECOC 被称为纠错输出码的原因
一般来说,ECOC 编码越长,纠错能力越长,但编码越长意味着要训练分类器越多,计算、存储开销都会增大,同时,对于有限类别,可能的组合数目是有限的,码长在超过一定范围后,就失去了意义

