【梯度爆炸与梯度消失】
目前优化神经网络的方法基本都是基于反向传播的思想,即根据损失函数计算的误差通过反向传播的方式,逆向对网络权值进行更新
梯度消失和梯度爆炸是最常见的两个问题,它们会影响模型的收敛速度和性能
- 梯度爆炸(Gradient Explosion)是指在深度学习模型训练过程中,参数的梯度值变得非常大,导致模型参数更新过大,从而影响模型的收敛稳定性
- 梯度消失(Gradient Vanishing)是指在深度学习模型训练过程中,参数的梯度值变得非常小,接近于零,导致模型参数更新缓慢,从而影响模型的训练效果
【出现原因】
反向传播的不足
从网络结构的角度来说,假设存在一个 $L$ 层的全连接网络,每层的偏置 $b^l = 0$,不采用激活函数,那么对于输入 $X$,网络输出为:
- 当网络每层参数 $W^l>1$ 时,激活函数的值将以指数级递增
- 当网络每层参数 $W^l<1$ 时,激活函数的值将以指数级递减
反向传播算法是基于梯度下降的思想,以目标负梯度方向对参数进行调整,在计算梯度时,根据链式求导法则,最终求出的梯度更新将以指数级递增或递减,导致梯度爆炸或梯度消失
归结来说,神经网络不同层学习的速度差异很大,表现为网络中靠近输出层的层学习情况很好,靠近输入层的层学习很慢,可能训练很久,前基层的权值甚至与初值差不多,因此梯度爆炸和梯度消失的根本原因在于反向传播算法的不足
激活函数的选择
当选用的激活函数不合适时,梯度爆炸或梯度消失会更加明显
如下图,为 Sigmoid 函数和 Tanh 函数的导数,Sigmoid 函数的导数最大时只有 $0.25$,其余时刻远小于该值,因此若每层的激活函数都选择 Sigmoid 函数的话,经过链式求导后很容易导致梯度消失问题,同理,Tanh 函数的导数峰值为 $1$,其余时刻也远小于该值,经过链式求导后也容易导致梯度消失问题
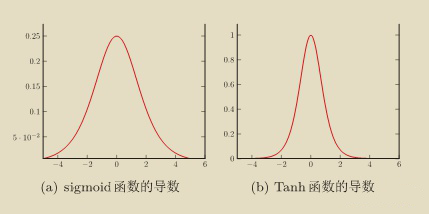
【解决方案】
激活函数的选择
在选用激活函数时,可选择 ReLUctance、Leak ReLU、ELU 等激活函数,解决梯度爆炸与梯度消失问题
如下图,为 ReLU 激活函数图像,其小于 $0$ 时梯度为 $0$,大于 $0$ 的时候梯度恒为 $1$,有效解决了梯度爆炸与梯度消失问题
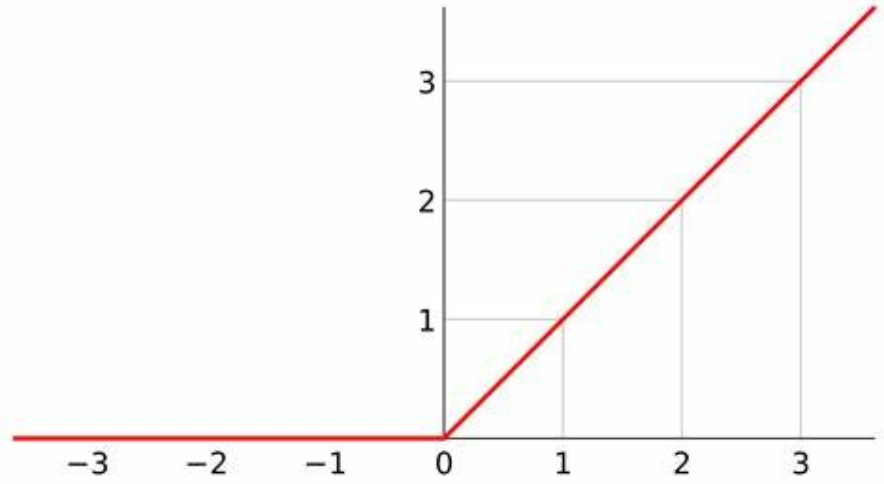
梯度截断
梯度截断(Gradient Clipping)又叫梯度剪切,其是防止梯度爆炸的一种方法,核心思想是设置一个阈值,在更新梯度时,如果梯度超过这个阈值,就将梯度强制限制在这个范围内
梯度剪切的方式有两种:
1.按值截断:在第 $t$ 次迭代时,梯度为 $g_t$,给定一个区间 $[a,b]$,若一个参数的梯度小于 $a$,就将梯度设为 $a$,若大于 $b$,就将梯度设为 $b$,即
2.按模截断:将梯度的模截断到一个给定的阈值 $b$,若 $||g_t||^2_2 \leq b$,保持 $g_t$ 不变,若 $||g_t||^2_2>b$,则令
按模截断常用于训练循环神经网络,可以有效避免梯度爆炸
标准化输入
对网络输入的特征进行标准化,将数据规整到统一区间,减少数据的发散程度,降低网络的学习难度,一定程度上缓解梯度爆炸与梯度消失问题
标准化的目的是使所有特征的平均值近似为 $0$,标准差近似为 $1$,其公式如下:
其中,$\mu$ 为平均值,$\sigma$ 为标准差
标准化前后的损失函数如下图所示
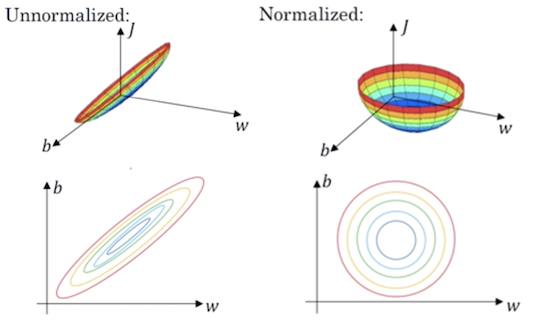
在经过标准化后,在梯度下降时无论从哪个位置开始迭代,都能以相对较少的迭代次数找到全局最优解,从而缓解梯度爆炸与梯度消失
批量归一化
批量归一化(Batch Normalization,BN)可以调整每一层的输入分布,有助于稳定训练过程,缓解梯度爆炸与梯度消失问题
关于批量归一化的详细介绍,见:批量归一化

