BP 神经网络与反向传播算法

【概述】

反向传播（Error Back Propagation，BP）算法，是迄今为止最成功的神经网络训练算法，其不仅可用于多层前馈神经网络中，还可用于其他神经网络，但通常说到 BP 神经网络时，一般是指用 BP 算法所训练的多层前馈神经网络，此外，在实际应用中，当使用神经网络建模时，大多使用 BP 算法进行训练

BP 算法是一种迭代学习算法，在迭代的每一轮中采用感知机学习算法对参数进行更新，其仍是基于梯度下降法，以目标的负梯度方向对参数进行调整

【符号假设】

对于给定的容量为 $N$ 的样本集 $D=\{(\mathbf{x}_1,\mathbf{y}_1),(\mathbf{x}_2,\mathbf{y}_2),…,(\mathbf{x}_N,\mathbf{y}_N)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $n$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(n)})\in \mathbb{R}^n$，输出 $\mathbf{y}_i$ 具有 $m$ 个特征值，即：$\mathbf{y}_i=(y_i^{(1)},y_i^{(2)},…,y_i^{(m)})\in\mathcal{Y}=\mathbb{R}^{m}$，也就是说，输入样本由 $n$ 个特征描述，输出为 $m$ 维实值向量

由于 BP 神经网络的参数很多，为便于讨论，给出如下符号假设：

1. 用 $n_l$ 表示网络层数
2. 用 $L_l$ 表示第 $l$ 层，$L_1$ 是输入层，$L_{n_l}$ 是输出层，其他为隐藏层
3. 用 $S_l$ 表示第 $l$ 层的神经元个数，输入层神经元个数 $S_1$ 为输入样本特征数 $n$，输出层神经元个数 $S_{n_l}$ 为输出特征个数 $m$
4. 用 $w_{ij}^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元与第 $l+1$ 层的第 $j$ 个神经元的连接权重
5. 用 $b_{i}^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元的偏置项（激活阈值）
6. 用 $z_{i}^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元的权重累计
7. 用 $a_i^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元的激活值（输出值）
8. 用 $\hat{y}$ 表示神经网络的输出值

如下图所示，给出了一个层数 $n_l=4$，各层神经元个数 $S_1=4,S_2=4,S_3=4,S_4=2$ 的多层前馈网络结构

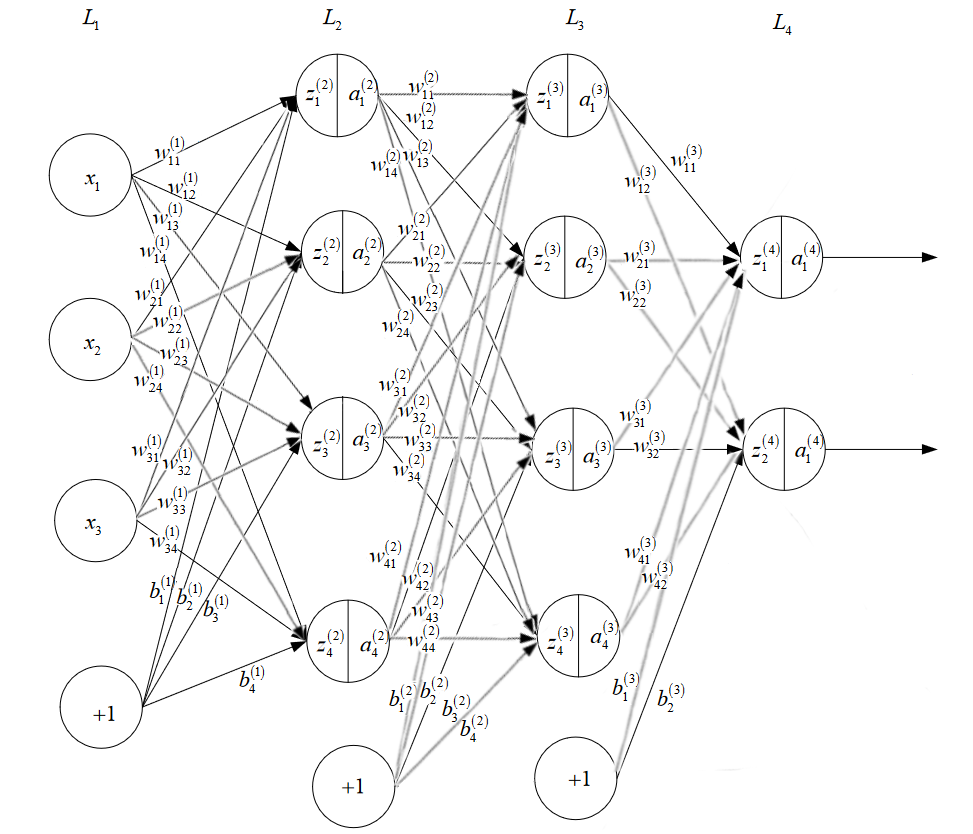
可以发现，网络中有 $(S_1+1)\times S_2 + (S_2+1)\times S_3+ (S_3+1)\times S_4 $ 个参数要确定，即：

• 输入层 $L_1$ 到隐藏层 $L_2$ 的 $S_1\times S_2$ 个权值（输入层 $L_1$ 第 $i$ 个神经元到隐藏层 $L_2$ 第 $j$ 个神经元：$w_{ij}^{[1]}$）
• 隐藏层 $L_2$ 到隐藏层 $L_3$ 的 $S_2\times S_3$ 个权值（隐藏层 $L_2$ 第 $i$ 个神经元到隐藏层 $L_3$ 第 $j$ 个神经元：$w_{ij}^{[2]}$）
• 隐藏层 $L_3$ 到输出层 $L_4$ 的 $S_3\times S_4$ 个权值（隐藏层 $L_3$ 第 $i$ 个神经元到输出层 $L_4$ 第 $j$ 个神经元：$w_{ij}^{[3]}$）
• 输入层 $L_1$ 神经元的偏置项（$S_2$ 个 $b_i^{[1]}$）
• 隐藏层 $L_2$ 神经元的偏置项（$S_3$ 个 $b_i^{[2]}$）
• 隐藏层 $L_3$ 神经元的偏置项（$S_4$ 个 $b_i^{[3]}$）

【前向传播】

前向传播（Forward Propagation，FP）就是将神经网络上一层的输出作为下一层的输入，并计算下一层的输出，直到运算到输出层为止

以具有两层隐藏层的总共层数 $n_l=4$ 的神经网络为例，各层的神经元个数分别为 $S_1=n,S_2,S_3,S_4=m$，对于输入样例 $\mathbf{x}=(x^{(1)},x^{(2)},…,x^{(n)})\in \mathbb{R}^n$，前向传播过程如下：

输入层 $L_1$：$l=1$，对于输入层的 $S_1=n$ 个神经元，有

$$a_i^{[1]}=x^{(i)},\quad i=1,2,\cdots,n$$

隐藏层 $L_2$：$l=2$，对于隐藏层的 $S_2$ 个神经元中的第 $j$ 个，权重累计为

$$\begin{gather*} z_j^{[2]} = \sum_{i=1}^{S_1=n} (w_{ij}^{[1]}a_i^{[1]})+b_j^{[1]} \end{gather*}$$

经过激活函数 $f(\cdot)$ 后，输出值为

$$\begin{align*} a_{j}^{[2]} &= f(z_{j}^{[2]}) \\ &= f(w_{1j}^{[1]}x^{(1)}+w_{2j}^{[1]}x^{(2)}+\cdots+w_{nj}^{[1]}x^{(n)}+b_j^{[1]}) \end{align*}$$

隐藏层 $L_3$：$l=3$，对于隐藏层的 $S_3$ 个神经元中的第 $j$ 个，权重累计为

$$\begin{gather*} z_j^{[3]} = \sum_{i=1}^{S_2} (w_{ij}^{[2]}a_i^{[2]})+b_j^{[2]} \end{gather*}$$

经过激活函数 $f(\cdot)$ 后，输出值为

$$\begin{align*} a_{j}^{[3]} &= f(z_{j}^{[3]}) \\ &= f(w_{1j}^{[2]}a_1^{[2]}+w_{2j}^{[2]}a_2^{[2]}+\cdots+w_{S_2 j}^{[2]}a_{S_2}^{[2]}+b_j^{[2]}) \end{align*}$$

输出层 $L_4$：$l=4$，对于输出层的 $S_4=m$ 个神经元中的第 $j$ 个，权重累计为

$$\begin{gather*} z_j^{[4]} = \sum_{i=1}^{S_3} (w_{ij}^{[3]}a_i^{[3]})+b_j^{[3]} \end{gather*}$$

经过激活函数 $f(\cdot)$ 后，输出值为

$$\begin{align*} a_{j}^{[4]} &= f(z_{j}^{[4]}) \\ &= f(w_{1j}^{[3]}a_1^{[3]}+w_{2j}^{[3]}a_2^{[3]}+\cdots+w_{S_3j}^{[3]}a_{S_3}^{[3]}+b_j^{[3]}) \end{align*}$$

最终神经网络的输出值为：

$$\begin{align*} \hat{\mathbf{y}} &= (a_1^{[4]},a_2^{[4]},\cdots,a_{m}^{[4]}) \\ &= (y^{(1)},y^{(2)},\cdots,y^{(m)}) \end{align*}$$

不失一般性，对于第 $L_l$ 层的第 $j$ 个神经元，前向传播过程可写为：

$$\begin{align*} z_j^{[l]} &= \sum_{i=1}^{S_{l-1}}(w_{ij}^{[l-1]}a_i^{[l-1]})+b_j^{[l-1]} \\ &= w_{1j}^{[l-1]}a_1^{[l-1]} +w_{2j}^{[l-1]}a_2^{[l-1]} + \cdots +w_{S_{l-1}j}^{[l-1]}a_{S_{l-1}}^{[l-1]} \\ a_j^{[l]} &= f(z_j^{[l]}) \end{align*}$$

对于 $N$ 个样本，将其矩阵化，有：

$$\begin{gather*} Z_{S_l\times N}^{[l]} = (W_{S_{l-1}\times S_l}^{[l-1]} )^T A_{S_{l-1}\times N}^{[l-1]} + \mathbf{b}_{S_l \times 1}^{[l-1]} \\ A_{S_l\times N}^{[l]} = f(Z_{S_l\times N}^{[l]}) \end{gather*}$$

其中，各符号含义如下：

• 输入矩阵 $A_{S_{l-1}\times N}^{[l-1]}$：$N$ 个样本在第 $l-1$ 层的输出矩阵
• 权重矩阵 $(W_{S_{l-1}\times S_l}^{[l-1]} )^T$：$N$ 个样本在第 $l-1$ 层与第 $l$ 层的连接权重
• 偏置向量 $\mathbf{b}_{S_l \times 1}^{[l-1]}$：$N$ 个样本在第 $l-1$ 层的偏置向量
• 权重累计矩阵 $Z_{S_l\times N}^{[l]}$：$N$ 个样本在第 $l$ 层的权重累计矩阵
• 输出矩阵 $A_{S_l\times N}^{[l]}$：$N$ 个样本在第 $l$ 层的输出矩阵

【损失函数】

对于给定的容量为 $N$ 的样本集 $D=\{(\mathbf{x}_1,\mathbf{y}_1),(\mathbf{x}_2,\mathbf{y}_2),…,(\mathbf{x}_N,\mathbf{y}_N)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $n$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(n)})\in \mathbb{R}^n$，输出 $\mathbf{y}_i$ 具有 $m$ 个特征值，即：$\mathbf{y}_i=(y_i^{(1)},y_i^{(2)},…,y_i^{(m)})\in\mathcal{Y}=\mathbb{R}^{m}$

假设存在一具有 $n_l$ 层的神经网络，各层神经元个数为 $S_1=n,S_2,S_3,\cdots,S_{n_l}=m$，对于样本集中的第 $k$ 个样本 $(\mathbf{x}_k,\mathbf{y}_k)$，其通过神经网络的输出为 $\hat{\mathbf{y}}_k=(\hat{y_k}^{(1)},\hat{y_k}^{(2)},…,\hat{y_k}^{(m)})$，那么平方损失函数为：

$$E_{k}= (\hat{\mathbf{y}}_k-\mathbf{y}_k)^2$$

为便于求导，对 $E_k$ 整体乘以 $\frac{1}{2}$，此时得到的函数为第 $k$ 个样本的损失函数，即：

$$E_k= \frac{1}{2}(\hat{\mathbf{y}}_k-\mathbf{y}_k)^2$$

进一步，对于容量为 $N$ 的样本集，其损失函数为：

$$\begin{align*} J(w,b) &= \frac{1}{N}\sum_{k=1}^N E_k\\ &= \frac{1}{2N}\sum_{k=1}^N \sum_{j=1}^m(\hat{y}_k^{(j)}-y_k^{(j)})^2 \\ \end{align*}$$

可以看出，损失函数 $J(w,b)$ 是惯有所有权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$ 的方程，要通过求损失函数最小来得到最佳的权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$，可以采用梯度下降法逐步下降迭代得到，即：

$$\begin{align*} w_{ij}^{[l]} = w_{ij}^{[l]} - \alpha \frac{\partial}{\partial w_{ij}^{[l]}} J(w,b) \\ b_{i}^{[l]} = b_{i}^{[l]} - \alpha \frac{\partial}{\partial b_{i}^{[l]}} J(w,b) \end{align*}$$

那么，只需要求出各权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$ 的偏导，即可对神经网络进行优化，但直接对上式进行计算十分困难，为此有了反向传播算法，从后向前求导进行更新

【反向传播】

反向传播（Backward Propagation，BP）是一种计算梯度的方法，原则上其可以计算任何函数的导数

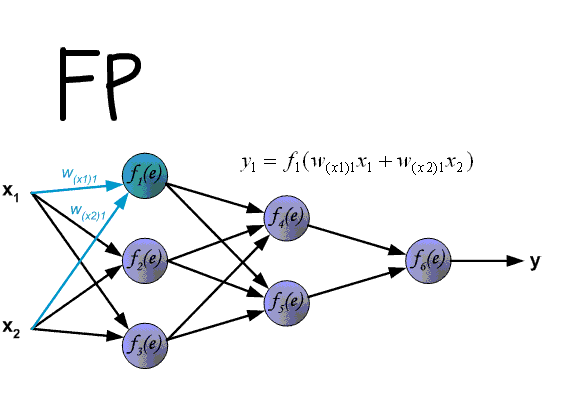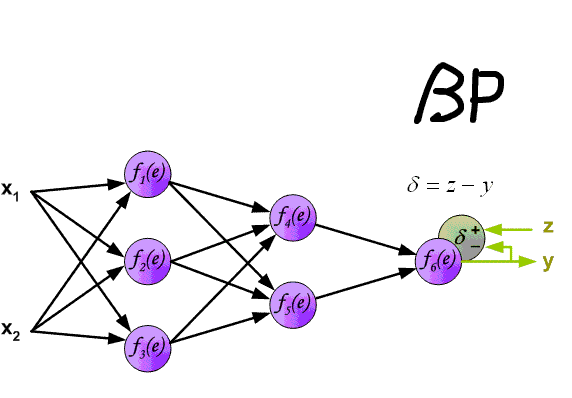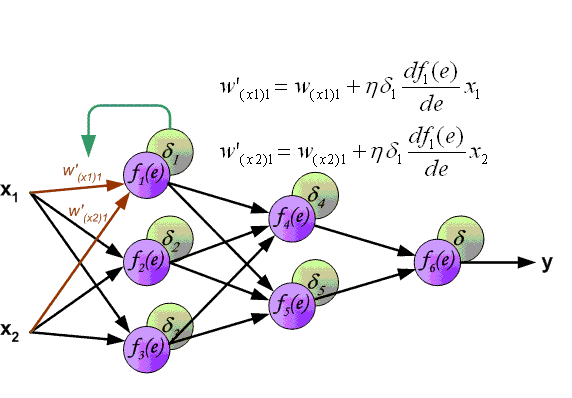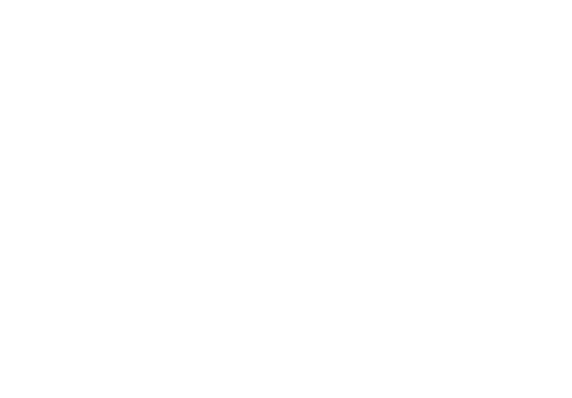
在前向传播完成后，需要使用梯度下降法来对各权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$ 进行更新，但由于直接对神经网络的梯度下降公式求导十分困难，因此有了 BP 算法，其可以简单的理解为利用链式求导法则，从后向前逐层计算损失函数 $J(w,b)$ 对各权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$ 的梯度，然后进行更新，这也是算法被称为反向传播的原因

通过 BP 算法，最终得到的梯度下降方程为：

$$\begin{gather*} w_{ij}^{[l]} = w_{ij}^{[l]}-\alpha \cdot \delta_j^{[l+1]} a_i^{[l]} \\ b_{i}^{[l]} = b_{i}^{[l]}-\alpha \cdot \delta_i^{[l+1]} \\ \end{gather*}$$

当 $l=1$ 时，$a_i^{[1]}$ 即为输入 $x^{(i)}$

其中，$\alpha$ 为学习率，$\delta_{j}^{[l]}$ 为第 $L_l$ 层第 $j$ 个神经元的误差，有：

$$\begin{gather*} \delta_{j}^{[l]} = \sum\limits_{k=1}^{S_{l+1}} \bigg[ \delta_k^{[l+1]} \cdot w_{jk}^{[l]} \cdot f'(z_j^{[l]}) \bigg], & l=n_l-1,n_l-2,\cdots,3,2\\ \delta_j^{[n_l]}=\Big[ f(z_j^{[n_l]})-y^{(j)} \Big]\cdot f'(z_j^{[n_l]}), & l=n_l \end{gather*}$$

关于具体的推导过程，见：附：详细推导

【算法流程】

输入：容量为 $N$ 的样本集 $D=\{(\mathbf{x}_1,\mathbf{y}_1),(\mathbf{x}_2,\mathbf{y}_2),…,(\mathbf{x}_N,\mathbf{y}_N)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $n$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(n)})\in \mathbb{R}^n$，输出 $\mathbf{y}_i$ 具有 $m$ 个特征值，即：$\mathbf{y}_i=(y_i^{(1)},y_i^{(2)},…,y_i^{(m)})\in\mathcal{Y}=\mathbb{R}^{m}$，学习率 $0<\alpha\leq1$，迭代轮次 $\text{epoch}$，损失函数阈值 $\text{threshold}$

输出：连接权与阈值确定的多层前馈神经网络

算法步骤：

Step1：在 $(0,1)$ 范围内，随机初始化网络中所有的连接权重与偏置项

Step2：对于训练集中的每个样本 $(\mathbf{x}_k,\mathbf{y}_k)$，执行以下步骤：

1.根据网络结构，进行前向传播，计算网络输出 $\hat{\mathbf{y}}_k=(\hat{y_k}^{(1)},\hat{y_k}^{(2)},…,\hat{y_k}^{(m)})$

2.根据网络结构，进行反向传播，更新参数

1）对 $L_{n_l}$ 层，计算误差 $\boldsymbol{\delta}^{[n_l]}$

$$\delta_j^{[n_l]}=\Big[ f(z_j^{[n_l]})-y^{(j)} \Big]\cdot f'(z_j^{[n_l]})$$

2）对 $L_l,l=n_l-1,n_l-2,\cdots,3,2$ 层，计算误差 $\boldsymbol{\delta}^{[l]}$

$$\delta_{j}^{[l]} = \sum\limits_{k=1}^{S_{l+1}} \bigg[ \delta_k^{[l+1]} \cdot w_{jk}^{[l]} \cdot f'(z_j^{[l]}) \bigg]$$

3）对连接权重与偏置进行更新

$$\begin{gather*} w_{ij}^{[l]} = w_{ij}^{[l]}-\alpha \cdot \delta_j^{[l+1]} a_i^{[l]} \\ b_{i}^{[l]} = b_{i}^{[l]}-\alpha \cdot \delta_i^{[l+1]} \\ \end{gather*}$$

当 $l=1$ 时，$a_i^{[1]}$ 即为输入 $x^{(i)}$

Step3：重复 Step2，直到训练集的损失函数 $J(w,b)$ 达到要求的值，或完成迭代轮数

---

通过上述算法流程可以发现，对于每个训练集中的每个训练样本，BP 算法先将输入提供给输入层单元，然后逐层将信号前传，直到产生输出层结果（步骤 Step2.1）

之后，再计算输出层的误差（步骤 Step2.2），将误差逆向传播至隐藏层（步骤 Step2.3），根据隐藏层神经元的误差对连接权和阈值进行调整（步骤 Step2.4）

下图给出了一个多层前馈神经网络的 FP 与 BP 的完整过程

【实现】

采用向量化编程，实现下图所示的单隐藏层二分类神经网络，损失函数采用交叉熵损失函数，网络结构为：

• 输入层 $L_1$：两个神经元
• 隐藏层 $L_2$：四个神经元，采用 tanh 激活函数
• 输出层 $L_3$：一个神经元，采用 sigmoid 激活函数

实现步骤为：

1. 定义网络结构
2. 初始化连接权重与偏置
3. 循环以下步骤，直到完成迭代轮数
   1. 前向传播
   2. 计算损失
   3. 反向传播获得梯度
   4. 梯度更新

代码如下：

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets
import sklearn.linear_model
from load_dataset import load_planar_dataset

''' 
sigmoid损失函数
''' 
def sigmoid(x):
    s = 1/(1+np.exp(-x))
    return s
    
''' 
定义网络结构
输入：
 - X: n × N
 - Y: m × N
输入层L1维度：n_x = n
隐藏层L2维度：n_h = 4
输出层L3维度：n_y = m
'''
def layer_sizes(X, Y):
    # 输入层大小
    n_x = X.shape[0]
    # 隐层大小
    n_h = 4
    # 输出层大小
    n_y = Y.shape[0]
    return (n_x, n_h, n_y)

'''
初始化模型参数
L1到L2参数维度：
 - W1：n_h × n_x
 - b1：n_h × 1
L1到L2参数维度：
 - W2：n_y × n_h
 - b2：n_y × 1
'''
def initialize_parameters(n_x, n_h, n_y):
    np.random.seed(2)
    
    # L1层到L2层的连接权重向量w1和偏置向量b1
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    
    # L2层到L3层的连接权重向量w2和偏置向量b2
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    
    # 检测维度是否符合要求
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

'''
前向传播
L1到L2层：
 - Z1 = W1X + b1, 维度：n_h × N = (n_h × n_x) · (n_x × N) + (n_h × 1)
 - A1 = tanh(Z1), 维度：n_h × N
L2到L3层：
 - Z2 = W2A1 + b2, 维度：n_y × N = (n_y × n_h) · (n_h × N) + (n_y × 1)
 - A2 = tanh(Z2), 维度：n_y × N
'''
def forward_propagation(X, parameters):
    # 获取参数
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    
    # L1层到L2层
    Z1 = np.matmul(W1, X) + b1
    A1 = np.tanh(Z1)
    
    # L2层到L3层
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)
    
    # 判断维度是否符合要求
    assert(A2.shape == (1, X.shape[1]))
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

'''
计算损失函数，采用交叉熵损失函数
'''
def compute_cost(A2, Y, parameters):
    # 样本数量
    m = Y.shape[1]
    
    logpro = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), (np.log(1 - A2)))
    cost = - 1 / m * np.sum(logpro)
    cost = np.squeeze(cost)
    
    assert(isinstance(cost, float))
    
    return cost

'''
反向传播计算梯度
parameters：参数
cache：每层前向传播的计算结果
'''
def backward_propagation(parameters, cache, X, Y):
    # 样本数量
    m = X.shape[1]
    
    # 获取参数
    W1 = parameters['W1']
    W2 = parameters['W2']
    
    # 获取前向传播的结果
    A1 = cache['A1']
    A2 = cache['A2']
    
    # 反向传播计算梯度
    # 最后一层
    dZ2 = A2 - Y
    dW2 = 1/m * np.dot(dZ2, A1.T)
    db2 = 1/m * np.sum(dZ2, axis=1, keepdims=True)
    # 隐藏层
    dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
    dW1 = 1/m * np.dot(dZ1, X.T)
    db1 = 1/m * np.sum(dZ1, axis=1, keepdims=True)

    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

"""
更新梯度
"""
def update_parameters(parameters, grads, learning_rate = 0.005):
    # 获取参数
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    
    # 获取梯度
    dW1 = grads['dW1']
    db1 = grads['db1']
    dW2 = grads['dW2']
    db2 = grads['db2']
    
    # 更新参数
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

'''
建立神经网络模型
'''
def nn_model(X, Y, num_iterations = 10000, print_cost=False):
    np.random.seed(3)
    
    # 获取网络的层大小
    n_x, n_h, n_y = layer_sizes(X, Y)
    
    # 初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    
    # 循环直到完成迭代轮次
    for i in range(0, num_iterations):
        # 前向传播
        A2, cache = forward_propagation(X, parameters)
        
        # 计算损失
        cost = compute_cost(A2, Y, parameters)
        
        # 反向传播计算梯度
        grads = backward_propagation(parameters, cache, X, Y)
        
        # 利用梯度更新参数
        parameters = update_parameters(parameters, grads)
        
        # 每迭代1000次打印一次损失函数
        if i % 1000 == 0:
            print ("迭代次数 %i: %f" %(i, cost))

    return parameters

'''
预测
'''
def predict(parameters, X): 
    # 前向传播获取网络输出
    A2, cache = forward_propagation(X, parameters)
    
    # 根据概率值判断类别
    predictions = np.array( [1 if x >0.5 else 0 for x in A2.reshape(-1,1)] ).reshape(A2.shape)
    
    return predictions

if __name__ == "__main__":
    # 获取数据集
    X, Y = load_planar_dataset()
    print ('数据集特征值的形状:', X.shape)
    print ('数据集目标值的:', Y.shape)
    print ('样本数:', X.shape[1])
    
    # 建立模型获取网络参数
    parameters = nn_model(X, Y, num_iterations = 10000)

    # 预测
    predictions = predict(parameters, X)
    
    # 准确率
    print ('准确率: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')

【附：详细推导】

问题转化

对于一个层数为 $n_l$ 的神经网络，各层神经元个数为 $S_1=n,S_2,S_3,\cdots,S_{n_l}=m$，对损失函数求第 $l$ 层的各权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$ 的偏导，有：

$$\begin{gather*} \frac{\partial}{\partial w_{ij}^{[l]}} J(w,b) = \frac{1}{N} \sum_{k=1}^N \frac{\partial}{\partial w_{ij}^{[l]}}E_k \\ \frac{\partial}{\partial b_{i}^{[l]}} J(w,b) = \frac{1}{N} \sum_{k=1}^N \frac{\partial}{\partial b_{i}^{[l]}}E_k \end{gather*}$$

此时，问题转化为求每个样本的损失函数 $E_k$ 关于各权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$ 的偏导

$L_{n_l-1}$ 层的偏导

对任一样本 $(\mathbf{x},\mathbf{y})$，有：

$$E= \frac{1}{2}(\hat{\mathbf{y}}-\mathbf{y})^2$$

$\hat{\mathbf{y}}$ 是输出层 $L_{n_l}$ 的输出，其是关于 $L_{n_l-1}$ 层的 $w$ 和 $b$ 的函数，由此，考虑从 $L_{n_l-1}$ 层开始对损失函数求偏导，看能否找到规律

即对损失函数 $J(w,b)$，求第 $L_{n_l-1}$ 层关于各权重 $w_{ij}^{[n_l-1]}$ 的偏导，即：

$$\begin{align*} \frac{\partial}{\partial w_{ij}^{[n_l-1]}} J(w,b) &= \frac{\partial}{\partial w_{ij}^{[n_l-1]}} \frac{1}{2} (\hat{\mathbf{y}}-\mathbf{y})^2 \\ &= \frac{\partial}{\partial w_{ij}^{[n_l-1]}} \frac{1}{2} (\mathbf{a}^{[n_l]}-\mathbf{y})^2 \\ &= \frac{\partial}{\partial w_{ij}^{[n_l-1]}} \frac{1}{2} \sum_{k=1}^{S_{nl}}(a_k^{[n_l]}-y^{(k)})^2 \\ &= \frac{\partial}{\partial w_{ij}^{[n_l-1]}} \frac{1}{2} \sum_{k=1}^{S_{nl}} \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2 \\ \end{align*}$$

根据前向传播，输出层 $L_{n_l}$ 的第 $k$ 个神经元的权重累计 $z_k^{[n_l]}$ 为：

$$z_k^{[n_l]} = \sum_{p=1}^{S_{n_l-1}} w_{pk}^{[n_l-1]}a_p^{[n_l-1]}+b_k^{[n_l-1]}$$

那么，根据链式求导法则，有：

$$\begin{align*} \frac{\partial}{\partial w_{ij}^{[n_l-1]}} J(w,b) &= \frac{\partial}{\partial w_{ij}^{[n_l-1]}} \frac{1}{2} \sum_{k=1}^{S_{nl}} \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2 \\ &= \frac{\partial}{\partial z_j^{[n_l]}} \bigg[ \frac{1}{2} \sum_{k=1}^{S_{n_l}} \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2 \bigg] \cdot \frac{\partial z_j^{[n_l]}}{\partial w_{ij}^{[n_l-1]}} \\ &= \Big[ f(z_j^{[n_l]})-y^{(j)} \Big] \cdot f'(z_j^{[n_l]}) \cdot \frac{\partial z_j^{[n_l]}}{\partial w_{ij}^{[n_l-1]}} \\ &= \Big[ f(z_j^{[n_l]})-y^{(j)} \Big] \cdot f'(z_j^{[n_l]}) \cdot a_i^{[n_l-1]} \end{align*}$$

此时，第 $L_{n_l}$ 层第 $j$ 个的神经元差为：

$$\delta_j^{[n_l]}=\Big[ f(z_j^{[n_l]})-y^{(j)} \Big]\cdot f'(z_j^{[n_l]})$$

对于最后的输出层来说，由于样本输出 $y^{(j)}$、由前向传播得来的神经元输出 $f(z_j^{[n_l]})$ 以及其导数是确定的，因此误差 $\delta_j^{[n_l]}$ 也能确定下来

$L_{n_l-2}$ 层的偏导

根据从 $L_{n_l-1}$ 层确定的误差 $\delta_j^{[n_l]}$，向前推第 $L_{n_l-2}$ 层对损失函数关于各权重的偏导，即对损失函数 $J(w,b)$，求第 $L_{n_l-2}$ 层关于各权重 $w_{ij}^{[n_l-2]}$ 的偏导，即：

$$\begin{align*} \frac{\partial}{\partial w_{ij}^{[n_l-2]}} J(w,b) &= \frac{\partial}{\partial w_{ij}^{[n_l-2]}} \frac{1}{2} (\hat{\mathbf{y}}-\mathbf{y})^2 \\ &= \frac{\partial}{\partial w_{ij}^{[n_l-2]}} \frac{1}{2} (\mathbf{a}^{[n_l]}-\mathbf{y})^2 \\ &= \frac{\partial}{\partial w_{ij}^{[n_l-2]}} \frac{1}{2} \sum_{k=1}^{S_{nl}} \Big[ a_k^{[n_l]}-y^{(k)} \Big]^2 \\ &= \frac{\partial}{\partial w_{ij}^{[n_l-2]}} \frac{1}{2} \sum_{k=1}^{S_{nl}} \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2 \\ \end{align*}$$

根据前向传播，隐藏层 $L_{n_l-1}$ 的第 $k$ 个神经元的权重累计 $z_k^{[n_l-1]}$ 为：

$$z_k^{[n_l-1]} = \sum_{p=1}^{S_{n_l-2}} w_{pk}^{[n_l-2]}a_p^{[n_l-2]}+b_k^{[n_l-2]}$$

那么，根据链式求导法则，有：

$$\begin{align*} \frac{\partial}{\partial w_{ij}^{[n_l-2]}} J(w,b) &= \frac{\partial}{\partial w_{ij}^{[n_l-2]}} \frac{1}{2} \sum_{k=1}^{S_{nl}} \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2 \\ &= \frac{\partial}{\partial z_j^{[n_l-1]}} \bigg[ \frac{1}{2} \sum_{k=1}^{S_{n_l}} \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2 \bigg] \cdot \frac{\partial z_j^{[n_l-1]}}{\partial w_{ij}^{[n_l-2]}} \\ &= \sum_{k=1}^{S_{n_l}} \bigg[ \frac{1}{2} \frac{\partial \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2 }{\partial z_{j}^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}} \bigg[\frac{1}{2}\frac{\partial \Big[ f(z_k^{[n_l]})-y^{(k)} \Big]^2}{\partial f(z_k^{[n_l]})} \cdot \frac{\partial f(z_k^{[n_l]})}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}}\bigg[ \Big[ f(z_k^{[n_l]})-y^{(k)} \Big] \cdot \frac{\partial f(z_k^{[n_l]})}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \end{align*}$$

对于输出层 $L_{n_l}$ 的第 $k$ 个神经元，其权重累计 $z_k^{[n_l]}$ 受到前一层 $L_{n_l-1}$ 的所有神经元的权重累计 $z_i^{[n_l-1]}$ 的影响，故有：

$$\begin{align*} \frac{\partial}{\partial w_{ij}^{[n_l-2]}} J(w,b) &= \sum_{k=1}^{S_{n_l}}\bigg[ \Big[ f(z_k^{[n_l]})-y^{(k)} \Big] \cdot \frac{\partial f(z_k^{[n_l]})}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}}\bigg[ \Big[ f(z_k^{[n_l]})-y^{(k)} \Big] \cdot \frac{\partial f(z_k^{[n_l]})}{\partial z_k^{[n_l]}} \cdot \frac{\partial z_k^{[n_l]}}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}}\bigg[ \Big[ f(z_k^{[n_l]})-y^{(k)} \Big] \cdot f'(z_k^{[n_l]}) \cdot \frac{\partial z_k^{[n_l]}}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ \end{align*}$$

由于第 $L_{n_l}$ 层第 $j$ 个神经元的误差为 $\delta_j^{[n_l]}=\Big[ f(z_j^{[n_l]})-y^{(j)} \Big]\cdot f’(z_j^{[n_l]})$，故有：

$$\begin{align*} \frac{\partial}{\partial w_{ij}^{[n_l-2]}} J(w,b) &= \sum_{k=1}^{S_{n_l}}\bigg[ \Big[ f(z_k^{[n_l]})-y^{(k)} \Big] \cdot f'(z_k^{[n_l]}) \cdot \frac{\partial z_k^{[n_l]}}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}}\bigg[ \delta_k^{[n_l]} \cdot \frac{\partial z_k^{[n_l]}}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ \end{align*}$$

进一步，根据 $z_k^{[n_l]} = \sum\limits_{p=1}^{S_{n_l-1}} w_{pk}^{[n_l-1]}a_p^{[n_l-1]}+b_k^{[n_l-1]}$，有：

$$\begin{align*} \frac{\partial}{\partial w_{ij}^{[n_l-2]}} J(w,b) &= \sum_{k=1}^{S_{n_l}}\bigg[ \delta_k^{[n_l]} \cdot \frac{\partial z_k^{[n_l]}}{\partial z_j^{[n_l-1]}} \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}}\bigg[ \delta_k^{[n_l]} \cdot \frac{\partial}{\partial z_j^{[n_l-1]}} \Big[\sum_{i=1}^{S_{n_l-1}} w_{ij}^{[n_l-1]}a_i^{[n_l-1]}+b_j^{[n_l-1]}\Big] \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}}\bigg[ \delta_k^{[n_l]} \cdot \frac{\partial}{\partial z_j^{[n_l-1]}} \Big[\sum_{i=1}^{S_{n_l-1}} w_{ij}^{[n_l-1]}f(z_i^{[n_l-1]})+b_j^{[n_l-1]}\Big] \bigg] \cdot a_i^{[n_l-2]} \\ &= \sum_{k=1}^{S_{n_l}}\bigg[ \delta_k^{[n_l]} \cdot w_{jk}^{[n_l-1]} \cdot f'(z_j^{[n_l-1]})\bigg] \cdot a_i^{[n_l-2]} \\ \end{align*}$$

其中，$w_{jk}^{[n_l-1]}$ 是隐藏层 $L_{n_l-1}$ 第 $j$ 个神经元与输出层 $L_{n_l}$ 第 $k$ 个神经元的连接权重

综上，第 $L_{n_l-2}$ 层各权重 $w_{ij}^{[n_l-2]}$ 的偏导为：

$$\frac{\partial}{\partial w_{ij}^{[n_l-2]}} J(w,b) = \sum_{k=1}^{S_{n_l}}\bigg[ \delta_k^{[n_l]} \cdot w_{jk}^{[n_l-1]} \cdot f'(z_j^{[n_l-1]})\bigg] \cdot a_i^{[n_l-2]}$$

此时，第 $L_{n_l-1}$ 层第 $j$ 个神经元的误差为：

$$\delta_j^{[n_l-1]}=\sum_{k=1}^{S_{n_l}}\bigg[ \delta_k^{[n_l]} \cdot w_{jk}^{[n_l-1]} \cdot f'(z_j^{[n_l-1]})\bigg]$$

此时，由于第 $L_{n_l}$ 层的误差 $\delta_k^{[n_l]}$ 、由前向传播得来的第 $L_{n_l-1}$ 层第 $j$ 个神经元的连接权重 $w_{jk}^{[n_l-1]}$ 以及神经元输出 $f(z_j^{[n_l-1]})$ 的导数是确定的，因此误差 $\delta_j^{[n_l-1]}$ 也能确定下来

梯度下降方程

根据第 $L_{n_l-1}$ 层、第 $L_{n_l-2}$ 层连接权重的推导，以此类推，可以得出第 $L_l$ 层的误差，即：

$$\delta_{j}^{[l]} = \sum_{k=1}^{S_{l+1}} \bigg[ \delta_k^{[l+1]} \cdot w_{jk}^{[l]} \cdot f'(z_j^{[l]}) \bigg]$$

于是可得出，对于第 $L_l$ 层，损失函数关于各权重 $w_{ij}^{[l]}$ 和偏置 $b_i^{[l]}$ 的偏导为：

$$\begin{gather*} \frac{\partial}{\partial w_{ij}^{[l]}} J(w,b) = \delta_j^{[l+1]} a_{i}^{[l]} \\ \frac{\partial}{\partial b_{i}^{[l]}} J(w,b) = \delta_i^{[l+1]} \\ \end{gather*}$$

故最终的梯度下降方程为：

$$\begin{gather*} w_{ij}^{[l]} = w_{ij}^{[l]}-\alpha \cdot \delta_j^{[l+1]} a_i^{[l]} \\ b_{i}^{[l]} = b_{i}^{[l]}-\alpha \cdot \delta_i^{[l+1]} \\ \end{gather*}$$

其中，$\alpha$ 为学习率，$\delta_{j}^{[l]} = \sum\limits_{k=1}^{S_{l+1}} \bigg[ \delta_k^{[l+1]} \cdot w_{jk}^{[l]} \cdot f’(z_j^{[l]}) \bigg]$ 为第 $L_l$ 层第 $j$ 个神经元的误差

点击返回