【概述】
2020 年 6 月,Jonathan Ho 等学者在《Denoising Diffusion Probabilistic Models》中对之前的扩散概率模型进行了简化,并通过变分推断,将后验问题转为优化问题进行建模,提出了经典的去噪扩散概率模型(Denoising Diffusion Probabilistic Model,DDPM),将扩散概率模型的思想用于图像生成,目前所说的扩散模型,大多是基于该模型进行改进
简单来说,DDPM 包含两个过程:
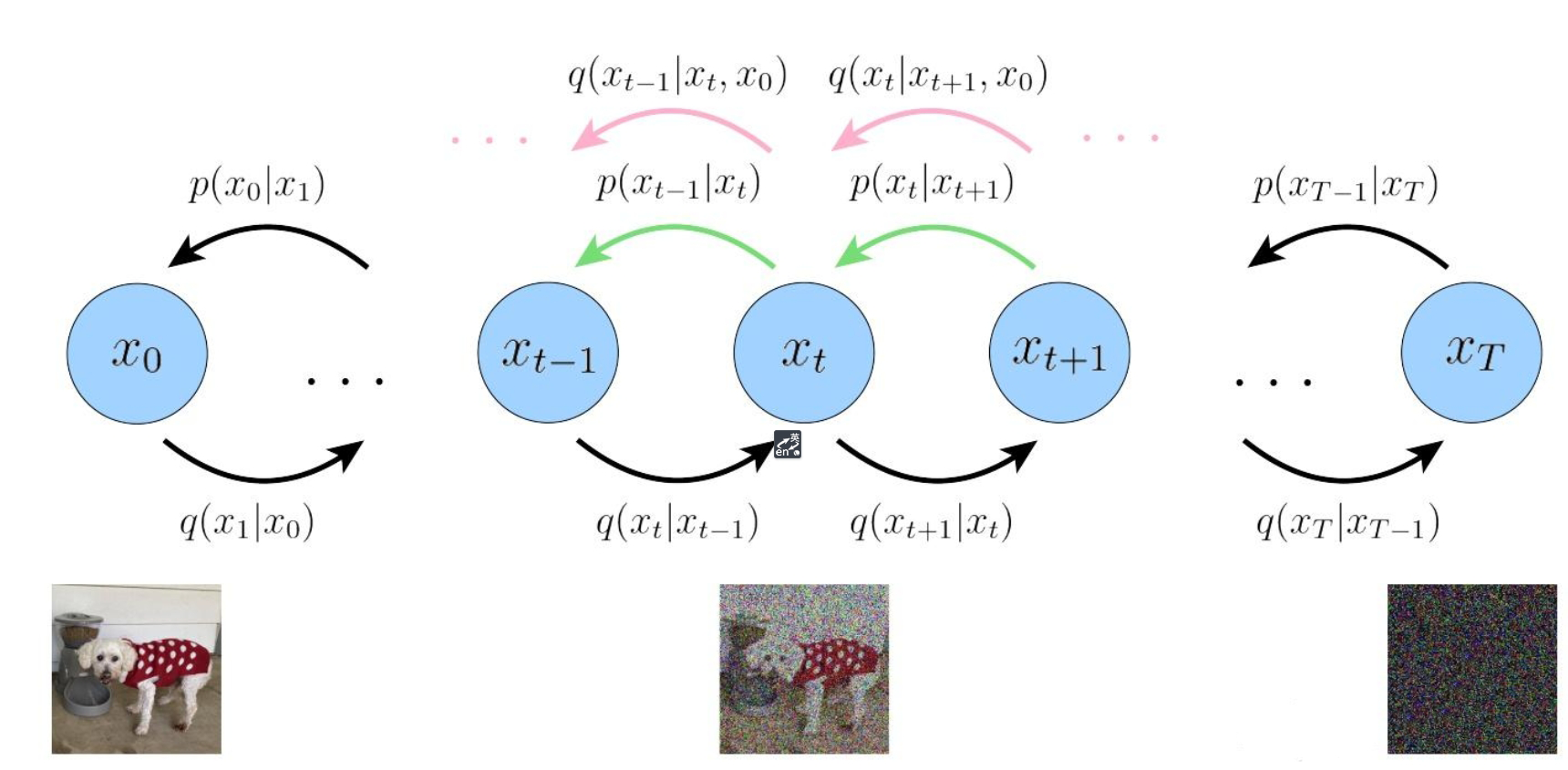
- 前向扩散过程 $\mathbf{x}_{0}\rightarrow \mathbf{x}_{T}$:逐步加噪的前向过程,该过程从原始图片逐步添加高斯噪声,直到变为随机噪声
- 反向生成过程 $\mathbf{x}_T\rightarrow \mathbf{x}_0$:逐步去噪的反向过程,该过程将随机噪声逐步去除噪声,直到还原为一张图片

其采用一个 U-Net 结构的 Autoencoder 来对 $t$ 时刻的噪声进行预测,在训练过程中,模型会逐步学习如何从噪声中生成数据,并逐渐引入结构和模式信息
【引入】
在 扩散概率模型 中,详细介绍了扩散概率模型,其是 DDPM 的起源模型,具体来说,扩散概率模型是形如
的潜变量模型,其中,$\mathbf{x}_1,\cdots,\mathbf{x}_T$ 是与数据 $\mathbf{x}_0\sim q(\mathbf{x}_0)$ 相同维数的潜变量
前向过程
反向过程
【基本过程】
前向扩散过程
对于前向扩散过程,其是一个加噪过程,从满足初始分布 $ q(\mathbf{x}_0)$ 的原始数据 $\mathbf{x}_0$ 出发,产生一系列带有噪声的图片,并利用前一时刻的图片去预测下一时刻的图片
对于扩散概率模型中的前向过程:
$\{\beta_t\}_{t=1}^T,\beta_t\in (0,1)$ 是每一步扩散采用的方差,通常随着 $t$ 的增加 $\beta_t$ 而增大,即满足 $\beta_1<\beta_2<\cdots<\beta_T$,当扩散步数 $T$ 足够大,那么最终得到的 $\mathbf{x}_T$ 就完全丢失了原始数据,变成一个随机噪声
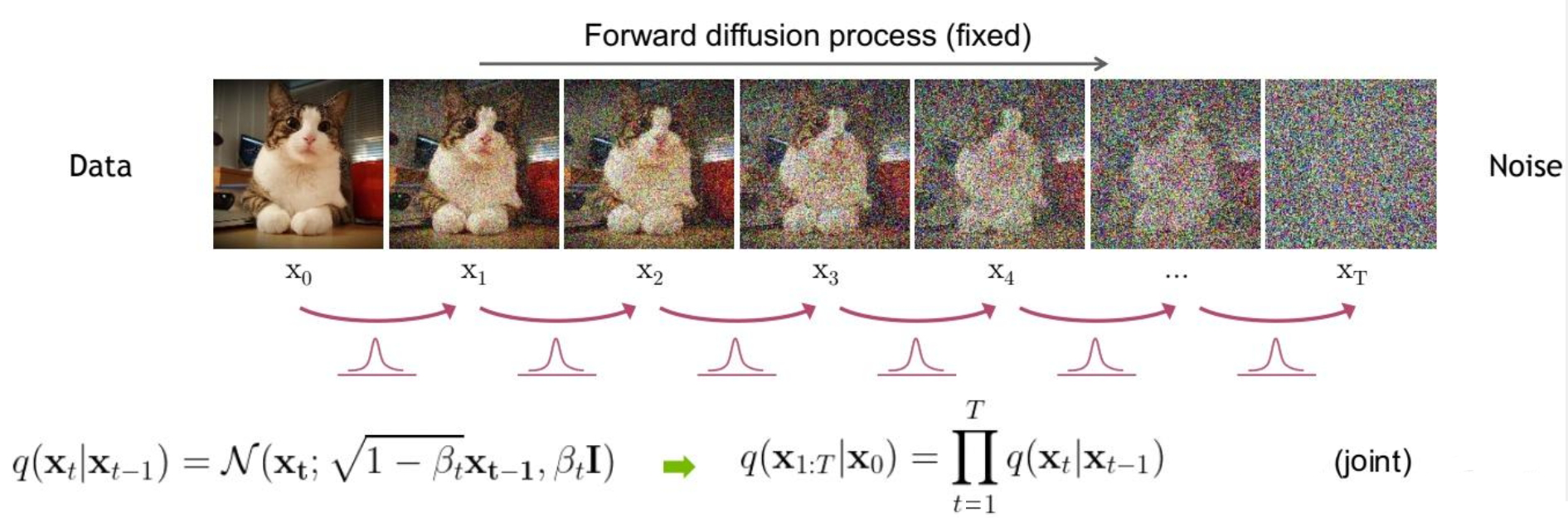
对于原始数据 $\mathbf{x}_0$,其满足初始分布 $ q(\mathbf{x}_0)$,即 $\mathbf{x}_0\sim q(\mathbf{x}_0)$
从该数据出发,总共进行 $T$ 步的扩散过程,即对于 $t\in [1,T]$ 时刻,$\mathbf{x}_{t}$ 和 $\mathbf{x}_{t-1}$ 满足:
其中,$\beta_t$ 为扩散系数,随 $t$ 的增加而增大,$\epsilon\sim \mathcal{N}(\mathbf{0},\mathbf{1)}$ 为高斯噪声
令 $\alpha_t=1-\beta_t$,则有:
根据高斯分布的叠加性,有:
故 $\mathbf{x}_t$ 可化简为:
以此类推,可得:
令 $\overline{\alpha}_t=\alpha_{t}\alpha_{t-1}\cdots\alpha_{1}\alpha_{0}$,则有:
其是一个由原始数据 $\mathbf{x}_0$ 和噪声变量 $\epsilon$ 的线性组合
写为概率分布的形式,有:
$\mathbf{x}_t$ 可以看作是原始数据 $\mathbf{x}_0$ 和随机噪声 $\epsilon$ 的线性组合,$\sqrt{\overline{\alpha}_t}$ 和 $\sqrt{1-\overline{\alpha}_t}$ 为组合系数,它们的平方和为 $1$,这样通过设定 $\overline{\alpha}_t$ 即可直接基于原始数据 $\mathbf{x}_0$ 对任意 $t$ 步的 $\mathbf{x}_t$ 进行采样,相比于设定 $\beta_t$ 一步步进行采样更加直接
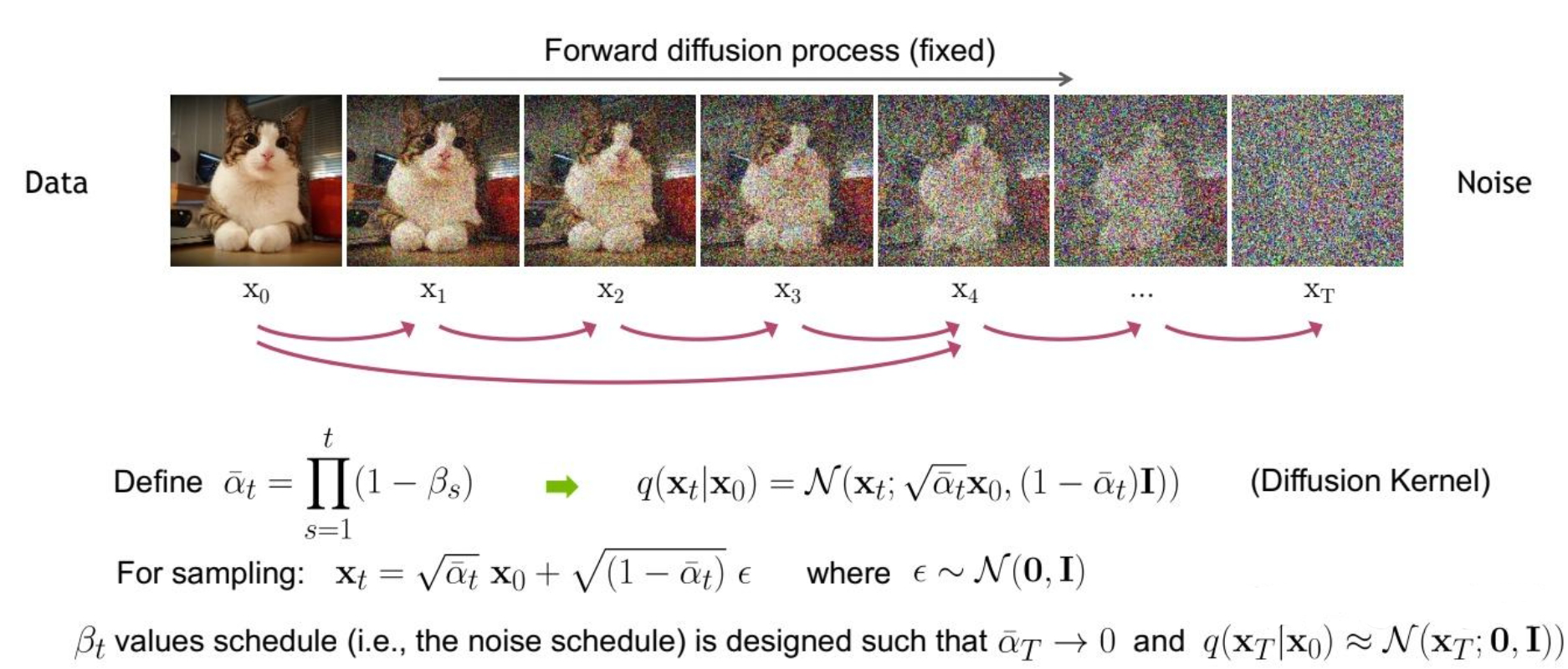
由于 $\beta_t$ 随着时间步 $t$ 的增加而增大,那么 $\alpha_t=1-\beta_t$ 则随着时间步 $t$ 的增加而减小,当 $t\rightarrow T$ 时,$\overline{\alpha}_t=\alpha_{t}\alpha_{t-1}\cdots\alpha_{1}\alpha_{0}\rightarrow 0$,进而有 $\mathbf{x}_T\rightarrow \epsilon$
所以可以认为,在前向扩散过程中,当时间步 $t$ 足够大时,最终产生的图片 $\mathbf{x}_T$ 近似于高斯分布
综上所述,DDPM 的前向扩散过程为:
其中,$\mathbf{x}_0$ 为原始数据,$q(\mathbf{x}_0)$ 为初始分布, $\overline{\alpha}_t=\alpha_{t}\alpha_{t-1}\cdots\alpha_{1}\alpha_{0},\alpha_t=1-\beta_t$,$\beta_t$ 为扩散系数,随 $t$ 的增加而增大,$\epsilon\sim \mathcal{N}(\mathbf{0},\mathbf{1)}$ 为高斯噪声
反向生成过程
对于反向生成过程,其是一个去噪过程,需要根据当前时刻的图片去预测前一时刻的图片,即去除一部分噪声,还原到上一时刻的图片
也就是说,如果知道反向过程中每一步的真实分布 $p(\mathbf{x}_{t-1}|\mathbf{x}_t)$,那么从一个随机噪声 $\mathbf{x}_T\sim \mathcal{N}(\mathbf{0},\mathbf{I})$ 开始,逐渐去除噪声,就能生成一个真实的样本

在整个反向过程中,由于并不知道上一时刻 $\mathbf{x}_{t-1}$ 的值,只能通过当前时刻的值 $\mathbf{x}_t$ 进行预测,因此以概率的形式,采用变分推断(Variational Inference)的方式,利用 $q(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 去近似 $p(\mathbf{x}_{t-1}|\mathbf{x}_t)$,并通过神经网络去拟合 $q(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 的参数,一步步优化使其与后验分布 $p(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 相似
对于后验分布 $q(\mathbf{x}_{t-1}|\mathbf{x}_t)$,利用贝叶斯公式,有:
在已知原图 $\mathbf{x}_{0}$ 的情况下,上式可写为:
此时,等式右边的概率均为先验分布
根据马尔可夫链的无后效性,与扩散概率模型中的前向过程,有:
根据 DDPM 得到的前向扩散过程 $q(\mathbf{x}_{t}|\mathbf{x}_{0}) =\mathcal{N}(\mathbf{x}_t;\sqrt{\overline{\alpha}_t}\mathbf{x}_0,(1-\overline{\alpha}_t)\mathbf{I})$ 可知:
因此,$q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})$ 可写为:
由于 $\alpha_t=1-\beta_t$,故有:
根据高斯分布的概率密度函数 $f(x)=\frac{1}{\sqrt{2\pi}}\exp[-\frac{(x-\mu)^2}{2\sigma^2}]$ 进行展开,有:
由于 $\mathbf{x}_{t-1}$ 才是要关注的变量,因此将上式整理为关于 $\mathbf{x}_{t-1}$ 的形式,即:
其中,$C(\mathbf{x}_t,\mathbf{x}_0)$ 与 $\mathbf{x}_{t-1}$ 无关,只影响成正比的系数
由于标准高斯分布 $\mathcal{N}(\mathbf{0},\mathbf{1})\propto \exp [-\frac{1}{2}\frac{\mathbf{x}^2-2\mathbf{x}\mu+\mu^2}{\sigma^2}]$,那么对于上式,易得:
对上式进行化简,可得:
根据 DDPM 的前向过程 $\mathbf{x}_t = \sqrt{\overline{\alpha}_t} \mathbf{x}_{0} + \sqrt{1-\overline{\alpha}_t}\epsilon$,将上式中的 $\mathbf{x}_0$ 进行替换,有:
综上所述,对于后验概率 $q(\mathbf{x}_{t-1}|\mathbf{x}_t)$,只需要拟合均值和方差
即:
其中,均值 $\mu$ 依赖于当前时刻的值 $\mathbf{x}_t$ 和高斯噪声 $\epsilon_{\theta}(\mathbf{x}_t,t)$,方差 $\sigma^2$ 是一个由前向扩散过程 $\alpha_t$ 固定的定量,也就是说,只需要使用神经网络去拟合高斯分布 $\epsilon_{\theta}(\mathbf{x}_t,t)$
综上所述,DDPM 的反向生成过程为:
其中,$\mathbf{x}_T$ 为生成数据,$q(\mathbf{x}_{t-1}|\mathbf{x}_{t})$ 为 $p(\mathbf{x}_{t-1}|\mathbf{x}_{t})$ 的变分推断后的近似分布,$\overline{\alpha}_t=\alpha_{t}\alpha_{t-1}\cdots\alpha_{1}\alpha_{0},\alpha_t=1-\beta_t$,$\beta_t$ 为扩散系数,随 $t$ 的增加而增大,$\epsilon\sim \mathcal{N}(\mathbf{0},\mathbf{1)}$ 为高斯噪声
【优化目标】
变分下界
上面介绍了 DDPM 的前向扩散过程和反向生成过程,现在从另一个角度来看扩散模型:如果将中间产生的变量看成隐变量,那么扩散模型其实是包含 $T$ 个隐变量的隐变量模型(Latent Variable Model),可以看作是一个特殊的多层变分自编码器(Hierarchical VAE)
前向扩散过程可以视为编码器 Encoder,反向生成过程可以视为解码器 Decoder,隐变量是与原始数据 $\mathbf{x}_0\sim q(\mathbf{x}_0)$ 同维度的中间变量 $\mathbf{x}_t$
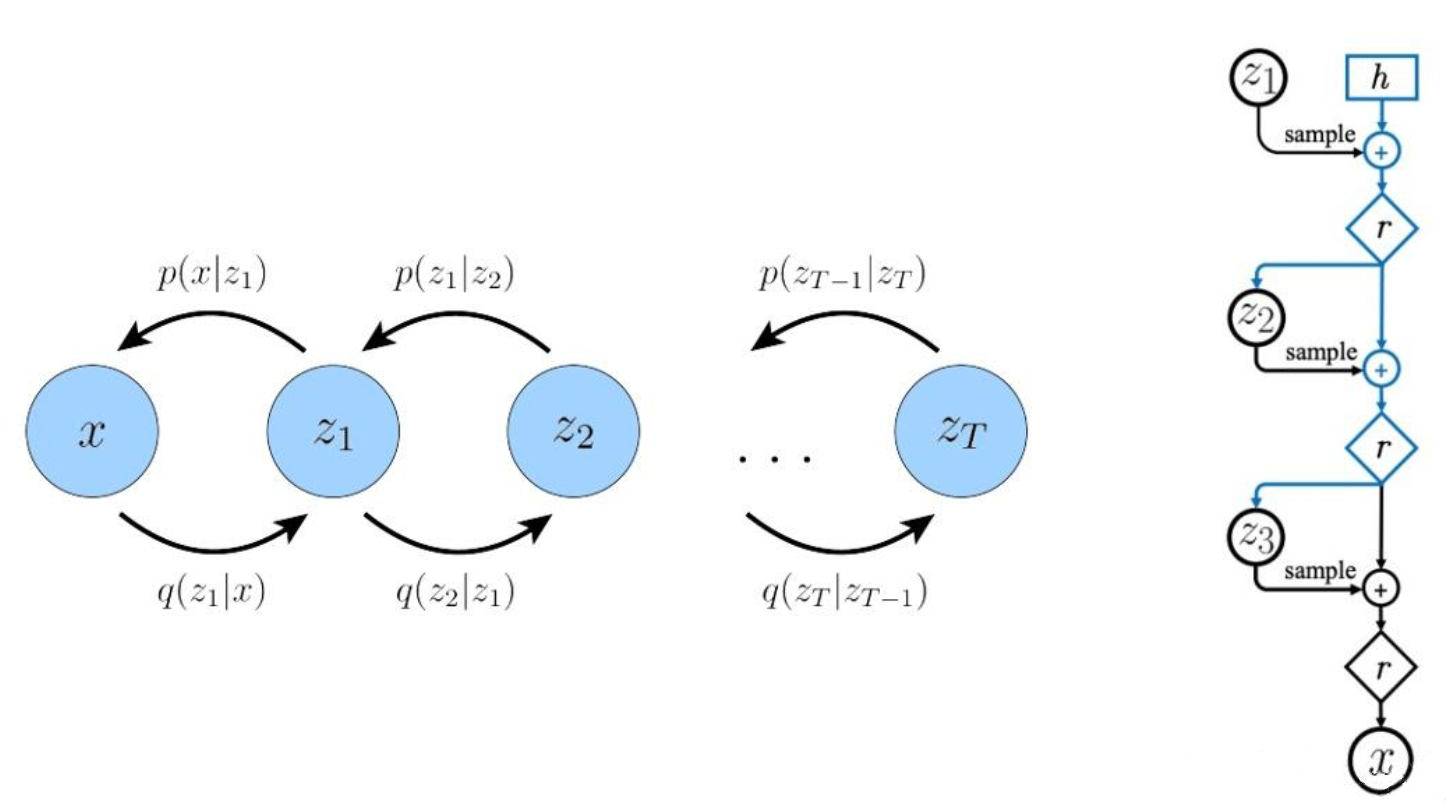
从这一角度出发,对于扩散模型 $p(\mathbf{x}_{0}) = \int p(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T}$ 就可以基于变分推断来得到变分上界 VLB,即:
对于网络训练来说,其训练目标为 VLB 取负,即:
进一步对其分解,有:
由于马尔可夫的无后效性,且 $\mathbf{x}_0$ 已知,故 $=q(\mathbf{x}_t|\mathbf{x}_{t-1})=q(\mathbf{x}_t|\mathbf{x}_{t-1},\mathbf{x}_0)$,进而有:
利用贝叶斯公式,有:
进一步化简,有:
此时可以看到,最终的优化目标共 $T+1$ 项
$L_0$:原始数据重建
对于优化目标:
其中,$L_0$ 可以看作是原始数据重建,优化的是负对数似然,其可以用估计的 $\mathcal{N}(\mathbf{x}_0;f_{\mu}(\mathbf{x}_1,1),f_{\Sigma}(\mathbf{x}_1,1))$ 来构建一个离散化的 Decoder 来计算,即:
在 DDPM 中,会将原始图像的像素值从 $[0, 255]$ 范围归一化到 $[-1, 1]$,这样不同的像素值之间的间隔其实就是 $\frac{2}{255}$,就可以计算高斯分布落在以真实数据为中心且范围大小为 $\frac{2}{255}$ 时的概率积分(概率密度函数的积分)
$L_t$:噪声分布与先验分布的 KL 散度
对于优化目标:
其中,$L_T$ 计算的是最后得到的噪声分布和先验分布的 KL 散度,由于先验 $p(\mathbf{x}_T)=\mathcal{N}(\mathbf{0},\mathbf{I})$,扩散过程最后得到的随机噪声 $q(\mathbf{x}_T|\mathbf{x}_0)$ 也近似于 $\mathcal{N}(\mathbf{0},\mathbf{I})$,因此这个 KL 散度没有训练参数,近似为 $0$
$L_{t-1}$:估计分布与后验分布的 KL 散度
对于优化目标:
其中,$L_{t-1}$ 计算的是估计分布 $p(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 和真实的后验分布 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x})_0$ 的 KL 散度,这里希望估计的去噪过程和依赖真实数据的去噪过程近似一致:
之所以将 $p(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 定义为一个用网络参数化的高斯分布 $\mathcal{N}(\mathbf{x}_{t-1};f_{\mu}(\mathbf{x}_t,t);f_{\Sigma}(\mathbf{x}_t,t))$,是因为要匹配的后验分布 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$ 也是一个高斯分布,对于训练目标 $L_0$ 和 $L_{t-1}$ 来说,都是希望得到训练好的网络的均值 $f_{\mu}(\mathbf{x}_t,t)$ 和方差 $f_{\Sigma}(\mathbf{x}_t,t)$
上文提到过,DDPM 对 $p(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 做了进一步简化,采用固定的方差 $f_{\Sigma}(\mathbf{x}_t,t)=\sigma^2_t\mathbf{I}$, $\sigma^2_t$ 是一个由前向扩散过程 $\alpha_t$ 固定的定量,故有:
那么对于两个高斯分布 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$ 和 $p(\mathbf{x}_{t-1}|\mathbf{x}_t) $ 的 KL 散度就有:
那么优化目标 $L_{t-1}$ 即为:
也就是说,希望网络学习到的均值 $f_{\tilde{\mu}}(\mathbf{x}_t,\mathbf{x}_0)$ 和后验分布的均值 $f_{\mu}(\mathbf{x}_t,t)$ 一致
根据 DDPM 的前向扩散过程 $\mathbf{x}_t(\mathbf{x}_0,\epsilon) = \sqrt{\overline{\alpha}_t} \mathbf{x}_{0} + \sqrt{1-\overline{\alpha}_t}\epsilon$,将其带入到 $L_{t-1}$ 中的 $f_{\tilde{\mu}}(\mathbf{x}_t,\mathbf{x}_0)$,有:
化简可得:
进一步,采用 VAE 中的重参数化技巧,将 $f_{\mu}(\mathbf{x}_t(\mathbf{x}_0,\epsilon),t)$ 重参数化,有:
其中,$\epsilon_{\theta}$ 是一个基于神经网络的拟合函数,这意味着由原来的预测均值而换成预测噪音
再将重参数化后的 $f_{\mu}(\mathbf{x}_t(\mathbf{x}_0,\epsilon),t)$ 带入优化目标,可以得到:
进一步对上式进行简化,去掉权重系数,故有:
由于去掉了不同的权重系数,所以这个简化的目标其实是 VLB 的优化目标进行了 reweight
从 DDPM 的对比实验结果来看,预测噪音比预测均值效果要好,采用简化版本的优化目标比 VLB 目标效果要好
【模型训练】
对于 DDPM 来说,前向扩散过程和反向生成过程的核心是:
从这两个核心公式中可以看出,无论是前向过程还是反向过程,与 $\alpha_t$ 相关的都是常数,唯一不确定的就是 $\epsilon_{\theta}(\mathbf{x}_t,t)$
重新考虑前向扩散过程,能否从当前样本 $\mathbf{x}_t$ 中提取出 $\epsilon_{\theta}(\mathbf{x}_t,t)$?显然,这个想法具备可行性,因为 $\mathbf{x}_t$ 本身就是一张图片,可以使用卷积神经网络进行提取
在 DDPM 中,这一过程采用的是 Unet+Self-attention,其中 Unet 利用当前样本 $\mathbf{x}_t$ 和时间步 $t$ 预测噪声,即使用 Unet 来实现对 $\epsilon_{\theta}(\mathbf{x}_t,t)$ 的预测,整个训练过程其实就是在训练 Unet 网络的参数
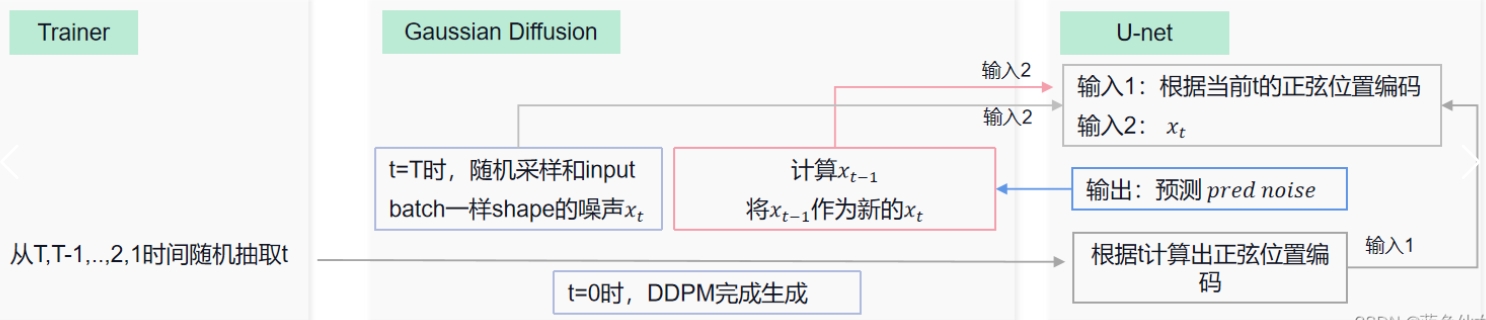
如下图所示,整个 DDPM 模型可分为训练和采样两大算法

具体来说,对于 Unet 的训练过程如下:
- 从训练数据中抽取一个样本 $\mathbf{x}_0$
- 从 $1\sim T$ 中随机抽取一个时间步 $t$
- 根据前向过程,随机采样一个噪声,加到 $\mathbf{x}_0$ 上,形成加噪样本 $\mathbf{x}_t$
- 将加噪样本 $\mathbf{x}_t$ 和时间步 $t$ 输入到 Unet 中,Unet 根据时间步 $t$ 生成正弦位置编码与 $\mathbf{x}_t$ 结合,预测加的这个噪声
- 将 Unet 预测的噪声与之前随机采样的噪声求 L2 损失,计算梯度,更新权重
- 重复上述步骤,直到完成训练
训练步骤中每个模块的交互如下图:
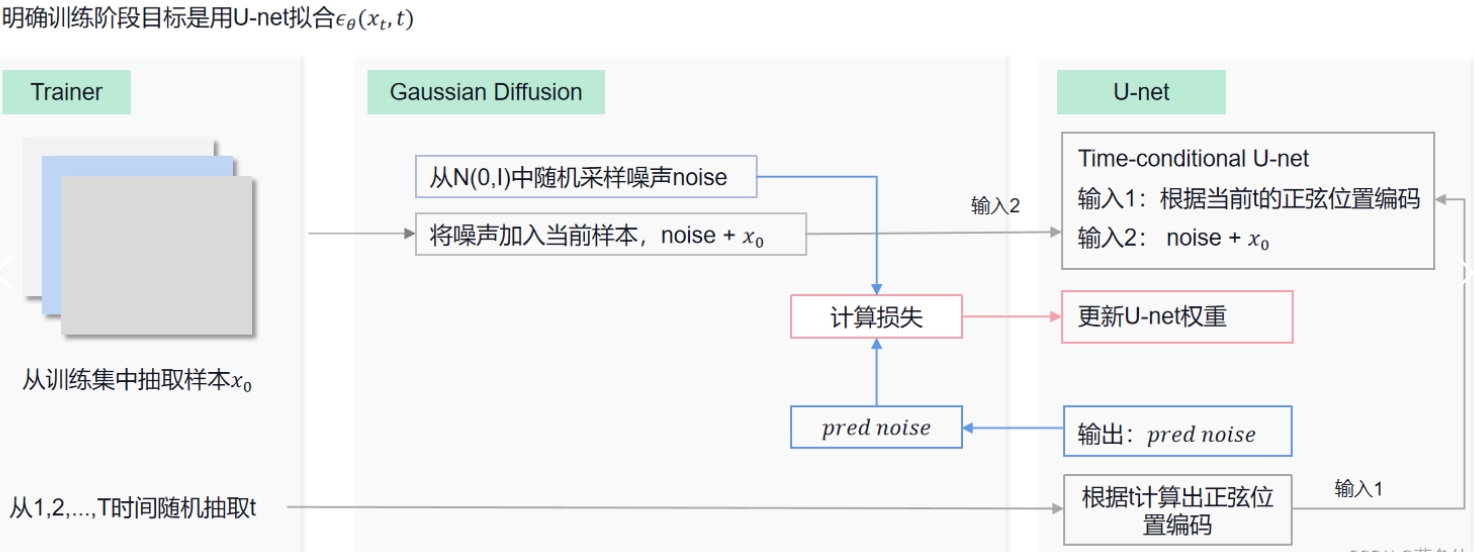
对于 Unet 的采样过程如下:
- 从标准正态分布采样出 $x_T$
- 从 $T,T-1,…,2,1$ 依次重复以下步骤:
- 从标准正态分布 $Z\sim\mathcal{N}(\mathbf{0},\mathbf{I})$ 中采样 $z$,为重参数化做准备
- 根据模型求出重参数化后的 $\epsilon_{\theta}$,并计算 $x_{t-1}$
- 循环结束后返回 $\mathbf{x}_0$
采样步骤中每个模块的交互如下图: