去噪扩散隐式模型 DDIM

【概述】

对于 DDPM 来说，一个最大的缺点是需要设置较长的扩散步数才能得到好的效果，这导致了生成样本的速度较慢，比如扩散步数为 $1000$ 的话，那么生成一个样本就要模型推理 $1000$ 次

为此 Jiaming Song 等学者在《Denoising Diffusion Implicit Models》 中针对 DDPM 进行了改进，提出了去噪扩散隐式模型（Denoising Diffusion Implicit Models，DDIM），不再限制前向和反向过程必须是马尔卡夫链，在不牺牲质量的情况下，允许更少的采样步数来加速反向生成过程

此外 DDIM 的另一个特点是从一个随机噪音生成样本的过程是一个确定的过程，即中间再额外没有加入随机噪音

【引入】

对于 DDPM 的简化优化目标：

$$L_{t-1}^{\text{simple}} = \mathbb{E}_{\mathbf{x}_0,\epsilon\sim\mathcal{N}(\mathbf{0},\mathbf{I})} \Big[ \parallel \epsilon - \epsilon_{\theta} (\sqrt{\overline{\alpha}_t} \mathbf{x}_{0} + \sqrt{1-\overline{\alpha}_t}\epsilon,t) \parallel^2 \Big] \\$$

可以发现，DDPM 其实仅依赖于边缘分布 $q(\mathbf{x}_t|\mathbf{x}_0)$，而不是直接作用在联合分布 $q(\mathbf{x}_{1:T}|\mathbf{x}_0)$ 上，也就是说 DDPM 这个隐变量模型可以有很多推理分布来选择，只要推理分布满足边缘分布条件（扩散过程的特性）即可，而且这些推理过程并不一定要是马尔可夫链

需要注意的是，要得到 DDPM 的优化目标，还需要知道后验分布 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$，在 DDPM 中，这个分布的推导是依赖于马尔可夫链和 $q(\mathbf{x}_t|\mathbf{x}_0)$ 得到的，如果要解除对前向过程的依赖，就需要直接定义 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$ 这个分布

【原理】

非马尔可夫前向扩散过程

根据 DDPM 的前向扩散过程：

$$\begin{gather*} q(\mathbf{x}_{0:T}) = q(\mathbf{x}_0) \prod_{t=1}^T q(\mathbf{x}_t|\mathbf{x}_{t-1}) \\ q(\mathbf{x}_{t}|\mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t};\sqrt{\overline{\alpha}_t}\mathbf{x}_{0},(1-\overline{\alpha}_t)\mathbf{I}) \\ \mathbf{x}_0 \sim q(\mathbf{x}_0) \end{gather*}$$

DDIM 令 $\alpha_t=\overline{\alpha}_t$，根据推导（详见论文附录），将前向扩散分布定义为：

$$\begin{align*} &q_{\sigma}(\mathbf{x}_{1:T}|\mathbf{x}_0) = q_{\sigma}(\mathbf{x}_T|\mathbf{x}_0)\prod_{t=2}^T q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0) \\ &q_{\sigma}(\mathbf{x}_{T}|\mathbf{x}_{0}) = \mathcal{N}(\sqrt{\alpha_T}\mathbf{x}_{0},(1-\alpha_T)\mathbf{I}) \\ &q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)=\mathcal{N}\left(\sqrt{\alpha_{t-1}}\mathbf{x}_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2}\cdot\frac{\mathbf{x}_t-\sqrt{\alpha_t}\mathbf{x}_0}{\sqrt{1-\alpha_t}},\sigma_t^2I\right),\quad t\geq 2 \end{align*}$$

其中，方差 $\sigma_t^2$ 是一个实数，不同的值代表了不同的高斯分布，因此 $q_{\sigma}(\mathbf{x}_{1:T}|\mathbf{x}_0) $​ 其实是一系列的前向扩散分布，而均值也被定义为依赖于 $\mathbf{x}_0$ 和 $\mathbf{x}_t$​ 的组合函数

根据 $q(\mathbf{x}_T|\mathbf{x}_0)$，根据数学归纳法，可以得到对于所有 $t$，均满足：

$$q(\mathbf{x}_t|\mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t;\sqrt{\alpha_t}\mathbf{x}_{0},(1-\alpha_t)\mathbf{I})$$

也就是说，这里虽然没有直接定义前向扩散过程，但满足了之前提到的两个条件：

1. 已知边缘分布 $q(\mathbf{x}_t|\mathbf{x}_0)$
2. 已知后验分布 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$

此时，得到的前向扩散过程是一个非马尔可夫链的前向扩散过程，同时采用与 DDPM 一样的方式去推导优化目标，最终也会得到相同的 $L_{t-1}^{\text{simple}}$

如下图所示，给出了非马尔可夫前向扩散过程的示例

非马尔可夫反向生成过程

根据 DDPM 的反向生成过程：

$$\begin{gather*} p(\mathbf{x}_{0:T}) = p(\mathbf{x}_{T})\prod_{t=1}^T p(\mathbf{x}_{t-1}|\mathbf{x}_{t}) \\ q(\mathbf{x}_{t-1}|\mathbf{x}_t) \sim \mathcal{N}(\frac{1}{\sqrt{\alpha}_t} \Big[ \mathbf{x}_t - \frac{1-\alpha_t}{\sqrt{1-\overline{\alpha}_t}} \epsilon_{\theta}(\mathbf{x}_t,t) \Big],\frac{(1-\alpha_{t})(1-\overline{\alpha}_{t-1})}{(1-\overline{\alpha}_{t})}) \\ \mathbf{x}_T \sim\mathcal{N}(\mathbf{x}_T;\mathbf{0},\mathbf{I}) \end{gather*}$$

根据 $q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$ 的形式，可使用如下公式来从 $\mathbf{x}_t$ 生成 $\mathbf{x}_{t-1}$：

$$\mathbf{x}_{t-1}=\sqrt{\alpha_{t-1}}\Big(\underbrace{\frac{\mathbf{x}_t-\sqrt{1-\alpha_t}\epsilon_\theta(\mathbf{x}_t,t)}{\sqrt{\alpha_t}}}_{\text{predicted }\mathbf{x}_0}\Big)+\underbrace{\sqrt{1-\alpha_{t-1}-\sigma_t^2}\cdot\epsilon_\theta(\mathbf{x}_t,t)}_{\text{direction pointing to }\mathbf{x}_t}+\underbrace{\sigma_t\epsilon_t}_{\text{random noise}}$$

这个过程分为三个部分：

1. 由预测的 $\mathbf{x}_0$ 来产生
2. 指向 $\mathbf{x}_t$ 的部分（$\epsilon_{\theta}(\theta{x}_t,t)$ 是与 $\mathbf{x}_t$ 无关的噪声）
3. 随机噪声

进一步，将 $\sigma_t^2$ 定义为：

$$\sigma_t^2=\eta\cdot\tilde{\beta}_t=\eta\cdot\sqrt{\frac{1-\alpha_{t-1}}{1-\alpha_t}}\sqrt{\frac{1-\alpha_t}{\alpha_{t-1}}}$$

当 $\eta=1$ 时，$\sigma_t^2=\tilde{\beta}_t$，此时反向生成过程与 DDPM 相同；当 $\eta=0$ 时，这个时候反向生成过程就没有随机噪声了，一旦最初的与 $\mathbf{x}_t$ 无关的噪声 $\epsilon_{\theta}(\theta{x}_t,t)$ 确定，那么样本生成就变成了一个确定性的过程，这种情况即 DDIM

【反向生成过程的加速】

虽然 DDIM 和 DDPM 的训练过程一样，但 DDIM 并没有明确的前向扩散过程，这意味着可以定义一个更短时间步 $t$ 的前向扩散过程

对于原始序列 $t=[1,2,\cdots,T]$，采样一个长度为 $S$ 的子序列 $\tau=[\tau_1,\tau_2,\cdots,\tau_S]$，将 $\mathbf{x}_{\tau_1},\mathbf{x}_{\tau_2},\cdots,\mathbf{x}_{\tau_S}$ 的前向扩散过程定义为一个马尔可夫链，且满足：

$$q(\mathbf{x}_{\tau_1}|\mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t};\sqrt{\alpha_{\tau_i}}\mathbf{x}_0,(1-\alpha_{\tau_i})\mathbf{I})$$

如下图所示，展示了 $\tau=[1,3]$ 的前向扩散过程

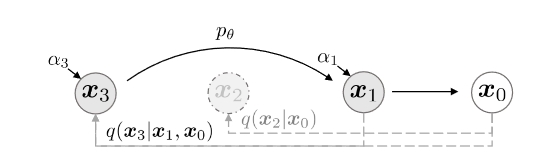
那么，反向生成过程就可以用这个子序列的反向马尔可夫链来替代，由于可以设置比原来的步数要小，就可以加速反向生成过程

$$\mathbf{x}_{\tau_{i-1}}=\sqrt{\alpha_{\tau_{i-1}}}\Big(\frac{\mathbf{x}_{\tau_{i}}-\sqrt{1-\alpha_{\tau_{i}}}\epsilon_{\theta}(\mathbf{x}_{\tau_{i}},\tau_{i})}{\sqrt{\alpha_{\tau_{i}}}}\Big)+\sqrt{1-\alpha_{\tau_{i-1}}-\sigma_{\tau_{i}}^{2}}\cdot\epsilon_{\theta}(\mathbf{x}_{\tau_{i}},\tau_{i})+\sigma_{\tau_{i}}\epsilon$$

本质上来说，上述的加速，其实是将前向扩散过程按照如下方式进行了分解，一个是由 $\{\mathbf{x}_{\tau_i}\}_{i=1}^S$ 组成的马尔可夫链，另一个是由剩余变量 $\{\mathbf{x}_t\}_{t\in\overline{\tau}}$ 组成的星状图

$$q_{\sigma,\tau}(\mathbf{x}_{1:T}|\mathbf{x}_0)=q_{\sigma,\tau}(\mathbf{x}_T|\mathbf{x}_0)\prod_{i=1}^Sq_\sigma(\mathbf{x}_{\tau_{i-1}}|\mathbf{x}_{\tau_i},\mathbf{x}_0)\prod_{t\in\bar{\tau}}q_{\sigma,\tau}(\mathbf{x}_t|\mathbf{x}_0)$$

其中，$\overline{\tau}=\{1,2,\cdots,T\}-\tau$

同时，对于反向生成过程，也只用马尔可夫链的那部分进行生成：

$$p_\theta(\mathbf{x}_{0:T})=p(\mathbf{x}_T)\underbrace{\prod_{i=1}^Sp_\theta(\mathbf{x}_{\tau_{i-1}}|\mathbf{x}_{\tau_i})}_{\text{use to produce sample}}\times\underbrace{\prod_{t\in\bar{\tau}}p_\theta(\mathbf{x}_0|\mathbf{x}_t)}_{\text{only for VLB}}$$