References：

Deep Residual Learning for Image Recognition

（二十七）通俗易懂理解——Resnet残差网络

ResNet 详解

残差神经网络（ResNet）

深度学习之残差神经网络（ResNet）

你必须要知道CNN模型：ResNet

经典CNN结构简析：AlexNet、VGG、NIN、GoogLeNet、ResNet etc.

一文读懂LeNet、AlexNet、VGG、GoogleNet、ResNet到底是什么？

【概述】

ResNet 残差神经网络是由微软研究院的何恺明等人提出的，获得了 2015 年 ImageNet 比赛的冠军，其将图像分类识别错误率降低到了 $3.6\%$，这个结果甚至超出了正常人眼识别的精度

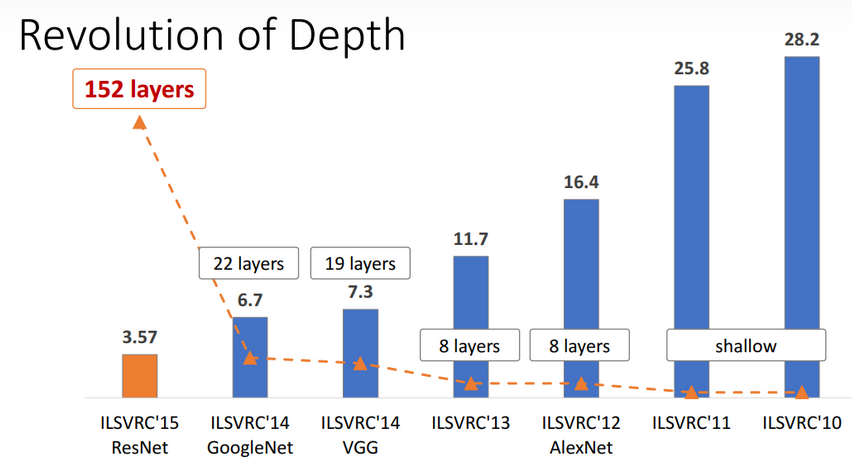
ResNet 的最大贡献是发现了退化现象（Degradation），并针对退化现象构建了带有快捷连接（Shortcut Connection）的残差模块，极大的消除了深度过大的神经网络训练困难问题，使得神经网络的深度首次突破了 $100$ 层、最大的神经网络甚至超过了 $1000$ 层

【退化现象】

自 2012 年的 ILSVRC 挑战赛 AlexNet 取得冠军后，随着 VGG、GoogLeNet 等深度神经网络以及各种 Inception 结构的扩展，网络层次在不断加深，网络结构也越来越复杂

那么，网络层次的加深是否一定能取得更好的效果？

从理论上来说，这是正确的

假设存在一个浅层网络，现在想要通过向上堆积新层来建立深层网络，一个极端的情况是新加的这些层什么也不学习，仅复制浅层网络的特征，即新加的层均是恒等映射（Identity Mapping）的网络层，在这种情况下，新生成的深层网络至少应该与原来的浅层网络性能一样

换句话说，原网络的解，只是新网络的解的子空间，在新网络解的空间中应该能找到比原网络解的子空间更好的结果

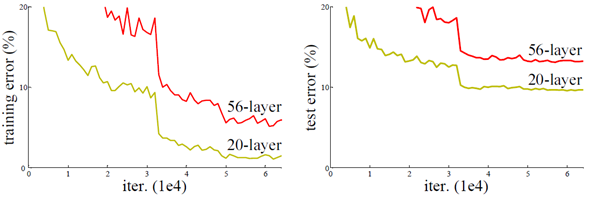
但实践表明，在增加网络层数后，训练误差往往不降反升，这种现象被 ResNet 团队称为退化现象（Degradation）

与传统的机器学习相比，深度学习的关键在于网络层数更深、非线性转换（激活函数）、自动的特征提取和特征转换，其中，非线性转换是关键目标，它将数据映射到高纬空间以便于更好的完成数据分类

但随着网络深度的不断增大，所引入的激活函数也越来越多，数据被映射到更加离散的空间，此时已经难以让数据回到原点（恒等变换），换句话说，神经网络将这些数据映射回原点所需要的计算量，已经远超我们所能承受的

非线性转换极大的提高了数据分类能力，但随着网络的深度不断的加大，在非线性转换方面已经走的太远，以至于无法实现线性转换

显然，在神经网络中增加线性转换分支成为很好的选择，于是，ResNet 团队提出了具有快捷连接（Shortcut Connection）的残差模块，在线性转换和非线性转换之间寻求一个平衡

【残差模块】

结构

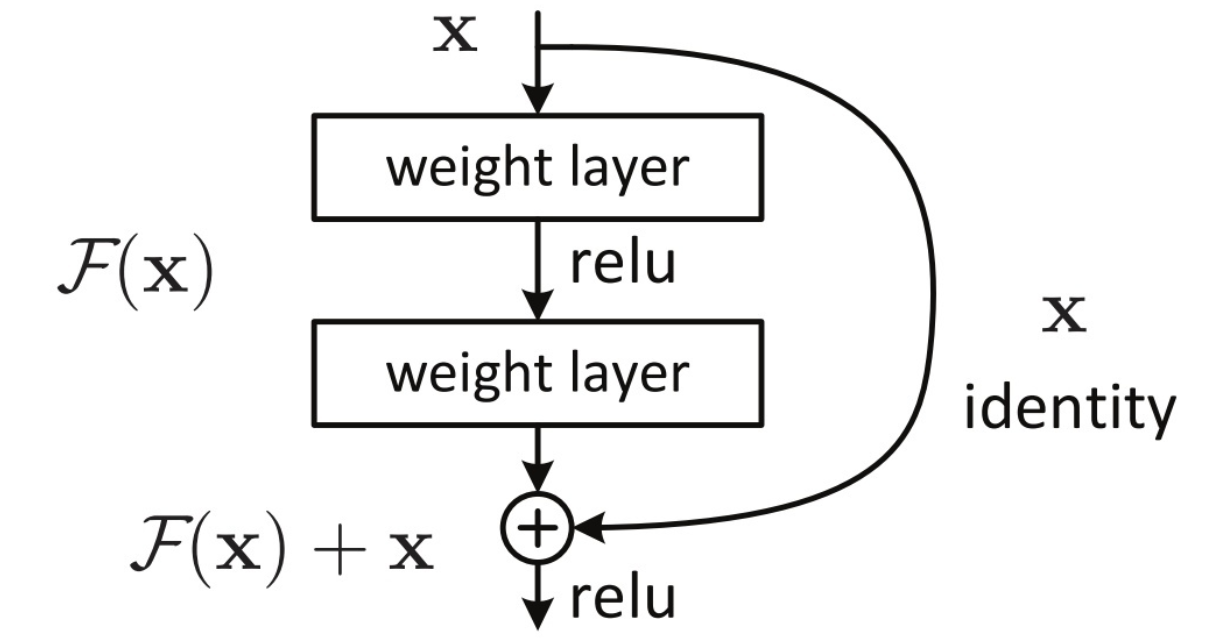
假设对于一个几层堆积而成的堆积层结构，当输入为 $x$ 时学习到的最优函数为 $H(x)$，希望可以学习到的残差函数为 $F(x)=H(x)-x$，此时原始的学习特征为 $F(x)+x$

这样是因为通过残差学习比通过原始特征学习跟容易，极端情况下，当残差 $F(x)=0$ 时，堆积层相当于仅做了恒等变换 $y=x$，至少网络性能不会下降

但实际上，由于残差 $F(x)$ 不会为 $0$，这就使得堆积层在输入特征基础上能够学习到新的特征，从而拥有更好的性能

残差块的结构如下图所示，其中恒等函数部分被称为快捷连接（Shortcut Connection），由于类似于电路中的短路，也被称为短路机制

数学表达

对应到神经网络中，残差块可表示为：

$\begin{gather*} Z^{[l]} = h(A^{[l-1]}) + F(A^{[l-1]},W^{[l]}) \\ A^{[l]} = \text{ReLU}(Z^{[l]}) \end{gather*}$

其中，$A^{[l]}$ 代表第 $l$ 个残差单元的输出，$h(A^{[l-1]})=A^{[l-1]}$ 代表恒等映射，$W^{[l]}$ 代表第 $l$ 个残差单元内的所有权重，$F(\cdot)$ 为残差函数，代表学习到的残差

基于上式，从浅层 $l$ 到深层 $l_n$ 学习到的特征为：

$A^{[l_n-1]} = A^{[l-1]} + \sum_{i=l}^{l_n-1} F(A^{[i-1]},W^{[l]})$

利用链式规则，可以求得反向传播过程的梯度，即：

$\begin{align*} \frac{\partial Loss}{\partial A^{[l-1]}} &= \frac{\partial Loss}{\partial A^{[l_n-1]}} \cdot \frac{\partial A^{[l_n-1]}}{\partial A^{[l-1]}} \\ &= \frac{\partial Loss}{\partial A^{[l_n-1]}} \cdot \Big( 1+ \frac{\partial}{\partial A^{[l-1]}} \sum_{i=l}^{l_n-1} F(A^{[i-1]},W^{[l]}) \Big) \end{align*}$

其中，$\frac{\partial Loss}{\partial A^{[l_n-1]}}$ 表示损失函数到达第 $l_n$ 层的梯度，括号中的 $1$ 说明通过快捷连接可以无损地传播梯度，而另外一项残差梯度则需要经过带有残差块权重 $W^{[l]}$ 的层，梯度不是直接传递过来的

而残差梯度不会那么巧全为 $-1$，而且就算其比较小，由于有 $1$ 的存在也不会由于网络太深而出现梯度消失问题，因此残差学习会更容易

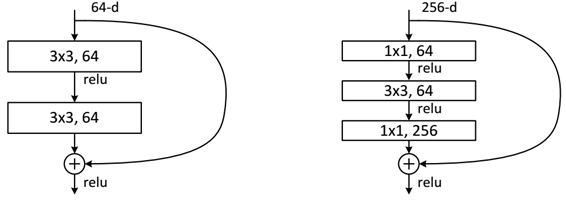
此外，在全连接层中，如果激活函数的维度与第 $l$ 个残差单元的输出 $A^{[l]}$ ，那么可以用一个变换矩阵 $W^{[l]}_t$ 相乘，即对 $A^{[l]}$ 进行线性映射，如果在卷积层中两者维度不同，那么可以使用 $1\times1$ 卷积核和零填充来进行维度变换

实现

ResNet 沿用了 VGG 的 $3\times3$ 卷积层设计，并使用了 Batch Normalization 层和 ReLU 激活函数，此外引入了额外的 $1\times1$ 卷积层将输入变换为需要的形状，与残差函数结果直接相加

残差块的 torch 实现如下，其继承了 nn.Module，因此可以直接将其作为 nn.Sequential() 的参数来设计网络

import torch
from torch import nn
from torch.nn import functional as F

class Residual(nn.Module):
    def __init__(self, input_channels, num_channels, use_conv=False, strides=1):
        super().__init__()
        
        self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3, padding=1)
        
        # 判断是否需要改变输入形状
        if use_conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1)
        else:
            self.conv3 = None

        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)
    
    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

如下图所示，此代码生成两种类型的网络，分别对应形状一致和不同的情况，通过 use_conv 来判断是否改变输入的形状

【网络架构】

ResNet 网络在 VGG19 的基础上进行构建的，并进行了如下改变：

在每两层间增加快捷连接机制，形成残差块
使用步长 stride=2 的卷积进行下采样
使用全局平均池化 GAP 层替代全连接层
当特征图大小降低一半时，特征图数量增加一倍，以保持网络的复杂度

如下图所示，展示了 VGG19 和 ResNet34 的架构对比

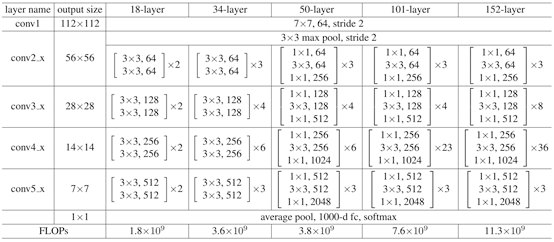
不同深度的 ResNet 参数表如下所示，从表中可以看到，对于 ResNet18 和 ResNet34，进行的是两层间的残差学习，当网络更深时，进行的是三层间的残差学习，三层卷积核大小分别是 $1\times 1$、$3\times3$、$1\times1$

Alex_McAvoy

经典卷积神经网络之 ResNet

【概述】

【退化现象】

【残差模块】

结构

数学表达

实现

【网络架构】