【问题描述】
在字符串的单模式匹配中,对于待匹配的长度为 $n$ 的数组 T[n]称为文本(Text),对于匹配的满足 $m\leq n$ 的长度为 $m$ 的数组 P[m] 称为模式(Pattern)
当 $0\leq s \leq n-m$ 时,若对于 $1\leq i\leq m$,有 T[s+i]=P[i] 成立,则称 $s$ 为模式 P 在文本 T 中的有效位移(Valid Shift),又称匹配点
如下图所示,要在文本 T=abcabaabcabac 中找出模式 P=abaa 的所有匹配
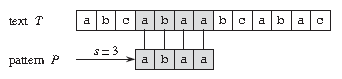
可以发现,模式 P 在文本 T 中,仅在位移 $s=3$ 处出现一次,即 $s=3$ 为一个匹配点
综上,字符串模式匹配,本质上就是对字符串子串的定位操作,其求的是子串在主串中的位置
在字符串模式匹配中,常用的算法有 BF 算法、MP 算法、KMP 算法等,这些算法通常都分为两个步骤:预处理(Preprocessing)、匹配(Matching),所以算法的总时间复杂度为预处理和匹配的时间复杂度的总和
常见的字符串匹配算法有:BP 算法、KMP 算法等
【PM 表】
对于一个字符串,在进行匹配时,有如下基本概念:
- 字符串前缀:除最后一个字符外字符串的头部子串集,当字符串为单个字符时,前缀为空集
- 字符串后缀:除第一个字符外字符串的尾部子串集,当字符串为单个字符时,后缀为空集
- 相等前后缀:字符串前缀与后缀的交集
- 部分匹配值:字符串前缀与后缀的最长的相等前后缀的长度
以 ababa 为例,有:
| 子串 | 前缀 | 后缀 | 相等前后缀 | 部分匹配值 |
|---|---|---|---|---|
a |
∅ |
∅ |
∅ |
$0$ |
ab |
{a} |
{b} |
∅ |
$0$ |
aba |
{a,ab} |
{a,ba} |
{a} |
$1$ |
abab |
{a,ab,aba} |
{a,ab,bab} |
{a,ab} |
$2$ |
ababa |
{a,ab,aba,abab} |
{a,ba,aba,baba} |
{a,aba} |
$3$ |
将一个字符串的全部子串的部分匹配值写成数组形式,即可得到部分匹配值(Partial Match)的表,即 PM 表
在上例中,ababa 的 PM 表为:
| 编号 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 字符 | a | b | a | b | a |
| PM 值 | 0 | 0 | 1 | 2 | 3 |

