【从 BP 算法到 MP 算法】

BP 算法是最简单的模式匹配算法，其本质是暴力枚举

在 BP 算法中，当文本串 T 的某些子串与模式串 P 能部分匹配时，文本串的扫描指针 i 每次都是后移一位再从头开始比较，而当某轮已匹配相等的字符序列是模式串 P 的某个前缀时再进行比较，相当于模式串不断地自我比较

针对上述问题，对 BF 算法进行改进，即得到了 MP（Morris-Pratt）算法，其是以 James Morris 和 Vaughan Pratt 两人的姓来命名的

MP 最大的特点是：只让模式串 P 的指针 j 回溯，让文本串 T 的指针 i 不变

如下图所示，文本串的 C 与模式串的 B 不匹配

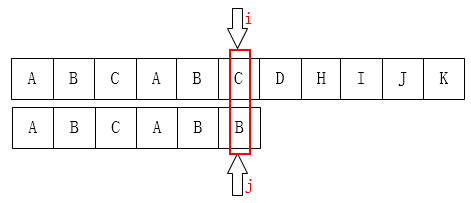
可以利用已匹配的信息，将模式指针 $j$ 移动到位置 $2$ 上，文本指针 $i$ 不变

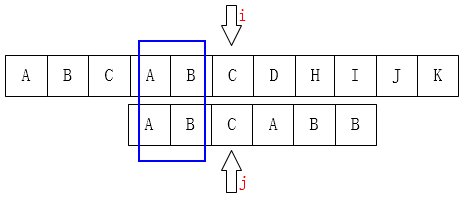
【基本原理】

通过上面两个例子可以发现，当匹配失败时，文本指针 $i$ 的位置不变，模式指针 $j$ 要移动到新的位置 $k$

这个位置 $k$ 满足：模式串前面的 $k$ 个字符与模式指针 $j$ 前的 $k$ 个字符相同

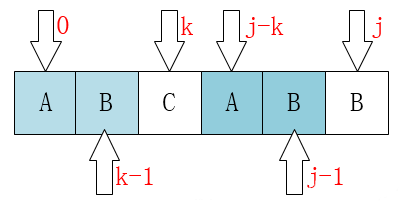
即有：

$P[0,...,k-1]=P[j-k,...,j-1]$

当出现文本串的第 $i$ 个字符与模式串的第 $j$ 个字符不匹配时，可以知道，文本串位置 $i$ 前的 $j-1$ 个字符与模式串位置 $j$ 前的 $j-1$ 个字符相同

即当 $T[i]!=P[j]$ 时，有：

$T[i-j,...,i-1]=P[0,...,j-1]$

根据 $P[0,…,k-1]=P[j-k,…,j-1]$，可得：

$T[i-k,...,i-1]=[0,...,k-1]$

因此，可直接将 $j$ 移动到 $k$，无需再比较前面的 $k$ 个字符

【next 数组】

next 数组与 PM 表

通过上面的论述，可以发现，MP 算法关键是求得 $k$

由于在模式 P 的每一个位置都可能发生不匹配，也就是说，可以采用预处理的思想，计算模式 P 中每一个位置 $j$ 所对应的 $k$，这样当出现不匹配时，直接令模式指针 $j$ 指向 $k$ 的位置

通常，使用一个数组 next[] 来保存每一个位置 $j$ 所对应的 $k$，即令 next[j]=k 来表示当 T[i]!=P[j] 时，指针 $j$ 要指向的下一个位置

模式串的部分匹配值即可满足 next 数组的要求，每当匹配失败时，就去找它前一个元素的部分匹配值，从而令模式串 P 再文本串 T 的指针 $i$ 的基础上，后移 已匹配位数-对应部分匹配值

但由于每次都要找前一个元素的部分匹配值，使用起来并不方便，因此将 PM 表整体右移一位，其有如下考虑：

第一个元素右移后的空缺用 $-1$ 填充，即：next[0]=-1，因为若第一个元素匹配失败，则需将子串整体后移一位，不需要去计算子串移动位数
最后一个元素右移溢出，将其舍去即可，因为在模式串中，最后一个元素的部分匹配值是下一个元素使用的，但显然以没有下一个元素，故直接舍去

因此，在人工求 next 数组时，可以先求出模式串 P 的 PM 表，然后令其整体右移，首位用 $-1$ 填充即可

例如，ababa 的 PM 表与 next 数组如下：

编号	0	1	2	3	4
string	a	b	a	b	a
PM	0	0	1	2	3
next	-1	0	0	1	2

next 数组的实现

根据上面的论述，在 $P[j]$ 之前已经有 $P[0,…,k-1]=P[j-k,…,j-1]$ 成立，即：

$next[j]=k$

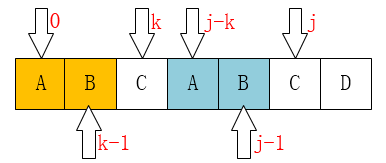
那么，当 $P[k]=P[j]$ 时，有：

$P[0,...,k-1]+P[k]=P[j-k,...,j-1]+P[j]$

合并后，有：

$P[0,...,k]=P[j-k,...,j]$

即：

$next[j+1]=k+1$

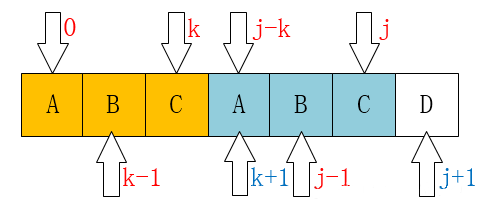
而当 $P[k]!=P[j]$ 时，根据 $P[0,…,k-1]=P[j-k,…,j-1]$，有：

$next[j]=k$

合并后，有：

$next[k]=k$

计算 next 数组的代码如下：

int next[N];
void getNext(char p[]) { //获取字符数组p的next数组
    next[0] = -1;        //初始化

    int len = strlen(p); //模式串长度
    int j = 0;           //模式指针j
    int k = -1;          //位置k

    while (j < len) {
        if (k == -1 || p[j] == p[k]) { //next[j+1]=next[j]+1
            k++; //此前有next[j]=k
            j++; //指针后移
            next[j] = k;
        } else { // k=next[k]
            k = next[k];
        }
    }
}

【MP 算法的匹配】

在求得 next 数组后，MP 算法的匹配就十分简单了，其在形式上与 BP 算法十分相似，不同之处仅在于匹配过程失配时的处理

在 MP 算法中，当出现 T[i]!=P[j] 时，文本指针 $i$ 不变，模式指针 $j$ 回退到 next[j] 的位置并重新比较

可以发现，MP 算法分为求 next 数组时间复杂度为 $O(m)$ 的预处理部分，和利用 next 数组时间复杂度为 $O(n)$ 的匹配部分，因此，其总时间复杂度为 $O(n+m)$

MP 算法的匹配过程的实现如下：

int MP(char T[], char P[]) { // MP算法
    int tLen = strlen(T);    //文本串长度
    int pLen = strlen(P);    //模式串长度

    int i = 0;  //文本串指针
    int j = 0;  //模式串指针

    getNext(P); //获取MP版本的next数组

    while (i < tLen && j < pLen) {
        if (j == -1 || T[i] == P[j]) { //当j=-1时，要移动的是i，同样j也要归零
            i++;
            j++;
        } else {
            j = next[j]; //j回到指定位置
        }
    }

    if (j == pLen) //匹配成功
        return i - j;
    return -1;
}