【概述】

二分查找（Binary Search），又称折半查找，其仅适用于有序的顺序表或数组，不适用于链表

其算法的基本思想是：将给定关键字 key 与表中中间位置的元素对应的关键字进行比较，中间结点由此将查找表分为两个子表，若相等，则查找成功，若不相等，根据关键字 key 与该中间结点关键字的比较结果来确定下一步查找哪一个子表，这样递归进行，直到查找成功或查找结束发现表中没有这样的结点

【算法分析】

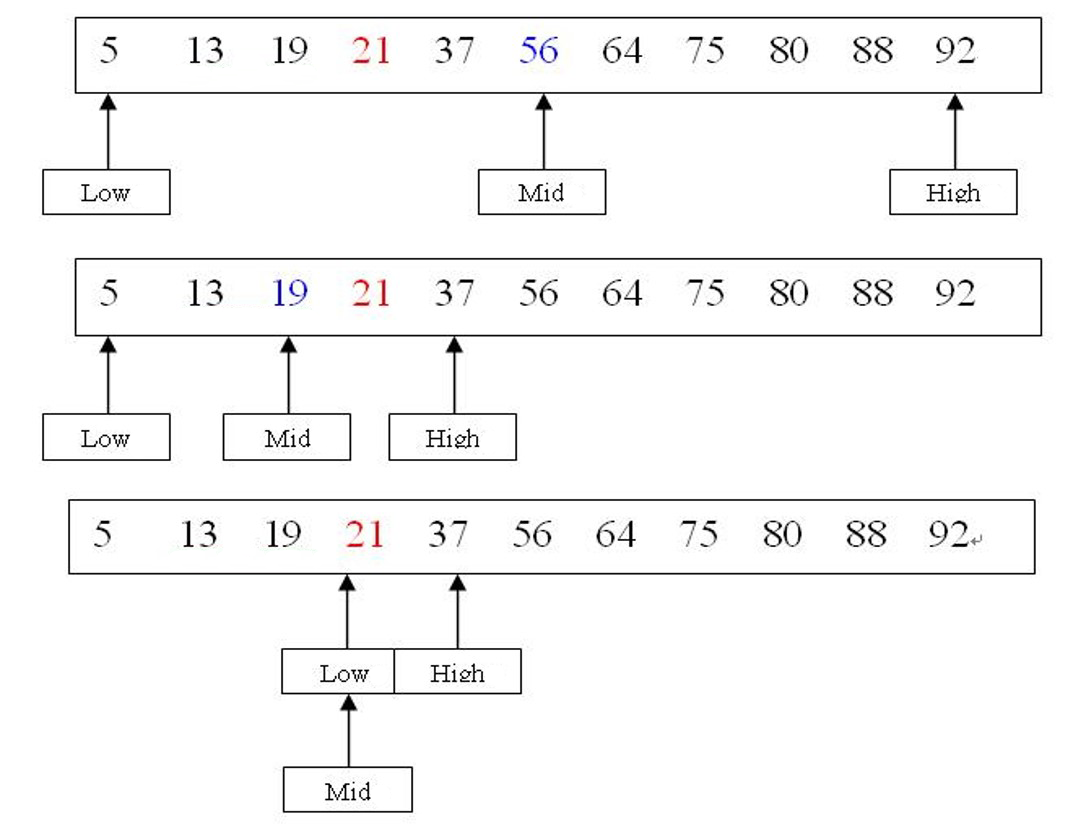
如上图所示，已知 $11$ 个元素的有序表 $\{5,13,19,21,37,56,64,75,80,88,92\}$，要查找值为 $21$ 的元素

用指针 low 指向表的下界，high 指向表的上界，mid 指向表的中间位置，有：

$mid=\lfloor \frac{low+high}{2} \rfloor$

在第一次查找时，将中间位置元素 $56$ 与 key 值 $21$ 比较，由于 $21<56$，说明若待查找元素存在，则必定在范围 $[low,mid-1]$ 内，于是：

指针 high 指向位置 $mid-1$，对应元素 $37$
指针 low 指向不变，对应元素 $5$
重新计算指针 mid，有 $mid=(1+5)/2=3$，对应元素 $19$

在第二次查找时，将中间位置元素 $19$ 与 key 值 $21$ 比较，由于 $21>19$，说明若待查找元素存在，则必定在范围 $[mid+1,high]$ 内，于是：

指针 low 指向位置 $mid+1$，对应元素 $21$
指针 high 指向不变，对应元素 $37$
重新计算指针 mid，有 $mid=(4+5)/2=4$，对应元素 $21$

在第二次查找时，即可得出查找元素 $21$ 在表中存在

【二分查找判定树】

二分查找的查找过程可用下图所示的二叉树来表示，其被称为二分查找判定树

二分查找判定树是一棵平衡二叉树，其中的每一个圆形结点代表一个记录，结点中的值为该记录的关键字值，被称为成功结点；每一个方形结点为树的叶结点，代表查找不成功的情况，被称为失败结点

同时，每个结点值均大于其左孩子结点值，均小于其右孩子结点值

若有序序列有 $n$ 个元素，那么对应的二分查找判定树有 $n$ 个成功结点和 $n+1$ 个失败叶结点

【平均查找长度】

从判定树可以看出，查找成功时的查找长度，为从根结点到目的结点的路径上的结点数，查找不成功时的查找长度，为从根结点到对应失败结点的父结点的路径上的结点数

故而，用二分查找找到给定值的比较次数，最多不会超过树的高度

在查找元素等概率的情况下，二分查找查找成功的平均查找长度为：

$\begin{align} ASL_{成功} &= \sum_{i=1}^n p_il_i \notag \\ &= \frac{1}{n}(1*1+2*2+...+h*2^{h-1}) \notag \\ &= \frac{n+1}{n} \log_2(n+1)-1 \notag \\ &\approx \log_2(n+1)-1 \end{align}$

其中，$l_i$ 为第 $i$ 层的成功结点数，$h$ 为树的高度，且元素个数为 $n$ 时，树高 $h=\lceil \log_2(n+1) \rceil$

易得二分查找的时间复杂度为：$O(\log_2n)$

在如上图所示的二分查找判定树中，在等概率情况下，有：

$\left\{ \begin{array}{rl} ASL_{成功} &=& \frac{1}{11}(1*1+2*2+3*4+4*4)=3 \\ ASL_{失败} &=& \frac{1}{12}(3*4+4*8)=\frac{11}{3} \end{array} \right.$

【实现】

查找元素

int binarySearch (int key,int a[], int n) { //在有序序列a中查找元素key的位置
    int left = 0, right = n - 1;
 
    while (left <= right) {
        int mid = (left + right) / 2; //设置中值
        if (a[mid] == key)     //查找到元素key
            return mid;
        else if (a[mid] < key) //key在右边部分
            left = mid + 1;    //调整集合下界
        else                   //key在左边部分
            right = mid - 1;   //调整集合上界
    }
    
    return -1; //若未找到key，返回-1
}

查找连续函数

除在有序表中查找指定关键字外，二分查找还可以对连续单调函数进行查找

#define EXP 1.0e-6
bool cal(int x) { //连续函数
    //根据要求进行计算
}
int binarySearch (double low, double high){ //low为区间下界，high为区间上界
    double left = low;   //设置当前查找区间上界的初值
    double right = high; //设置当前查找区间下界的初值
    
	while (right - left > EXP) { //精度小于等于1E-6时停止
        double mid = (right + left) / 2; //设置中值
        if(cal(mid) < x) //函数结果小于待查找的值
            left = mid;  //说明在右边部分，调整集合下界
        else             //函数结果大于待查找的值
            right = mid; //说明在左边部分，调整集合上界
    }
    return mid;
}