【概述】

图的搜索是指从图中某结点出发，按某种搜索方法沿着图中的边对图中的所有结点进行访问，且每个结点仅访问一次

为避免同一结点被多次访问，常通过一个标记数组 vis[] 来记录结点是否被访问过

图的搜索有两类，一类是在图上采用广度优先搜索 BFS 的思想进行搜索，另一类是在图上采用深度优先搜索 DFS 的思想进行搜索

【图的广度优先搜索】

基本过程

图的广度优先搜索的基本过程为：

从图中某个顶点 $v$ 出发，首先访问 $v$，将 $v$ 加入队列
将队首元素的未被访问过的邻接点加入队列，访问队首元素并将队首元素出队，直到队列为空
若此时图中仍有未被访问的结点，则另选图中的一个未被访问的顶点作为起始点，重复步骤 1，直到图中的所有节点均被访问过

对于无权图来说，由于 $BFS$ 总是按照距离由近到远来遍历图中的每个点，因此在每访问一个点时，令其路径长度 $+1$，即可得到无权图的单源最短路

在如下图所示的无向图中，若以 $A$ 为起点进行广度优先搜索，会按次序将 $A$ 的邻接点 $B$、$D$、$E$ 依次加入队列中，之后，令 $B$ 出队，将 $B$ 的邻接点 $C$ 加入队列中，以此类推，直到所有结点访问完毕

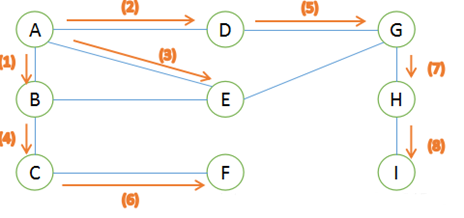
广度优先生成树

在图的广度优先遍历过程中，可以得到一棵树，这棵树即广度优先生成树

对于邻接矩阵来说，图的存储方式是唯一的，那么对应的广度优先生成树也是唯一的

对于邻接表来说，图的存储方式不唯一，那么对应的广度优先生成树不唯一

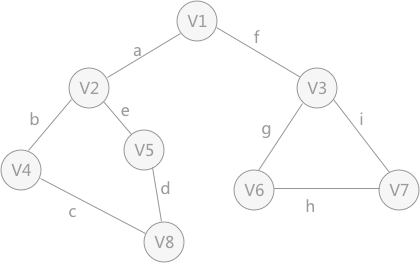
在如上图所示的无向图中，若以 $v_1$ 为起点进行广度优先搜索，得到的广度优先生成树如下图所示

时间复杂度

BFS 需要借助一个队列来完成，每个结点都要入队一次，因此实际时间复杂度取决于搜索结点的邻接点的时间复杂度

当采用邻接矩阵存储时，搜索某结点的邻接点的时间复杂度为 $O(|V|)$，那么，总时间复杂度为：

$O(|V|^2)$

当采用邻接表存储时，搜索某结点的邻接点时，每条边至少访问一次，其时间复杂度为 $O(|E|)$，那么，总时间复杂度为：

$O(|V|+|E|)$

框架

下面给出一个由 C++ 实现的采用邻接矩阵方式存储的 BFS 框架

int n,m;        //n个点m条边
char G[N][N];   //邻接矩阵
bool vis[N][N]; //标记数组
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}}; //搜索方向数组
struct Node {
    int x;
    int y;
}; //结点
void bfs(int x, int y) {
    Node start{x, y};
    vis[x][y] = true;

    queue<Node> Q;
    Q.push(start); //初始数据入队
    while (!Q.empty()) {
        Node temp = Q.front();
        Q.pop();
        if (G[temp.x][temp.y] == 'E') { //满足条件终止
            // do something
            return;
        }
        for (int i = 0; i < 4; i++) {    //朝上下左右四个方向搜索
            int nx = temp.x + dir[i][0]; //下一结点的x坐标
            int ny = temp.y + dir[i][1]; //下一结点的y坐标
            if (nx >= 1 && ny >= 1 && nx <= n && ny <= m) {
                if (!vis[nx][ny]) {
                    vis[nx][ny] = true; //标记
                    Node endd{nx, ny};
                    Q.push(endd); //元素入队
                }
            }
        }
    }
}

【图的深度优先搜索】

基本过程

图的深度优先遍历的基本过程为：

从图中某个顶点 $v_0$ 出发，首先访问 $v_0$
访问结点 $v_0$ 的第一个邻接点，以这个邻接点 $v_t$ 作为一个新节点，访问 $v_t$ 所有邻接点，直到以 $v_t$ 出发的所有节点都被访问
回溯到 $v_0$ 的下一个未被访问过的邻接点，以这个邻结点为新节点，重复步骤 2，直到图中所有与 $v_0$ 相通的所有节点都被访问
若此时图中仍有未被访问的结点，则另选图中的一个未被访问的顶点作为起始点，重复步骤 1，直到图中的所有节点均被访问

在如下图所示的无向图中，若以 $A$ 为起点进行深度优先搜索，会按 $A$、$B$、$C$、$F$ 的次序进行递归，当到达 $F$ 后，发现无法继续向下递归，开始回溯，回溯到 $B$ 时，从 $B$ 的邻接点开始向下递归，以此类推，直到所有结点访问完毕

深度优先生成树

与图的广度优先搜索类似，在图的深度优先搜索过程中，同样可以得到一棵树，这棵树即深度优先生成树

对于邻接矩阵来说，图的存储方式是唯一的，那么对应的广度优先生成树也是唯一的

对于邻接表来说，图的存储方式不唯一，那么对应的广度优先生成树不唯一

在如上图所示的无向图中，若以 $v_1$ 为起点进行广度优先搜索，得到的广度优先生成树如下图所示

时间复杂度

DFS 是一个递归的算法，需要借助一个递归工作栈来完成，因此实际时间复杂度取决于搜索结点的邻接点的时间复杂度

当采用邻接矩阵存储时，搜索某结点的邻接点时，时间复杂度为 $O(|V|)$，那么总时间复杂度为：

$O(|V|^2)$

当采用邻接表存储时，搜索某结点的邻接点时，每条边至少访问一次，时间复杂度为 $O(|E|)$，那么总时间复杂度为：

$O(|V|+|E|)$

框架

下面给出一个由 C++ 实现的采用邻接矩阵方式存储的 DFS 框架

int n,m;        //n个点m条边
char G[N][N];   //邻接矩阵
bool vis[N][N]; //标记数组
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}}; //搜索方向数组
void dfs(int x, int y) {
    for (int i = 0; i < 4; i++) { //朝上下左右四个方向搜索
        int nx = x + dir[i][0];   //下一结点的x坐标
        int ny = y + dir[i][1];   //下一结点的y坐标
        if (G[nx][ny] == 'E') {   //满足条件终止
            // do something
            return;
        }
        if (nx >= 1 && ny >= 1 && nx <= n && ny <= m){
            if (!vis[nx][ny]) {
                vis[nx][ny] = true;
                dfs(nx, ny); //向下递归
            }
        }
    }
}