Alex_McAvoy

想要成为渔夫的猎手

AOE网与关键路径

发表于 分类于 ， ，
本文字数： 6.1k 阅读时长 ≈ 6 分钟

【AOE 网】

日常生活中，一项大的工程可以看作是由若干个子工程组成的集合，这些子工程之间必定存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始

用结点表示活动，用弧表示活动间优先关系，形成的无权 DAG 图，被称为顶点活动网络

而用结点表示事件，用弧表示活动，用边权表示活动持续时间的有权 DAG 图，被称为边活动网络（Activity On Edge Network，AOE 网）

与 AOV 网相同，AOE 网同样存在如下基本概念：

  • 活动：子工程组成的集合，每个子工程即为一个活动
  • 前驱活动：有向边起点的活动称为终点的前驱活动，只有当一个活动的前驱全部都完成后，这个活动才能进行
  • 后继活动：有向边终点的活动称为起点的后继活动
  • 源点：工程开始的结点，入度为 $0$
  • 汇点：工程结束的结点，出度为 $0$

【关键路径】

AOE 网，主要用于工程管理，在 AOE 网中，有些活动是可以并行进行的，这就导致从源点到汇点的有向路径有多条，且这些路径长度不同

完成不同路径上的活动所需时间不同，只有所有路径上的活动都已完成，整个工程才算结束

关键路径被定义为从源点到汇点的具最大路径长度的路径，该路径上的活动被称为关键活动

关键活动决定了整个工程的工期，因此可以通过加快关键活动来缩短工程的工期，但不能任意缩短关键活动，当缩短到一定程度，会使得关键活动变为非关键活动

而 AOE 网中的关键活动不唯一，对于有几条关键路径的网，只提高一条关键路径上的关键活动并不能缩短整个工程的工期，只有加快包括在所有关键路径上的关键活动，才能缩短工期

此外，完成整个工程的最短时间就是关键路径的长度，即关键路径上各活动花费开销总和，这是因为关键活动若不按期完成，则整个工程的完成时间就会被延长

因此，只要找到关键路径，就能得到工程的最短完成时间

【关键路径寻找参量】

事件 $v_k$ 的最早发生时间 $ve(k)$

$ve(k)$ 是从源点 $v_1$ 开始到结点 $v_k$ 的最大路径长度，其是在保证工程顺利完成的基础上，事件最早的开始时间，其决定了所有从 $v_k$ 开始的活动能够开工的最早时间，因此称为最早发生时间

求解 $ve(k)$ 可以从源点 $ve(1)=0$ 开始

按照拓扑排序的规则，每输出一个入度为 $0$ 的顶点 $v_j$，计算它所有直接后继顶点 $v_k$ 的最早发生时间，即有：

事件 $v_k$ 的最晚发生时间 $vl(k)$

$vl(k)$ 是在保证工程顺利完成的基础上，事件 $v_k$ 最迟的开始时间，因此被称为最晚发生时间

求解 $vl(k)$ 可以从汇点 $vl(n)=ve(n)$ 开始

按照逆拓扑排序的规则，每输出一个出度为 $0$ 的顶点 $v_j$，计算它所有直接前驱顶点 $v_k$ 的最晚发生时间，即有：

活动 $a_i$ 的最早开始时间 $ee(i)$

$ee(i)$ 是在保证工程顺利完成的基础上，活动 $a_i$ 最早的必须开始时间，因此被称为最早开始时间

根据 AOE 网的性质，只有事件 $v_k$ 发生后，活动 $a_i$ 才能开始，那么若活动 $a_i$ 由 $< v_k, v_j >$ 表示，活动 $a_i$ 的最早开始时间等于事件 $v_k$ 的最早发生时间，即：

活动 $a_i$ 的最晚开始时间 $el(i)$

$el(i)$ 是在保证工程顺利完成的基础上，活动 $a_i$ 最迟的必须开始时间，因此被称为最晚开始时间

若活动 $a_i$ 由弧 $< v_k, v_j >$ 表示，则 $a_i$ 的最晚开始时间要保证事件 $v_j$ 的最迟发生时间不拖后，即：

活动 $a_i$ 的松弛时间 $d(i)$

$d(i)$ 是指活动完成的时间余量，即在不增加完成整个工程所需时间的情况下，活动 $a_i$ 可以拖延的时间，其值为 $a_i$ 的最晚开始时间 $el(i)$ 与最早开始时间 $ee(i)$ 的差值，即：

若一个活动松弛时间为 $0$，那么说明该活动必须按期完成，否则会影响整个工程的进度

也就是说，若满足 $el(i)-ee(i)=0$，即满足 $el(i)=ee(i)$ 时，活动 $a_i$ 是关键活动

【关键路径的求解】

关键路径的求解算法如下：

1）求结点的最早发生时间 $ve(i)$

从源点出发，令 $ve(1)=0$，按拓扑序列，求解每个顶点 $i$ 的最早发生时间 $ve(i)$，即：

2）求结点的最晚发生时间 $vl(i)$

从汇点出发，令 $vl(n)=ve(n)$，按逆拓扑序列，求解每个顶点 $i$ 的最晚发生时间 $vl(i)$，即：

3）求弧的最早开始时间 $ee(i)$

根据各顶点 $i$ 的最早发生时间 $ve(i)$ 求所有弧 $< v_k, v_j >$ 的最早开始时间 $ee(i)$，即：

4）求弧的最晚开始时间 $el(i)$

根据各顶点 $i$ 的最晚发生时间 $vl(i)$ 求所有弧 $< v_k, v_j >$ 的最晚开始时间 $el(i)$，即：

4）求弧的松弛时间 $d(i)$

计算所有弧的松弛时间 $d(i)$，找出所有 $d(i)=0$ 的弧，其构成一条关键路径，即：

【实例】

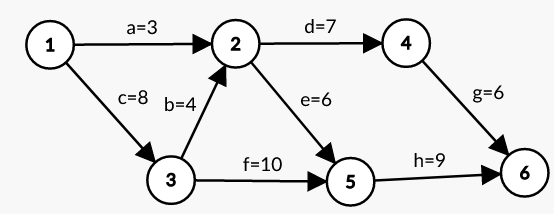
在上图所示的 AOE 网中，从源点事件 $1$ 和汇点事件 $6$，进行拓扑排序，可以得到一个拓扑序列为 $132456$，由此，事件最早发生时间 $ve(i)$ 与事件最晚发生时间 $vl(i)$ 如下表：

事件 $i$ $1$ $3$ $2$ $4$ $5$ $6$
$ve(i)$ $0$ $8$ $12$ $19$ $18$ $27$
$vl(i)$ $0$ $8$ $12$ $21$ $18$ $27$

进一步，由于活动 $i$ 是由弧 $< v_k, v_j >$ 表示，那么，活动 $a$ 到活动 $h$ 的最早开始时间 $ee(i)$ 与最晚开始时间 $el(i)$ 如下表：

活动 $i$ $a$ $b$ $c$ $d$ $e$ $f$ $g$ $h$
对应弧 $< v_k, v_j >$ $< 1,2 >$ $< 3,2 >$ $< 1,3 >$ $< 2,4 >$ $< 2,5 >$ $< 3,5 >$ $< 4,6 >$ $< 5,6 >$
$ve(v_k)$ $0$ $8$ $0$ $12$ $12$ $8$ $19$ $18$
$vl(v_j)$ $12$ $12$ $8$ $19$ $18$ $18$ $27$ $27$
弧长 $3$ $4$ $8$ $7$ $6$ $10$ $6$ $9$
$ee(i)$ $0$ $8$ $0$ $12$ $12$ $8$ $19$ $18$
$el(i)$ $12-3=9$ $12-4=8$ $8-8=0$ $21-7=14$ $18-6=12$ $18-10=8$ $27-6=21$ $27-9=18$

故活动的松弛时间 $d(i)$ 如下表：

活动 $i$ $a$ $b$ $c$ $d$ $e$ $f$ $g$ $h$
$ee(i)$ $0$ $8$ $0$ $12$ $12$ $8$ $19$ $18$
$el(i)$ $9$ $8$ $0$ $14$ $12$ $8$ $21$ $18$
$d(i)$ $9$ $0$ $0$ $2$ $0$ $0$ $2$ $0$

可知，活动 $b$、$c$、$e$、$f$、$h$ 为关键活动，他们构成的路径 $cbeh$、$cbfh$ 为两条关键路径

在这两条关键路径中，活动 $c$、$b$、$h$ 在所有的关键路径中，因此，加快这三个活动的进度，能够缩短工期

【实现】

输出关键路径

根据关键路径的定义，依次求出 $ve$、$vl$、$ee$、$el$，然后比较 $ee$、$el$ 进行输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
int n,m;
int G[N][N];  //邻接矩阵
bool vis[N];  //访问数组
int in[N];    //入度
int ve[N];    //事件vk的最早发生时间
int vl[N];    //事件vk的最晚发生时间
int ee[N];    //活动ai的最早开始时间
int el[N];    //活动ai的最晚开始时间
int Stack[N]; //栈
struct Edge {
    int x, y;
    int dis;
    Edge() {}
    Edge (int x, int y, int dis): x(x), y(y), dis(dis){}
} edge[N];
void getVe() { //求ve
    int cnt = 0;
    for (int i = 1; i <= n; i++) { //从源点开始，求每个结点i的ve
        int k = -1;
        for (int j = 1; j <= n; j++) { //按拓扑序列寻找入度为0的点
            if (in[j] == 0) { //入度为0，进栈
                Stack[++cnt] = j;
                k=j;
                in[j]=-1;
                break;
            }
        }
        for (int j = 1; j <= n; j++) { //计算ve
            if(G[k][j] != INF) {
                ve[j] = max(ve[j], ve[k] + G[k][j]);
                in[j]--;
            }
        }
    }
}
void getVl() { //求vl
    memset(vl, INF, sizeof(vl));
    vl[Stack[n]] = ve[Stack[n]];
    for (int i = n; i >= 1; i--) { //从汇点开始，求每个结点i的vl
        for (int j = 1; j <= n; j++) //计算vl
            if (G[Stack[i]][j] != INF) 
                vl[Stack[i]] = min(vl[j] - G[Stack[i]][j] , vl[Stack[i]]);
    }
}
void getEe() { //求ee
    for (int i=1; i<=m; i++)
        ee[i] = ve[edge[i].x];
}
void getEl() { //求el
    for (int i = 1; i <= m; i++)
        el[i] = vl[edge[i].y] - edge[i].dis;
}
 
void printEdge() { //以边输出
    for (int i = 1; i <= m; i++)
        if (ee[i] == el[i]) //松弛时间为0的关键活动
            printf("<%d,%d>:%d\n", edge[i].x, edge[i].y, edge[i].dis);
}
void printNode(){ //以点输出
    priority_queue<int, vector<int>, greater<int> > Q;
    memset(vis, false, sizeof(vis));
    
    for (int i = 1; i <= m; i++) {
        if (ee[i] == el[i]) { //松弛时间为0的关键活动
            int x = edge[i].x;
            int y = edge[i].y;
            if (!vis[x]) {
                Q.push(x);
                vis[x] = true;
            }
            if (!vis[y]) {
                Q.push(y);
                vis[y] = true;
            }
        }
    }
    while (!Q.empty()) {
        int temp = Q.top();
        Q.pop();
        printf("v%d ", temp);
    }
}
int main() {
    memset(G,INF,sizeof(G));
 
    scanf("%d%d",&n, &m);
    for(int i = 1; i <= m; i++) {
        int x, y, dis;
        scanf("%d%d%d",&x, &y, &dis);
        edge[i].x = x;
        edge[i].y = y;
        edge[i].dis = dis;
 
        G[x][y] = dis;
        in[y]++;
    }
 
    getVe();
    getVl();
    getEe();
    getEl();
 
    printf("以边输出：\n");
    printEdge();
    printf("以点输出：\n");
    printNode();
 
    return 0;
}

求关键路径长度

由于关键路径是具有最大路径长度的路径，因此直接求有向图的最长路即为关键路径的长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
struct Node {
    int to, dis;
    Node(){}
    Node(int to, int dis): to(to), dis(dis){}
};
int n, m;
int in[N];
vector<Node> G[N];
int dis[N];
void getPath() {
    queue<int> Q;
    for (int i = 0; i < n; i++) {
        if (in[i] == 0) {
            Q.push(i);
            dis[i]++;
        }
    }
 
    while (!Q.empty()) {
        int x = Q.front();
        Q.pop();
        
        for(int i = 0; i < G[x].size(); i++) {
            int y = G[x][i].to;
            int diss = G[x][i].dis;
            dis[y] = max(dis[y], dis[x] + diss);
 
            if (--in[y] == 0)
                Q.push(y);
        }
    }
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++) {
        int x, y, dis;
        scanf("%d%d%d", &x, &y, &dis);
        G[x].push_back(Node(y, dis));
        in[y]++;
    }
 
    getPath();
    int res = -INF;
    for(int i = 0; i < n; i++)
        res = max(res, dis[i]);
    printf("%d\n",res);

    return 0;
}
感谢您对我的支持，让我继续努力分享有用的技术与知识点！