二叉树的存储结构

【顺序结构】

由于树与二叉树的性质，顺序存储存储完全二叉树、满二叉树较为合适，其利用一组地址连续的存储单元，自上而下，自左到右存储完全二叉树上的结点元素，即将 $i$ 号结点存储在数组下标 $i-1$ 的分量中

而对于一般的二叉树，为了让数组下标能反应二叉树结点中的逻辑关系，只能添加不存在的空结点，以让每个结点与完全二叉树上的结点对照，再存储到相应的数组分量中

对于给定编号为 $i$ 的结点，其左孩子为 $2i$，右孩子为 $2i+1$，父结点为 $\left\lfloor \frac{i}{2} \right\rfloor$

struct BiTNode {
    int data;     //数据域
    bool isEmpty; //结点是否为空
} tree[N];

在最坏情况下，高度为 $h$ 的只有 $h$ 个结点的斜树要占据 $2^h-1$ 个存储单元，这极大的浪费了存储空间

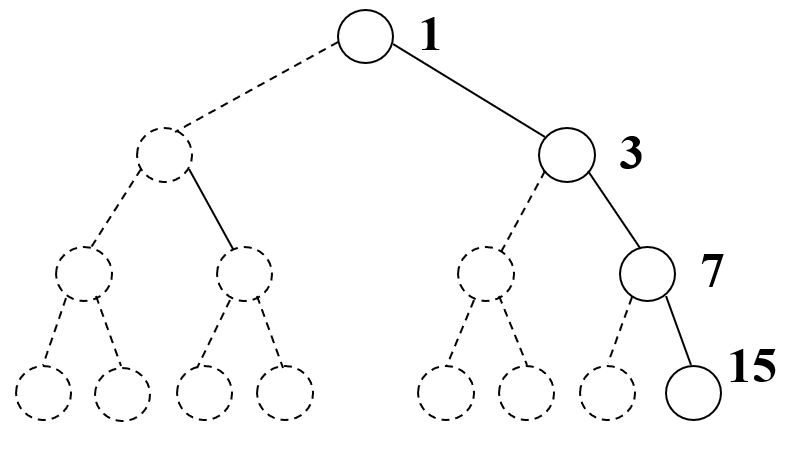
因此，二叉树的顺序存储结构一般仅用于存储完全二叉树

【链式结构】

由于顺序存储的空间利用率低，因此二叉树一般采用链式存储结构，即用链表结点存储二叉树中的结点

二叉链表

每个存储结点包含一个数据域 data，一个指向其左孩子的左指针lchild，一个指向其右孩子的右指针rchild

typedef struct BiTNode {    //二叉链表
    int data;               //数据域
    struct BiTNode *lchild; //左指针
    struct BiTNode *rchild; //右指针
} BiTNode, *BiTree;
bool initBiTree(BiTree &root) { //初始化
    root = NULL;                //空树
    return true;
}

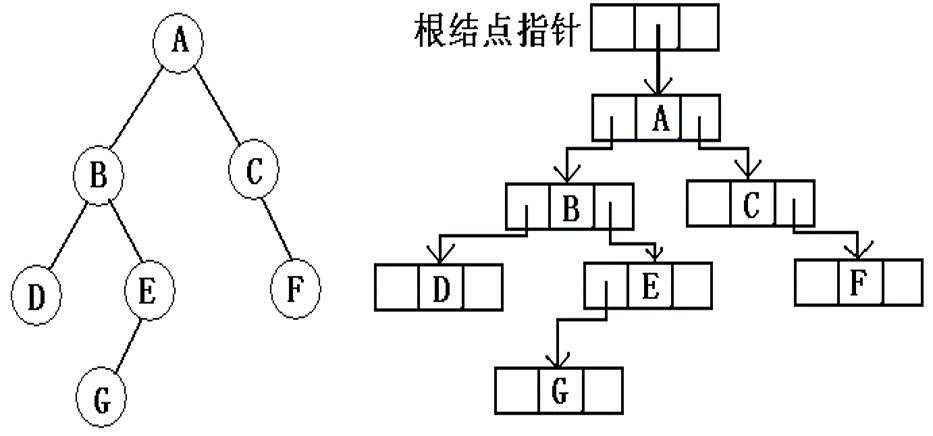
可以发现，$n$ 个结点的二叉链表共有 $n+1$ 个空链域，这无疑浪费了空间，在二叉链表的基础上，后来又有了线索链表，通过线索链表表示的二叉树，一般称为线索二叉树

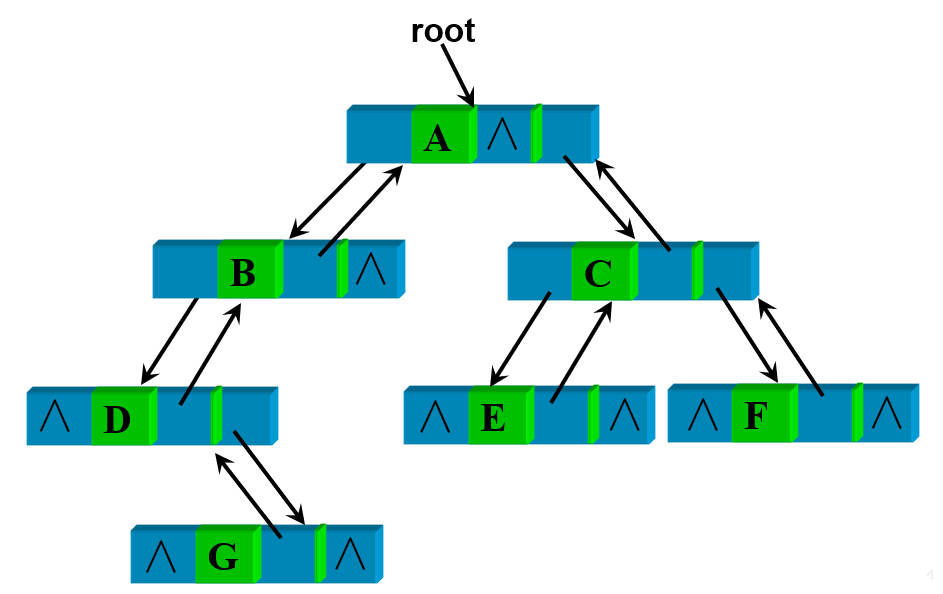
三叉链表

在二叉链表的存储方式下，从某结点出发可以直接访问到它的孩子结点，但要找到某个结点的父结点需要从根结点开始搜索，最坏情况下，需要遍历整个二叉链表

而三叉链表，在二叉链表的基础上加了一个指向父结点的指针域 parent，使得即便于查找孩子结点，又便于查找父结点，但相对二叉链表而言，加大了空间开销

typedef struct BiTNode {    //三叉链表
    int data;               //数据域
    struct BiTNode *lchild; //左指针
    struct BiTNode *rchild; //右指针
    struct BiTNode *parent; //父指针
} BiTNode, *BiTree;
bool initBiTree(BiTree &root) { //初始化
    root = NULL;                //空树
    return true;
}