二叉树的线索化

【线索化】

对二叉树以某种次序遍历使其变为线索二叉树的过程称为线索化，依据二叉树遍历次序的不同，分为前序、中序、后序三种线索二叉树

线索化的核心是建立线索，之后无论是何种形式的线索二叉树，只要在其前、中、序遍历递归过程中，更改线索建立的位置即可

在建立线索时，需要一个前驱指针 pre，用于指向当前节点 p 的前驱结点

• 若当前结点 p 没有左孩子：让 p 的左孩子指针指向当前结点的前驱 pre ，以建立前驱关系
• 若前驱结点 pre 非空，且没有右孩子：让 pre 的右孩子指针指向当前结点 p，以建立后继关系

同时，在每次完成线索建立后，令 pre 指向 p，以保持 pre 总是指向当前结点的前驱

typedef struct ThNode {    //线索链表
    int data;              //数据域
    struct ThNode *lchild; //左指针
    struct ThNode *rchild; //右指针
    int ltag, rtag;        //标志位
} ThNode, *ThTree;

void buildThread(ThNode *p, ThNode *&pre) { //建立线索
    if (p->lchild == NULL) { //当前结点p没有左孩子
        p->lchild = pre;     //p的左孩子指针指向p的前驱pre
        p->ltag = 1;         //修改标志位
    }

    if (pre != NULL) {             //前驱结点pre存在
        if (pre->rchild == NULL) { //前驱结点pre没有右孩子
            pre->rchild = p;       // pre的右孩子指向当前结点p
            pre->rtag = 1;         //修改标志位
        }
        pre = p; //保持pre指向p的前驱
    }
}

【中序线索二叉树】

对于中序线索二叉树来说，其按照中序遍历顺序，先访问左子树，再访问根结点，最后再访问右子树

void inThread(ThTree p, ThNode *&pre) { //中序线索化
    inThread(p->lchild, pre); //递归左子树线索化
    buildThread(p, pre);      //当前结点线索化
    inThread(p->rchild, pre); //递归右子树线索化
}
void createInThreadTree(ThTree root) { //建立中序线索二叉树
    if (root == NULL)
        return;

    ThTree pre = NULL;       //当前结点p的前驱结点pre
    inThread(root, pre);     //中序线索化
    if (pre->rchild == NULL) //处理遍历的最后一个结点
        pre->rtag = 1;
}

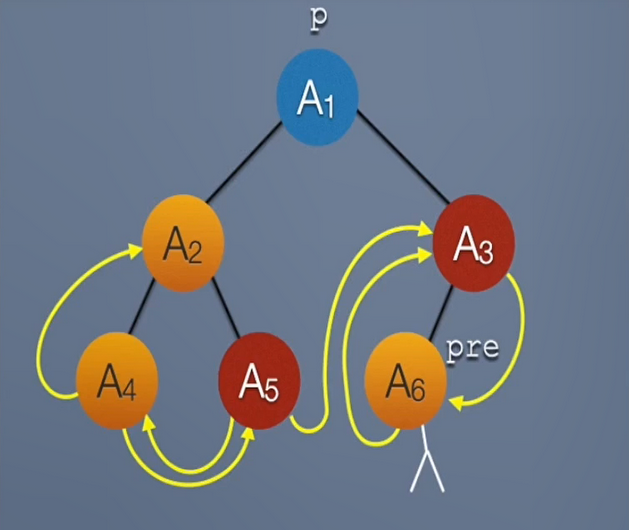
【前序线索二叉树】

对于前序线索二叉树来说，其按照前序遍历顺序，先访问根结点，再访问左子树，最后再访问右子树

在线索化过程时，由于进入递归函数后会先进行线索化，因此，这相较于中序线索二叉树来说，可能导致 pre 出现绕圈问题

为避免可能出现的绕圈，要加一个判断，即当左孩子指针 lchild 不是前驱线索时，才进行左子树线索化

void preThread(ThTree p, ThNode *&pre) { //前序线索化
    buildThread(p, pre);                 //当前结点线索化
    if (p->ltag == 0)                    // lchild不是前驱线索
        preThread(p->lchild, pre);       //递归左子树线索化
    preThread(p->rchild, pre);           //递归右子树线索化
}
void createPreThreadTree(ThTree root) { //建立前序线索二叉树
    if (root == NULL)
        return;

    ThTree pre = NULL;       //当前结点p的前驱结点pre
    preThread(root, pre);    //前序线索化
    if (pre->rchild == NULL) //处理遍历的最后一个结点
        pre->rtag = 1;
}

【后序线索二叉树】

对于后序线索二叉树来说，其按照后序遍历顺序，先访问左子树，再访问右子树，最后再访问根结点

void postThread(ThTree p, ThNode *&pre) { //后序线索化
    postThread(p->lchild, pre);           //递归左子树线索化
    postThread(p->rchild, pre);           //递归右子树线索化
    buildThread(p, pre);                  //当前结点线索化
}
void createPostThreadTree(ThTree root) { //建立后序线索二叉树
    if (root == NULL)
        return;
    ThTree pre = NULL;       //当前结点p的前驱结点pre
    postThread(root, pre);   //后序线索化
    if (pre->rchild == NULL) //处理遍历的最后一个结点
        pre->rtag = 1;
}