顺序队列

【概述】

顺序队列是采取顺序方式存储的队列，利用一组地址连续的存储单元自队首到队尾存放数据元素，并通过队首指针来指示当前队首元素位置，通过队尾指针来指示当前队尾元素的下一位置

对于存储空间的分配，若采用静态分配方式，一经分配不可修改，若采用动态分配方式，分配后在 $O(n)$ 的时间复杂度内可以更改

顺序队列的实现类如下：

#define N 50 + 5 //申请空间个数
template <typename T> 
class SeqQueue {
  public:
    SeqQueue();           //初始化队
    int getLen();         //求队长
    bool empty();         //判空
    bool full();          //判满
    bool pop(T &elem);    //出队
    bool push(T elem);    //入队
    bool getTop(T &elem); //取队首
    void print();         //输出
  private:
    T data[N];            //队列空间
    int head;             //队首指针
    int tail;             //队尾指针
};

【初始化】

初始时，队列为空队列，此时队头指针 head 与队尾指针 tail 均设为 $0$

template <typename T> 
SeqQueue<T>::SeqQueue() { //初始化队列
    head = 0;
    tail = 0;
}

【求队长】

队列的队尾指针 tail 与队首指针 head 的差值，即为队列的队长

template <typename T> 
int SeqQueue<T>::getLen() { //求队长
    return tail-head;
}

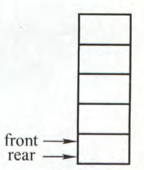
【判空】

由于 tail 指向队尾元素的下一位置，即接下来要插入的位置，因此在判空时，只需判断队尾指针与队头指针是否相同即可

template <typename T> 
bool SeqQueue<T>::empty() { //判空
    if (head == tail)
        return true;
    return false;
}

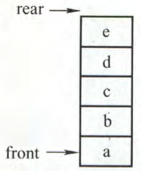
【判满】

当队尾指针 tail 的值为申请空间个数时，说明空间已满

template <typename T> 
bool SeqQueue<T>::full() { //判满
    if (tail == N)
        return true;
    return false;
}

---

顺序队列中存在假溢出问题，即当队列经过一定的入队出队操作后，队列的低端存在一部分的空闲空间，而队列的高端空间已被用尽，此时尽管数组中还有空间，但由于队列的入队操作只会插入到数组尾部，此时继续入队会发生假溢出

【出队】

在出队时，取队首指针 head 指向的元素，之后令队首指针后移一位，即 head++

template <typename T> 
bool SeqQueue<T>::pop(T &elem) { //出队
    if (empty()) //下溢判断
        return false;
    elem = data[head++];
    return true;
}

【入队】

在入队时，将元素存入队尾指针 tail 指向的位置，之后令队尾指针后移一位，即 tail++

template <typename T> 
bool SeqQueue<T>::push(T elem) { //入队
    if (full()) //上溢判断
        return false;
    data[tail++] = elem;
    return true;
}

【取队首】

在取队首元素时，先进行下溢判断，然后直接取队首指针 head 指向的元素即可

template <typename T> 
bool SeqQueue<T>::getTop(T &elem) { //取队首
    if (empty()) //下溢判断
        return false;
    elem = data[head];
    return true;
}

【输出】

在输出时，从队首开始，将队列中所有元素依次出队，进行输出即可

template <typename T> 
void SeqQueue<T>::print() { //输出
    int elem;
    while (!empty()) { //将所有元素依次出队进行输出
        pop(elem);
        cout << elem << " ";
    }
    cout << endl;
}