【单链表】

概述

线性表的链式存储方式称为链表，其通过一组任意存储单元来存储线性表中的数据元素，最基本一种链接方式构成的链表称为单链表

为了建立数据元素间的线性关系，对于每个链表结点，除了存放数据元素（数据域）外，还要存储指向下一结点的指针（指针域）

这就使得不再要求大片连续的空间来存储数据，可以利用指针来将不连续的空间建立链接关系，进一步可以对空间进行扩充

此外，由于指针的特性，在单链表中查找某个元素时，要从表头开始遍历，这被称为非随机存取

头指针与头结点

为了标识单链表，引入头指针的概念，其始终指向单链表的第一个结点

同时，在单链表第一个结点前附加一个结点，其数据域一般存储表长等信息，指针域指向单链表第一个结点，这个附加的结点被称为头结点

头结点引用的目的是为了方便编程，将空表与非空表的操作统一，无须特殊处理：

头结点指针域指向单链表第一个结点，使得第一个结点的操作与其他结点操作一致
无论单链表是否为空，头指针都指向头结点的指针

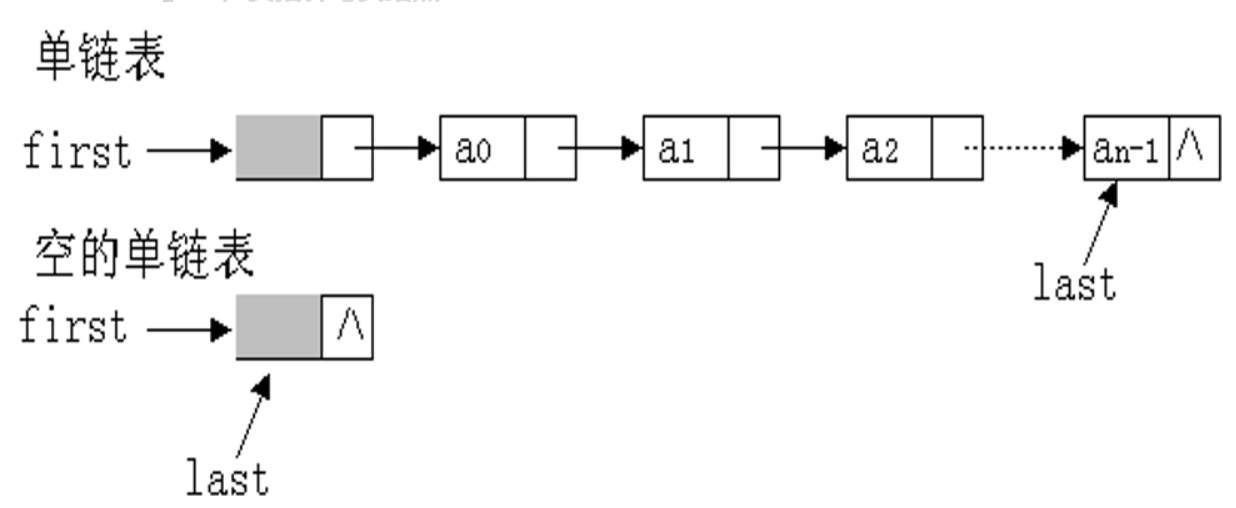
在带有头结点时，头指针会指向头结点（第 $0$ 个结点），头结点指向链表第 $1$ 个结点；在不带头结点时，头指针直接指向单链表的第 $1$ 个结点

单链表的实现类如下：

template <typename T> 
struct LNode {       //单链表结点
    T data;          //数据域
    LNode<T> *next;  //指针域
};
template <typename T> 
class LinkList {
  public:
    LinkList();                                    //无参构造函数，初始化表
    LinkList(T data[], int len);                   //有参构造函数，链表建立
    ~LinkList();                                   //析构函数，链表销毁
    int getLen();                                  //求表长
    bool empty();                                  //判空
    void print();                                  //输出
    LNode<T> *getNodeByValue(T elem);              //按值查找
    LNode<T> *getNodeByLocate(int pos);            //按位查找
    bool insertNextNode(LNode<T> *p, T elem);      //后插，用于按位插入
    bool insertPreNode(LNode<T> *p, T elem);       //前插，用于按位插入
    bool insertNode(int pos, T elem);              //按位插入
    bool deleteNodeByLocate(LNode<T> *p, T &elem); //删除指定结点p
    bool deleteNodeByElem(T elem);                 //删除所有值为elem的结点
    void headInsert(T data[], int len);            //头插法
    void tailInsert(T data[], int len);            //尾插法
  private:
    LNode<T> *first;                               //头指针
};

【初始化表与销毁表】

初始化与单链表的建立

对于单链表 L 来说，在初始化完毕后，即可对于给定的数据序列 data[] 来建立单链表，建立单链表有两种方式，一种是头插法，另一种是尾插法

对于带头结点的单链表 L，在进行初始化时，需要为头指针 first 建立一个头结点，并使头结点的指向为 NULL

template <typename T> 
LinkList<T>::LinkList() {                         //无参构造函数，初始化
    first = (LNode<T> *)malloc(sizeof(LNode<T>)); //分配一头结点
    first->next = NULL;                           //空表
}
template <typename T>
LinkList<T>::LinkList(T data[], int len) {        //有参构造函数，链表建立
    first = (LNode<T> *)malloc(sizeof(LNode<T>)); //分配一头结点
    first->next = NULL;                           //空表

    this->headInsert(data, len);    //头插法
    // this->tailInsert(data, len); //尾插法
}

对于不带头结点的单链表 L，在进行初始化时，令头指针 first 指向为 NULL 即可

template <typename T> 
LinkList<T>::LinkList() {  //无参构造函数，初始化
    first = NULL;          //空表
}
template <typename T>
LinkList<T>::LinkList(T data[], int len) {  //有参构造函数，链表建立
    first = NULL;                           //空表

    this->headInsert(data, len);            //头插法
    // this->tailInsert(data, len);         //尾插法
}

单链表的销毁

对于单链表 L 来说，若要将其销毁，需要从头指针 first 指向的结点开始，逐个将链表中结点的存储空间释放

template <typename T> 
LinkList<T>::~LinkList() {   //析构函数，链表销毁
    while (first != NULL) {
        LNode<T> *p = first; //暂存要被释放的结点
        first = first->next; //头指针指向要被释放的结点的下一个结点
        free(p);             //释放空间
    }
}

【基本操作】

求表长

对于带头结点的单链表 L，若想求其长度，只需从头结点开始枚举，依次判断下一结点是否为 NULL，同时，每枚举一个结点令长度加一，直到当前结点所指向的下一个结点为 NULL 为止

template <typename T> 
int LinkList<T>::getLen() {   //求表长
    int len = 0;
    LNode<T> *p = first;      //为保证头指针指向不变，建立临时指针变量进行枚举
    while (p->next != NULL) { //判断下一结点是否为 NULL
        p = p->next;
        len++;
    }
    return len;
}

对于不带头结点的单链表 L，若想求其长度，只需从头指针指向的第一个结点开始枚举，依次判断当前结点是否为 NULL，同时，每枚举一个结点令长度加一，直到当前结点所指向的下一个结点为 NULL 为止

template <typename T> 
int LinkList<T>::getLen() { //求表长
    int len = 0;
    LNode<T> *p = first;    //为保证头指针指向不变，建立临时指针变量进行枚举
    while (p != NULL) {     //判断当前结点是否为 NULL
        p = p->next;
        len++;
    }
    return len;
}

判空

对于带头结点的单链表 L，若想判断其是否为空，只需判断 L 的头指针指向的头结点是否指向 NULL 即可

template <typename T> 
bool LinkList<T>::empty() { //判空
    if (first->next == NULL)
        return true;
    return false;
}

对于不带头结点的单链表 L，若想判断其是否为空，只需判断 L 的头指针的指向是否为 NULL 即可

template <typename T> 
bool LinkList<T>::empty() { //判空
    if (first == NULL)
        return true;
    return false;
}

输出

对于带头结点的单链表 L，若将其输出，只需从头结点指向的第一个节点开始遍历，只要结点不为空，就输出结点的数据域

template <typename T> 
void LinkList<T>::print() {     //输出
    LNode<T> *p = first->next;  //指向第1个结点
    while (p != NULL) {
        cout << p->data << " ";
        p = p->next;
    }
    cout << endl;
}

对于不带头结点的单链表 L，若将其输出，只需从头指针指向的第一个节点开始遍历，只要结点不为空，就输出结点的数据域

template <typename T> 
void LinkList<T>::print() { //输出
    LNode<T> *p = first;    //指向第1个结点
    while (p != NULL) {
        cout << p->data << " ";
        p = p->next;
    }
    cout << endl;
}

【查找】

按值查找

按值查找，即获取 L 中与给定参数值 elem 相同的结点，若查找失败，则返回 NULL，若查找成功，则返回该结点，因此，在调用该方法时，需要进行判断是否返回值为 NULL

对于带头结点的单链表 L，只需从头结点开始遍历，判断当前数据域是否为 elem

template <typename T>
LNode<T> *LinkList<T>::getNodeByValue(T elem) { //按值查找
    LNode<T> *p = first->next;                  //从头结点开始
    while (p != NULL && p->data != elem)
        p = p->next;
    return p;
}

对于不带头结点的单链表 L，只需从头指针开始遍历，判断当前数据域是否为 elem

template <typename T>
LNode<T> *LinkList<T>::getNodeByValue(T elem) { //按值查找
    LNode<T> *p = first;                        //从头指针开始
    while (p != NULL && p->data != elem)
        p = p->next;
    return p;
}

按位查找

按位置查找，即获取 L 中第 pos 个结点，在查找前需要进行越界判断，若查找位置异常，则返回 NULL，若查找位置正常，则返回该结点，因此，在调用该方法时，需要进行判断是否返回值为 NULL

对于带头结点的单链表 L，之后建立一个从 $0$ 开始的累加器，记录当前指针指向的是第几个结点，当遍历到第 pos 个结点时，返回指针所指向的当前结点即可

template <typename T>
LNode<T> *LinkList<T>::getNodeByLocate(int pos) { //按位查找
    if (pos < 0)                                  //越界判断
        return NULL;
    if (pos == 0)                                 //返回头结点
        return first;

    LNode<T> *p;     //扫描器，当前扫描到的工作结点
    p = first;       //扫描器从头结点开始，头结点是第0个结点
    int now_pos = 0; //累加器，记录p指向的第几个结点

    while (p != NULL && now_pos < pos) { //查找第pos个结点
        p = p->next;
        now_pos++;
    }
    return p;
}

对于不带头结点的单链表 L，之后建立一个从 $1$ 开始的累加器，记录当前指针指向的是第几个结点，当遍历到第 pos 个结点时，返回指针所指向的当前结点即可

template <typename T>
LNode<T> *LinkList<T>::getNodeByLocate(int pos) { //按位查找
    if (pos <= 0)                                 //越界判断
        return NULL;

    LNode<T> *p;     //扫描器，当前扫描到的工作结点
    p = first;       //扫描器从头指针开始，头指针指向的是第0个结点
    int now_pos = 1; //累加器，记录p指向的第几个结点

    while (p != NULL && now_pos < pos) { //查找第pos个结点
        p = p->next;
        now_pos++;
    }
    return p;
}

【插入】

后插

后插，是指在给定 p 结点后插入元素 elem，一般用于按位插入，不单独使用

template <typename T>
bool LinkList<T>::insertNextNode(LNode<T> *p, T elem) { //后插，用于按位插入
    if (p == NULL)
        return false;

    LNode<T> *s = (LNode<T> *)malloc(sizeof(LNode<T>)); //申请新结点
    s->data = elem;
    s->next = p->next;
    //将s链接至p后
    p->next = s;

    return true;
}

前插

前插，是指在给定 p 结点前插入元素 elem，由于指针机制是后向机制，若采用循环遍历的方式找到前驱结点进行前插，时间复杂度为 $O(n)$，而采用以下交换数据的方式，时间复杂度仅为 $O(1)$

前插与后插一样，一般用于按位插入，不单独使用

template <typename T>
bool LinkList<T>::insertPreNode(LNode<T> *p, T elem) { //前插，用于按位插入
    if (p == NULL)
        return false;

    LNode<T> *s = (LNode<T> *)malloc(sizeof(LNode<T>)); //申请新结点

    //将新结点s链接到工作结点p后
    s->next = p->next;
    p->next = s;

    //交换数据
    s->data = p->data; //将p结点的数据存入s结点
    p->data = elem;    //将元素elem存入p结点
    
    return true;
}

按位插入

按位置插入，即在 L 中第 pos 个结点插入元素 elem，在插入前需要进行越界判断，在插入时，可以找到第 pos-1 个结点进行后插，也可以找到第 i 个结点进行前插，但无论使用后插还是前插，都需要注意判断插入位置是否异常

对于带头结点的单链表 L，由于头结点的存在，使得操作统一，因此直接进行插入即可

template <typename T> 
bool LinkList<T>::insertNode(int pos, T elem) { //按位插入
    if (pos < 1)                                //越界判断
        return false;

    //后插
    LNode<T> *p = getNodeByLocate(pos - 1);     //找到第pos-1个位置
    if (p == NULL)                              //插入位置异常
        return false;
    return insertNextNode(p, elem);             //在pos-1个位置后插入元素

    //前插
    // LNode<T> *p = getNodeByLocate(pos);      //找到第pos个位置
    // if (p == NULL)                           //插入位置异常
    //     return false;
    // return insertPreNode(p, elem);           //在pos个位置前插入元素
}

对于不带头结点的单链表 L，在插入第一个位置时，需要改变头指针 ，令其指向新的结点，其余位置则与带头结点的单链表操作相同

template <typename T>
bool LinkList<T>::insertNode(int pos, T elem) { //按位插入
    if (pos < 1)                                //越界判断
        return false;
    
    //第1个结点
    if (i == 1) {                               
        LNode<T> *s = (LNode<T> *)malloc(sizeof(LNode<T>));
        s->data = elem;
        s->next = first; //新结点指向头指针所指向的第一个结点
        first = s;       //头指针指向新结点
        return true;
    }
    
    //后插
    LNode<T> *p = getNodeByLocate(pos - 1);     //找到第pos-1个位置
    if (p == NULL)                              //插入位置异常
        return false;
    return insertNextNode(p, elem);             //在pos-1个位置后插入元素

    //前插
    // LNode<T> *p = getNodeByLocate(pos);      //找到第pos个位置
    // if (p == NULL)                           //插入位置异常
    //     return false;
    // return insertPreNode(p, elem);           //在pos个位置前插入元素
}

【删除】

删除指定结点

在按值查找、按位查找寻找到某一指定结点 p 后，要删除该结点并返回该结点的数据域 elem，方法如下：

若删除的是非最后结点，只需将要删除的结点 p 之后的结点 s 的数据存入 p，然后再断开 p 与 s 的链接，令 p 指向 s 之后的结点，再释放空间即可
若删除的是最后结点，由于其没有后继结点，无法采用上述方法，只能从头到尾开始遍历，在单链表中匹配与 p 地址相同的结点，然后将该结点前的结点指向 NULL，再释放空间

可见，若删除的是非最后结点，时间复杂度为 $O(1)$；若删除的是最后结点，时间复杂度为 $O(n)$

无论是带头结点的单链表，还是不带头结点的单链表，在该删除指定结点方法中，操作是一致的，唯一的区别仅是：当删除的是最后结点时，需要从头到尾开始遍历，带头结点的单链表，从头结点的下一结点开始，不带头结点的单链表，从头指针指向的结点开始

对于带头结点的单链表 L，在删除指定结点时，若删除的是非最后结点，直接进行删除即可，若删除的是最后一个结点，则从头结点的下一结点开始遍历

template <typename T>
bool LinkList<T>::deleteNodeByLocate(LNode<T> *p, T &elem) { //删除指定结点p
    if (p == NULL)
        return false;
    
    //删除非最后一个结点
    if (p->next != NULL) {
        LNode<T> *s = p->next; //指向结点p的下一结点s
        elem = p->data;        //记录数据域，通过引用的方式返回
        p->data = s->data;     //将结点p的下一结点s中的数据存到结点p中
        p->next = s->next;     //断开结点p与其下一结点s的链接关系
        free(s);               //释放p的下一结点的空间
        return true;
    }

    //删除最后一个结点
    if (p->next == NULL) {
        LNode<T> *s = first->next; //指向头结点的临时指针
        while (s->next != NULL) {  //从头结点所指向的结点开始遍历
            if (s->next == p) {    //地址相同，即找到链表的最后一个结点
                elem = p->data;    //记录数据域，通过引用的方式返回
                s->next = NULL;    //断开链接关系
                free(p);           //释放p的空间

                return true;
            }
            s = s->next;
        }
    }
}

对于不带头结点的单链表 L，在删除指定结点时，若删除的是非最后结点，直接进行删除即可，若删除的是最后一个结点，则从头指针所指向的结点开始遍历

template <typename T>
bool LinkList<T>::deleteNodeByLocate(LNode<T> *p, T &elem) { //删除指定结点p
    if (p == NULL)
        return false;
    
    //删除非最后一个结点
    if (p->next != NULL) {
        LNode<T> *s = p->next; //指向结点p的下一结点s
        elem = p->data;        //记录数据域，通过引用的方式返回
        p->data = s->data;     //将结点p的下一结点s中的数据存到结点p中
        p->next = s->next;     //断开结点p与其下一结点s的链接关系
        free(s);               //释放p的下一结点的空间
        return true;
    }

    //删除最后一个结点
    if (p->next == NULL) {
        LNode<T> *s = first;       //指向头指针所指向的结点的临时指针
        while (s->next != NULL) {  //从头指针所指向的结点开始遍历
            if (s->next == p) {    //地址相同，即找到链表的最后一个结点
                elem = p->data;    //记录数据域，通过引用的方式返回
                s->next = NULL;    //断开链接关系
                free(p);           //释放p的空间

                return true;
            }
            s = s->next;
        }
    }
}

删除给定值的所有结点

对于给定值 elem，要在单链表中删除所有数据域为 elem 的结点，删除方法如下：

设置一个指向工作结点 p 的前驱结点的指针 pre
用工作结点 p 从头到尾扫描单链表：若 p 所指结点值为 elem，则将其删除，并让 p 指向下一结点，否则令 pre 与 p 后移一个结点

对于带头结点的单链表 L，前驱指针一开始设为头结点 first，工作指针设为头指针指向的下一结点 first->next，在删除给定值的所有结点时，从头结点的下一结点开始遍历

template <typename T>
bool LinkList<T>::deleteNodeByElem(T elem) { //删除所有值为elem的结点
    LNode<T> *pre = first;                   //前驱指针
    LNode<T> *p = first->next;               //从头结点的下一结点开始
    if (p == NULL)
        return false;
    while (p != NULL) {
        if (p->data == elem) { //值相同
            LNode<T> *s = p;   //暂存工作指针p所指向的结点
            p = p->next;       //工作指针p指向下一结点
            pre->next = p;     // p的前驱结点指向p
            free(s);           //释放要删除的结点
        } else {               //值不同
            pre = p;           //前驱指针pre后移
            p = p->next;       //工作指针p后移
        }
    }
}

对于不带头结点的单链表 L，在删除给定值的所有结点时，前驱指针一开始设为 NULL，工作指针设为头指针指向的结点 first，在删除给定值的所有结点时，从头指针指向的结点开始遍历

template <typename T>
bool LinkList<T>::deleteNodeByElem(T elem) { //删除所有值为elem的结点
    LNode<T> *pre = NULL;                    //前驱指针
    LNode<T> *p = first;                     //从头指针指向的结点开始
    if (p == NULL)
        return false;
    while (p != NULL) { 
        if (p->data == elem) { //值相同
            LNode<T> *s = p;   //暂存工作指针p所指向的结点
            p = p->next;       //工作指针p指向下一结点
            pre->next = p;     //p的前驱结点指向p
            free(s);           //释放要删除的结点
        } else {               //值不同
            pre = p;           //前驱指针pre后移
            p = p->next;       //工作指针p后移
        }
    }
}

【头插法与尾插法】

头插法

头插法，是每次将新申请的结点插入到链表最开始的位置，举例来说，对于一个序列 $\{1,2,3,4,5\}$，在使用头插法建立单链表后，单链表从头到尾每个结点的数据域依次为 $\{5,4,3,2,1\}$，因此，其常用于链表的建立、链表的逆置

可以发现，对于带头结点的单链表来说，每次插入都是对头结点进行后插操作

template <typename T> 
void LinkList<T>::headInsert(T data[], int len) { //头插法
    for (int i = 0; i < len; i++)                 //每一次对头结点进行后插操作
        insertNextNode(first, data[i]);
}

对于不带头结点的单链表来说，其实质是建立后继关系，通过不断交换头指针与新结点的地址来实现头插

template <typename T> 
void LinkList<T>::headInsert(T data[], int len) { //头插法
    for (int i = 0; i < len; i++) {
        LNode<T> *p = (LNode<T> *)malloc(sizeof(LNode<T>));
        p->data = data[i]; //填充数据域
        p->next = first;   //将新结点指向头指针所指向的地址
        first = p;         //更改头指针地址为新结点地址
    }
}

尾插法

尾插法，是每次将新申请的结点插到链表的最后面，由于指针机制是后向机制，每次插入都需要从头指针开始遍历到表尾，为减少时间复杂度，尾插法引入了尾指针 tail，其指向单链表的表尾结点，使得每次插入都能让新结点处于最后的位置

对于带头结点的单链表来说，只需要利用尾指针 tail，不断地申请新结点，填充数据域后建立后继关系即可

template <typename T> 
void LinkList<T>::tailInsert(T data[], int len) { //尾插法
    LNode<T> *tail = first;                       //尾指针
    for (int i = 0; i < len; i++) {
        LNode<T> *p = (LNode<T> *)malloc(sizeof(LNode<T>)); //申请新结点
        p->data = data[i];                                  //填充数据域

        tail->next = p; //建立后继关系
        tail = p;       //更改尾指针为新结点p地址
    }
    tail->next = NULL; //建立完毕，尾指针指针域置空
}

对于不带头结点的单链表来说，由于初始头指针指向为空，因此要先建立一个初始结点，将头指针指向该结点，再对剩下的 n-1 个元素建立结点，填充数据域建立后继关系

template <typename T> 
void LinkList<T>::tailInsert(T data[], int len) { //尾插法
    LNode<T> *tail = first;                       //尾指针
    
    //初始结点
    LNode<T> *p = (LNode<T> *)malloc(sizeof(LNode<T>)); 
    p->data = data[0];  //初始结点数据域
    p->next = first;    //初始结点指向头指针
    first = p;          //更改头指针地址为初始结点地址
    tail = first;       //更改尾指针地址为头指针地址，即初始结点地址

    //初始结点后的len-1个结点
    for (int i = 1; i < len; i++) {
        LNode<T> *p = (LNode<T> *)malloc(sizeof(LNode<T>)); //申请新结点
        p->data = data[i];                                  //填充数据域

        tail->next = p; //建立后继关系
        tail = p;       //更改尾指针为新结点p地址
    }
    tail->next = NULL;  //建立完毕，尾指针指针域置空
}