【概述】

分块索引，又称索引顺序查找，其吸取了顺序查找和二分查找的优点，属于线性索引结构，既适用于静态索引，又适用于动态索引

其基本思想是将查找表分为若干子块，这些子块之间满足分块有序这个要求，即这些块满足以下两个条件：

块间有序：后一块的所有记录的关键字要大于前一块的所有记录的关键字
块内无序：每一块的记录不要求有序

【结构】

对于分块有序的数据集，将每块对应一个索引项，其结构分为以下三个部分：

最大关键码：存储每一块的最大关键字，以便在下一块中的最小关键字也能比这一块的最大关键字大
块长：存储块中记录个数
块首地址：指向块首数据元素的指针

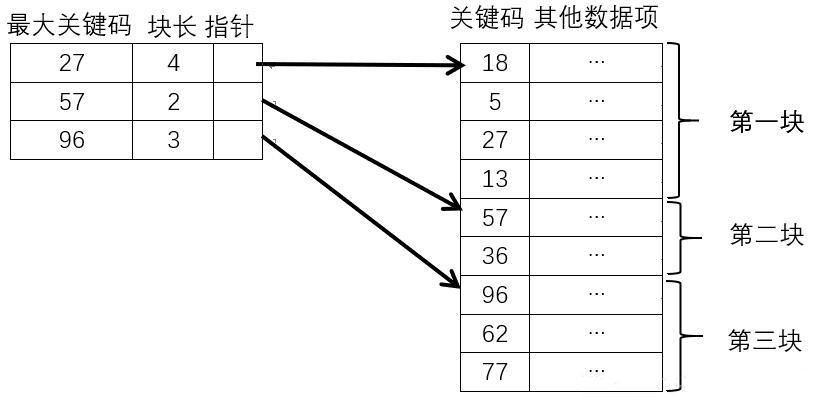
【查找过程】

在分块表中进行查找，整个过程分为两步：

在整个索引表中，通过顺序查找或二分查找，来确定待查记录所在的块
在确定的相应块中，采用顺序查找，查找待查关键字

如上图，关键码集合为 $\{18,5,27,13,57,36,96,62,77\}$，按照关键码值 $27,57,96$ 分为三个块，从而形成图中左边的索引表

假设查找待查元素为 $5$，那么会先在索引表中对元素 $5$ 进行查找，确定其所在的块是第一块，然后在第一块的四个元素 $18,5,27,13$ 中进行查找

【平均查找长度】

分块索引的平均查找长度为索引查找和块内查找的平均长度之和

假设索引查找和块内查找的平均查找长度分别为 $L_I,L_S$，那么分块索引的平均查找长度为：

$ASL=L_I+L_S$

对于含有 $n$ 个记录的文件，假设将其分为 $m$ 个块，每块中有 $t$ 条记录，即：

$n=m*t$

在等概率的情况下，若在索引表和块内中均采用顺序查找，则平均查找长度为：

$\begin{align} ASL &= L_I+L_S \notag \\ &= \frac{m+1}{2}+\frac{t+1}{2} \notag \\ &= \frac{1}{2}(\frac{n}{t}+1)+1 \notag \\ &= \frac{t^2+2t+n}{2t} \notag \end{align}$

可以发现，平均查找长度不仅取决于数据集的总记录数 $n$，还取决于每一个块中的记录条数 $t$

最佳的情况就是分的块数 $m$ 与块中记录数相同，即：$n=mt=tt$，有：$t=\sqrt n$，此时，平均查找长度取最小值：

$ASL=\sqrt n +1$

若在索引表和块内中均采用顺序查找，则平均查找长度为：

$\begin{align} ASL &= L_I+L_S \notag \\ &= \lceil \log_2 (m+1) \rceil + \frac{t+1}{2} \notag \\ \end{align}$

【实现】

假设分块长度为 $\sqrt n$，那么分块的实现如下：

int block;  //block为块的长度
int sum;    //sum为块的个数
int a[N];   //存放数列元素
int pos[N]; //tag为操作标记
int tag[N]; //pos记录第i个元素在第几个块中
void init(int n) { //初始化
    block = (int)sqrt(n); //块的长度
    sum = n / block; //块数
    if (n % block)
        sum++;
    for (int i = 1; i <= n; i++) //第i个元素在第几块中
        pos[i] = (i - 1) / block + 1;
}