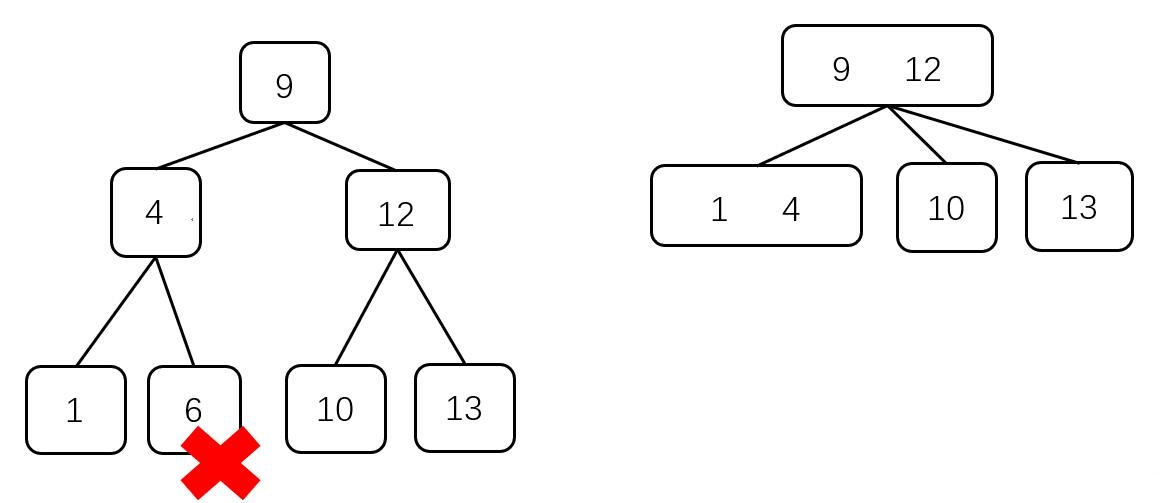
【结构】
2-3 树(2-3 Tree),是一种多路查找树,其是一棵具有如下特性的树:
- 每个结点都具有 $2$ 个孩子或 $3$ 个孩子,具有 $2$ 个孩子的结点称为 $2$ 结点,具有 $3$ 个孩子的结点称为 $3$ 结点
- $2$ 结点包含 $1$ 个关键码,且其具有 $2$ 个孩子,同时,左子树包含小于 $2$ 结点的元素,右子树包含大于 $2$ 结点的元素
- $3$ 结点包含一大一小 $2$ 个关键码,且其具有 $3$ 个孩子,同时,左子树包含小于 $3$ 结点两个关键码的元素,右子树包含大于 $3$ 结点两个关键码的元素,中间子树包含介于 $3$ 结点两个关键码之间的元素
- 所有叶结点都在同一层
当所有叶结点均处于同一层时,就说这棵树是树高平衡的,可见,2-3 树是树高平衡的,其最大的优点正是能够以相对较低的代价来保持树高平衡
如下图,内部结点 $12$、$48$ 为 $2$ 结点,内部结点 $\{18,33\}$、$\{23,30\}$ 为 $3$ 结点
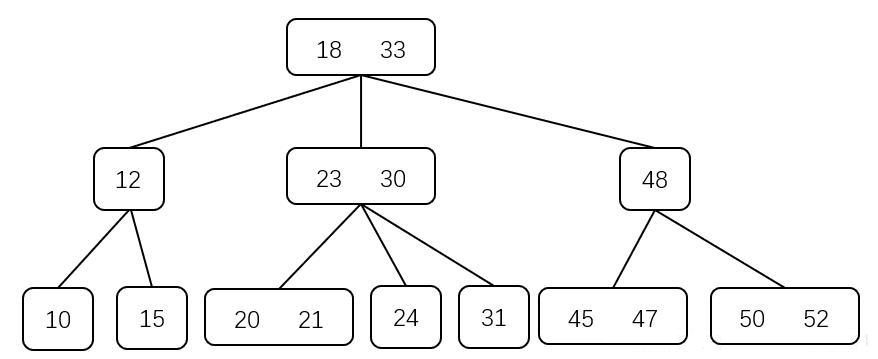
同时,可以发现:
- 对于一棵高度为 $h$ 的 2-3 树,其至少有 $2^{h-1}$ 个叶结点,此时每个分支结点都有 $2$ 个孩子,从而形成一棵满二叉树
- 对于一棵高度为 $h$ 的 2-3 树,其至多有 $3^{h-1}$ 个叶结点,此时每个分支结点都有 $3$ 个孩子,从而形成一棵满三叉树
【查找】
在 2-3 树中,查找一个关键码的过程类似于在二叉排序树中的查找
在 2-3 树中查找给定 $k$ 值的过程是:
- 若
root是空树,查找失败 - 若
k = root->data,查找成功 - 对于 $2$ 结点,若
k < root->data,则在root的左子树进行查找;若k > root->data,则在root的右子树进行查找 - 对于 $3$ 结点,若
k < root->smallData,则在root的左子树进行查找;若k > root->bigData,则在root的右子树进行查找;否则,在root的中间子树进行查找
上述过程一直持续到 $k$ 被找到或者待查找的子树为空,若待查找的子树为空,则查找失败
值得注意的是,当查找失败时,恰好找到了以 $k$ 为键值的新结点在 2-3 树中的插入位置
以下图为例,要如果查找 $24$,首先查找根结点,由于 $24$ 大于根结点的 smallData=18,小于 bigData=33,那么进入第二层的中间子树查找;在第二层中,由于 $24$ 大于 smallData=23,小于 bigData=30,进入第三层的中间子树查找,最终到达包含 $24$ 的结点

【插入】
在 2-3 树中,插入一个关键码的过程类似于在二叉排序树中的插入
插入一个记录的过程如下:
1.找到要被插入记录应该被插入的叶结点
2.若该叶结点为一个 $2$ 结点,那么可以直接将该记录添加在该叶结点中,从而升级为 $3$ 结点
3.若该叶结点为一个 $3$ 结点,那么需要将该结点进行分裂-提升,拆分为两个 $2$ 结点,再向上提升,具体步骤如下:
1)设要插入的叶结点为 $L$,分裂一个新结点 $L’$
2)结点 $L$ 得到 $3$ 结点中两个关键码与新插入的记录中最小的一个,结点 $L’$ 得到最大的一个
3)进行一次提升,即将剩余的一个关键码与一个指向 $L’$ 的指针传回父结点,并将被提升的关键码插入父结点
4)若父结点为 $2$ 结点,那么重复步骤 2
5)若父结点为 $3$ 结点,那么重复步骤 3 的分裂-提升过程
如下图,假设在当前 2-3 树中,依次插入记录 $14$、$55$

在插入 $14$ 时,从根结点开始查找,到达存储 $15$ 的叶结点时,发现其是一个 $2$ 结点,直接将 $14$ 插入即可
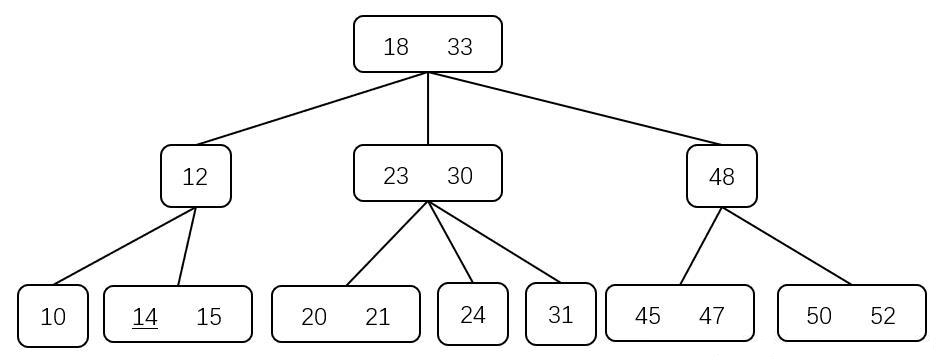
在插入 $55$ 时,从根结点开始查找,到达存储 $\{50,52\}$ 的结点,其是一个 $3$ 结点,需要进行分裂-提升
此时,存储 $\{50,52\}$ 的结点保存 $50$、$52$、$55$ 中最小的 $50$,新分裂的结点保存最大的 $55$,剩余的 $52$ 向上提升,发现其存储 $48$ 的结点为 $2$ 结点,直接将 $52$ 插入
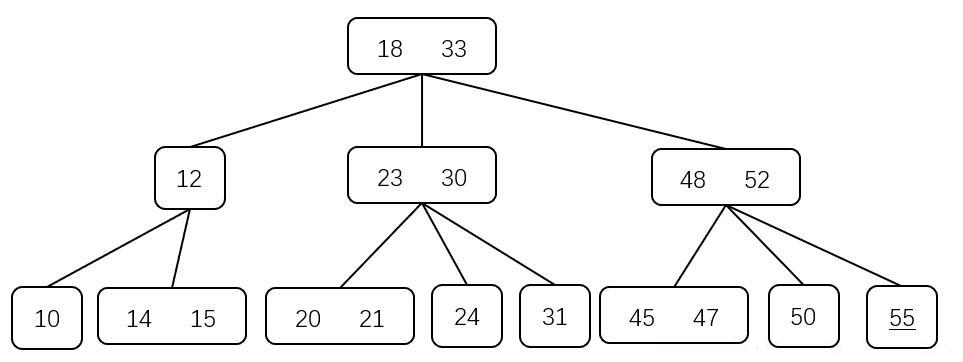
【删除】
当从 2-3 树删除一个关键码时,有三种情况要考虑:
1.从内部结点删除记录
当所删除的关键码为内部结点时,对树进行中序遍历,将要删除的关键码的中序前驱或中序后继元素作为替代元素即可

2.从叶结点为 $3$ 结点删除记录
当所删除的关键码位于叶结点且该结点为 $3$ 结点时,直接在该结点删除该关键码即可,不会影响整棵树的结构
3.从叶结点为 $2$ 结点删除记录
当所删除的关键码位于叶结点且该结点为 $2$ 结点时,可分为四种情况进行讨论
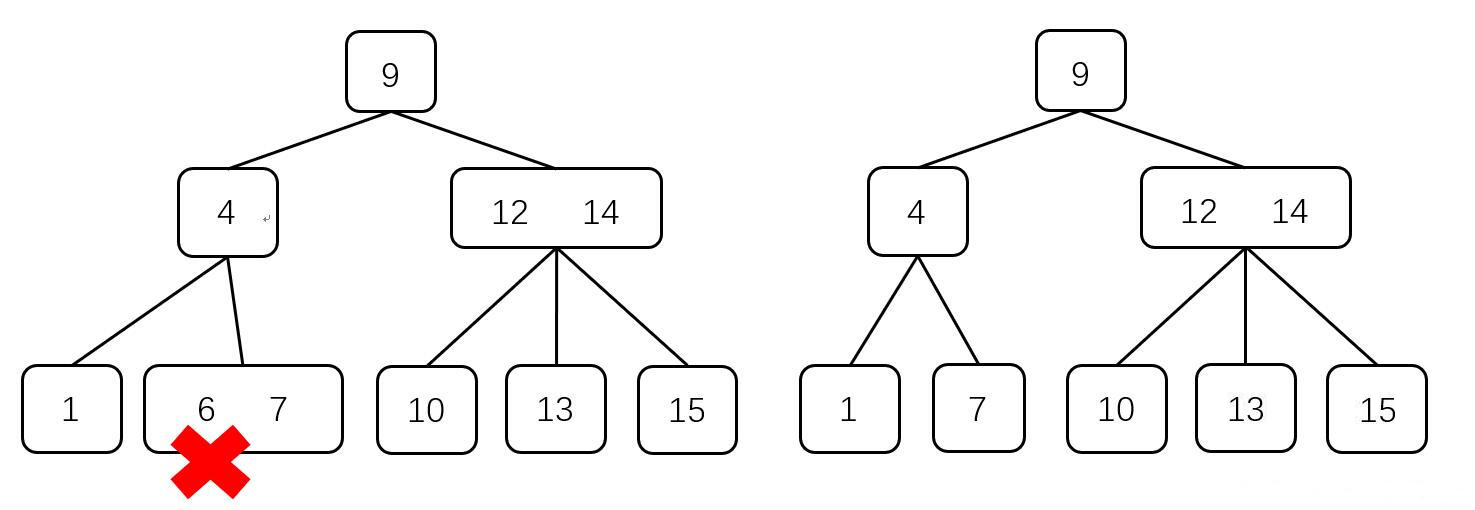
1)$2$ 结点的父结点是 $3$ 结点
此时,将 $3$ 结点进行拆分,根据删除要删除的元素的大小,将被拆分的点与 $3$ 结点的子树进行合并
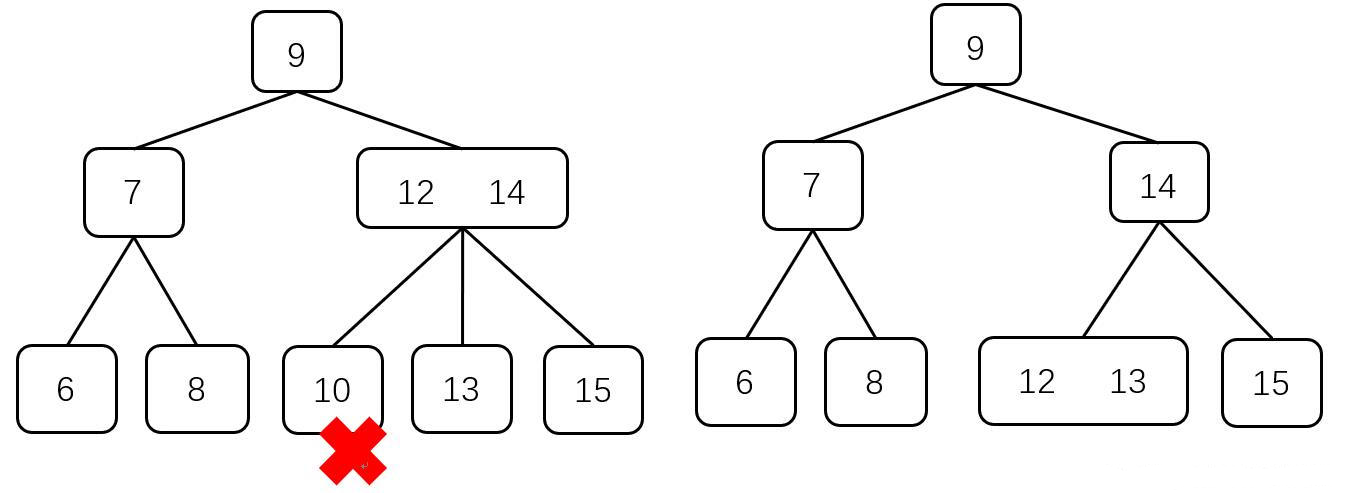
2)$2$ 结点的父结点是 $2$ 结点,且拥有一个 $3$ 结点的右孩子
此时,将父结点与右孩子一起进行左旋,令父结点的右孩子的较小值成为新的父结点,原先的父结点成为新的左孩子,原先的右孩子的较大值不做改变
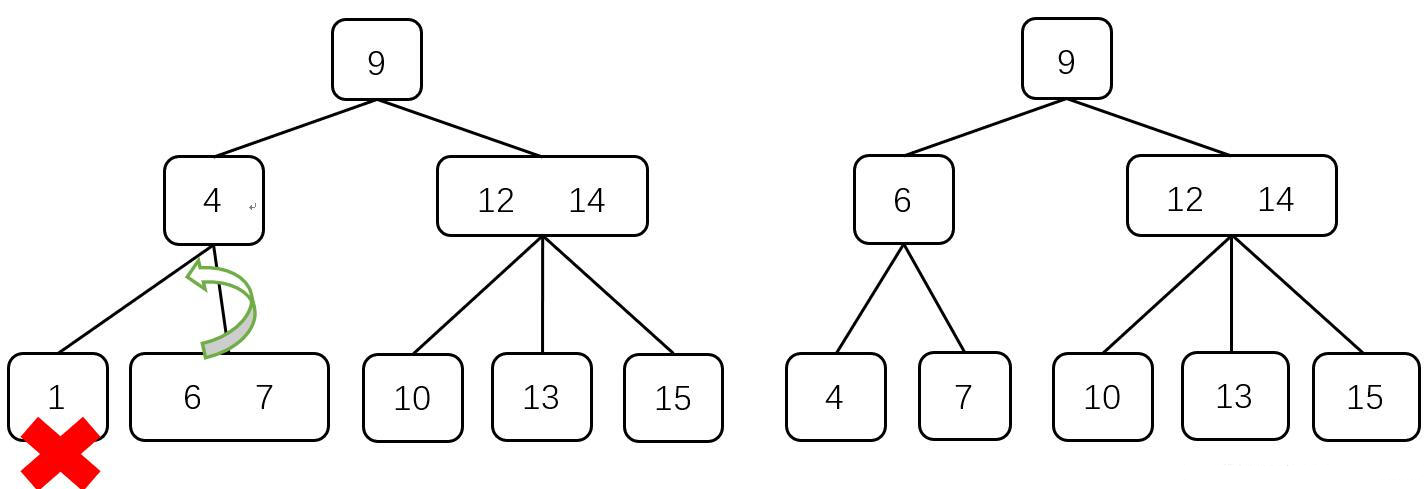
3)$2$ 结点的父结点是 $2$ 结点,且拥有一个 $2$ 结点的右孩子
此时,在不破坏 2-3 树的性质的前提下,将 $2$ 结点的右孩子变为 $3$ 结点的右孩子,然后删除要删除的元素,并将剩下的三个点进行左旋调整
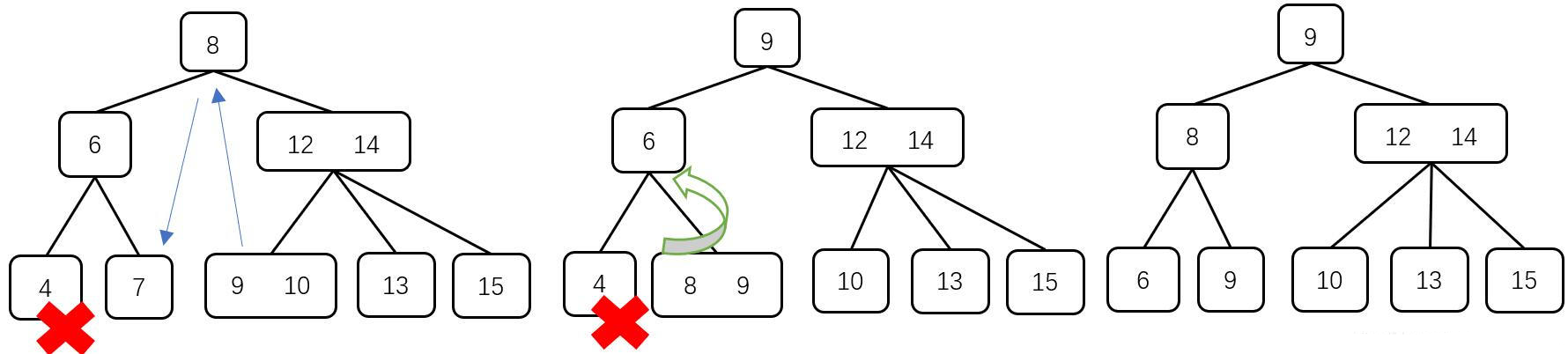
4)当前树是一个满二叉树
此时,删除任意一个结点都会破坏 2-3 树的性质,需要考虑在不改变 2-3 树的顺序的情况下,将 2-3 树的层次减少一层