【B 树的结构】

定义

B 树（B-Tree），是一种多路平衡查找树，其所有结点的平衡因子为 $0$，主要面向于动态查找，常用于文件系统中

B 树中，结点最大的孩子数目称为 B 树的阶，一棵 $m$ 阶的 B 树或为空树，或为满足以下性质的 $m$ 叉树：

叶结点的父结点称为终端结点，若根结点不是终端结点，则至少有 $2$ 棵子树
每个结点，最多含有 $m-1$ 个关键字，同时最多有 $m$ 棵子树
除根结点外的所有非终端结点，至少含有 $\left \lceil \frac{m}{2} \right \rceil-1$ 个关键字，同时最少有 $\left \lceil \frac{m}{2} \right \rceil$ 棵子树
所有的非终端结点都包括数据：$\{n,P_0,K_1,P_1,K_2,…,K_n,P_n\}$，其中，$n$ 为结点中关键码个数，且满足 $\left \lceil \frac{m}{2} \right \rceil-1\leq n\leq m-1$ ，$K_i$ 为关键码，$P_i$ 为指向子树根结点的指针，且指针 $P_i$ 所指子树中所有结点的关键码均小于 $K_{i+1}$ 大于 $K_i$
所有的叶结点均在同一层，且不带任何信息，这些结点实质上并不存在，指向这些结点的指针为空

可见，2-3 树，就是一棵 $3$ 阶 B 树

性质

$B$ 树具有如下性质：

结点的孩子个数为关键字个数加 $1$
若根结点没有关键字，则没有子树，此时 $B$ 树为空
若根结点有关键字，则子树必然大于等于 $2$ 棵，即子树个数为关键字个数加 $1$
除根结点外的所有非终端结点，最少有 $\left \lceil \frac{m}{2} \right \rceil-1$ 个关键字 ，最多有 $m-1$ 个关键字
除根结点外的所有非终端结点，最少有 $\left \lceil \frac{m}{2} \right \rceil$ 棵子树，最多有 $ m $ 棵子树，
结点中关键字从左到右递增有序，关键字两侧均有指向子树的指针，左边指针所指子树的所有关键字均小于该关键字，右边指针所指子树的关键字均大于该关键字
下层结点关键字总是落在由上层结点关键字所划分的区间内
所有叶结点均在最后一层，代表查询失败的位置

实例

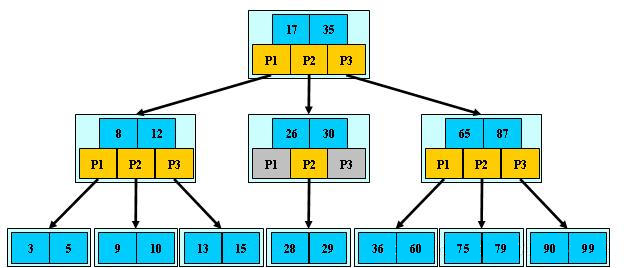
如下图，是一个 $3$ 阶 B 树，除根结点外的非终端结点，最少有 $\left \lceil \frac{m}{2} \right \rceil=\left \lceil \frac{3}{2} \right \rceil=2$ 棵子树，最多有 $3$ 棵子树，同时，最少有 $\left \lceil \frac{m}{2} \right \rceil-1=2-1=1$ 个关键字，最多有 $2$ 个关键字

由于下层结点关键字总是落在由上层结点关键字所划分的区间内，以第二层最左结点为例，其关键字为 $\{8,12\}$，划分为 $3$ 个区间 $(- \infty,8)$、$(8,12)$、$(12,17)$，该结点的 $3$ 个指针 $\{p_1,p_2,p_3\}$ 所指子树的关键字，均落在这 $3$ 个区间内

【B 树的高度】

对于任意一棵包含 $n$ 个关键字，高度为 $h$，阶数为 $m$ 的 B 树，其高度满足如下约束：

1） $h$ 的下界

每个结点最多有 $m$ 棵子树时，有 $m-1$ 个关键字

假设在一棵 $m$ 阶 B 树在高度为 $h$ 时高度最小，那么关键字个数应满足：

$n\leq (m-1)(1+m+m^2+...+m^{h-1})=m^h-1$

故可得高度 $h$ 的下界为：

$h\geq log_m(n+1)$

2）$h$ 的上界

每个结点中的关键字个数达到最少时，容纳同样多的关键字的 B 树高度最大

根据 B 树的定义：第一层至少有 $1$ 个结点，除根结点外的每个非终端结点至少有 $\left \lceil \frac{m}{2} \right \rceil$ 棵子树

故而，第二层至少有 $2$ 个结点，第三层至少有 $2\left \lceil \frac{m}{2} \right \rceil$ 个结点，以此类推，第 $h+1$ 层至少有 $2(\left \lceil \frac{m}{2} \right \rceil)^{h-1}$ 个结点

由于 $B$ 树的高度不包含最后一层不带任何信息的叶结点层，即不包含第 $h+1$ 层，那么对于关键字为 $n$ 的 $B$ 树，叶结点即查找不成功的结点数为 $n+1$，那么有：

$n+1 \geq 2(\left \lceil \frac{m}{2} \right \rceil)^{h-1}$

故可得高度 $h$ 的上界为：

$h\leq log_{\left \lceil \frac{m}{2} \right \rceil}(\frac{n+1}{2}+1)$

3）$h$ 的范围

综上所述，高度 $h$ 满足：

$log_m(n+1)\leq h \leq log_{\left \lceil \frac{m}{2} \right \rceil}(\frac{n+1}{2})+1$

假设一棵 $3$ 阶 B 树有 $8$ 个关键字，那么高度范围为：

$log_3(8+1)\leq h\leq log_{\left \lceil \frac{3}{2} \right \rceil}(\frac{8+1}{2})+1$

即：$2\leq h \leq 3.17$

4）关键字与结点

对于一个高度为 $h$ 的 $m$ 阶 B 树，根结点外的所有非终端结点至少有 $\left \lceil \frac{m}{2} \right \rceil$ 棵子树，最多有 $m$ 棵子树

记 $k=\left \lceil \frac{m}{2} \right \rceil$，那么在最少的情况时，有：

第 $1$ 层：最少有 $1$ 个结点，最少有 $1$ 个关键字
第 $i$ 层：最少有 $2k^{h-2}$ 个结点，最少有 $2k^{h-i}(k-1)$ 个关键字

故而，$h$ 层的 $m$ 阶 B 树，最少包含 $1+2(k^{h-1}-1)$ 个关键字，最少含有 $2^h-1$ 个结点

同理，在在最多的情况时，有：

第 $1$ 层：最多有 $1$ 个结点，最多有 $1$ 个关键字
第 $i$ 层，最多有 $m^{i-1}$ 个结点，最多有 $(m-1)m^{i-1}$ 个关键字

故而，$h$ 层的 $m$ 阶 B 树，最多包含 $m^h-1$ 个关键字，最多含有 $\frac{1-m^h}{1-m}$ 个结点

【B 树的查找】

B 树的查找与二叉查找树相似，只是每个结点都是多个关键字的有序表，在每个结点上所做的不是二路分支决定，而是根据该节点的子树所做的多路分支决定

B 树的查找包含两个基本操作：

在 B 树中找结点（在磁盘中进行）
在结点中找关键字（在内存中进行）

B 树一般存储于磁盘中，因此在找到目标结点后，先将结点信息读入内存，然后在结点中采用顺序查找的方法寻找关键字，查找到叶结点时，对应指针为空指针，说明树中没有对应关键字，查找失败

以下图为例，假设要查找关键字 $79$

根结点有两个关键字 $\{17,35\}$，$79>35$，若关键字 $79$ 存在，必在根结点的右子树里
右子树有两个关键字 $\{65,87\}$，$65<79<87$，若关键字 $79$ 存在，必在该结点的中子树里
中子树有两个关键字 $\{75,79\}$，查找到关键字 $79$，查找成功

【B 树的插入】

过程

将关键字 $key$ 插入 B 树的过程如下：

定位：利用 B 树查找算法，找出插入该关键字的最低层中的某个非叶结点
插入：每个非失败结点的关键字个数都在区间 $[\left \lceil \frac{m}{2} \right \rceil-1,m-1]$ 内
- 若插入后的结点关键字小于 $m$，直接插入
- 若插入后的结点关键字大于 $m-1$，对结点进行分裂
分裂：取一个新结点，在插入 $key$ 后的原结点，从中间位置 $\left \lceil \frac{m}{2} \right \rceil$，将关键字分为两部分
- 左部分包含的关键字放在原结点中
- 右部分包含的关键字放在新结点中
- 中间位置的结点插入原结点的父结点
提升：若分裂过程中，中间位置的结点插入父结点，使得父结点中关键字个数也达到上限，那么继续进行分裂操作，直到这个过程传达到根结点为止，此时，$B$ 树高度 $+1$

实例

如下图，给出一的 $3$ 阶 B 树，现要在其中依次插入 $14$、$55$

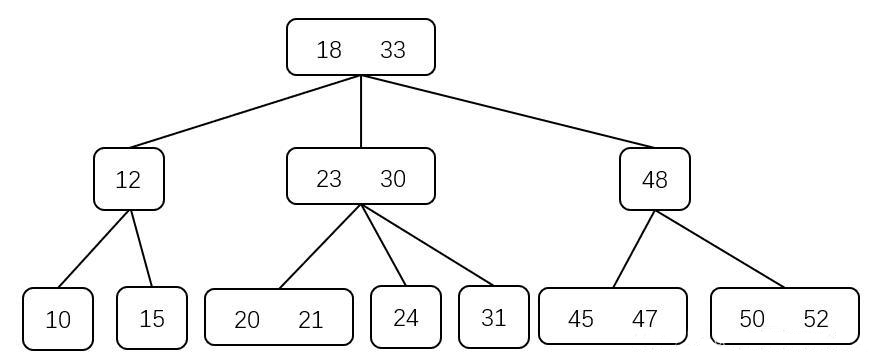
在插入 $14$ 时，从根结点开始查找，到达存储 $15$ 的叶结点，其是一个 $2$ 结点，直接将 $14$ 插入即可

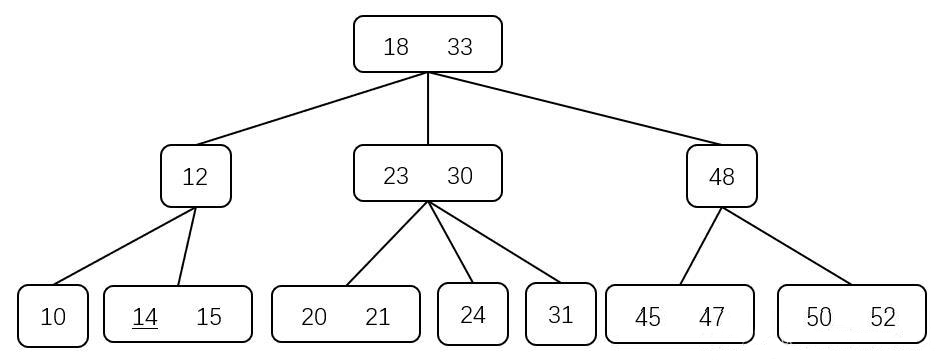
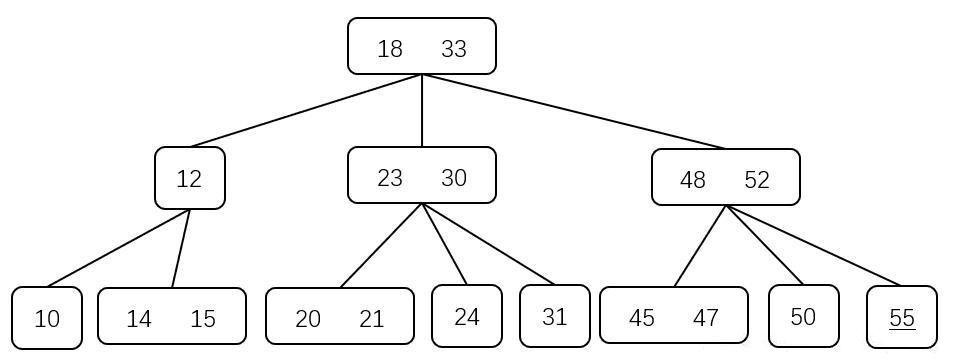
在插入 $55$ 时，从根结点开始查找，到达存储 $\{50,52\}$ 的结点，其是关键字个数为 $2$ ，需要进行分裂，加入 $55$ 后，三个关键码的值为 $\{50,52,55\}$，其中，令中值 $52$ 提升，小值 $50$ 与大值 $55$ 作为父结点的叶结点

【B 树的删除】

B 树的删除要保证删除后的结点中的关键字个数大于等于 $\left \lceil \frac{m}{2} \right \rceil-1$

被删关键字 $key$ 可能在终端结点中，也可能不在终端结点中，由此，B 树的删除可分为以下两种情况：

1）不在终端结点

使用 $key$ 的前驱或后继 $key’$ 来代替 $key$，然后在相应结点中删除 $key’$，关键字 $key’$ 必定落在某个终端结点中，这就转换成了删除关键字在终端结点的情况

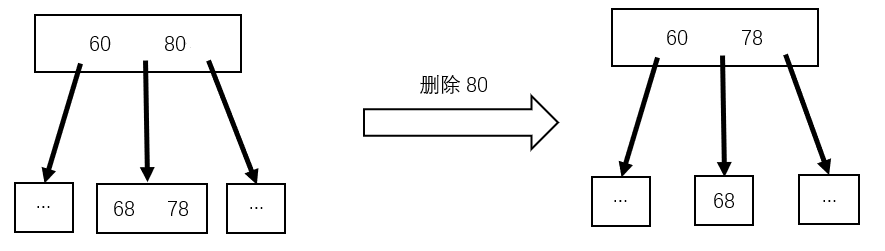
如下图的 $4$ 阶 B 树，删除关键字 $80$，用其前驱 $78$ 替代 $80$，然后在终端结点中，将 $78$ 删除

2）在终端结点

当被删结点在终端结点中，有三种情况：

①直接删除

若被删关键字所在结点的关键字个数 $\geq \left \lceil \frac{m}{2} \right \rceil$，直接删除该关键字后仍满足 B 树定义

②兄弟够借

若被删关键字所在结点的关键字个数 $= \left \lceil \frac{m}{2} \right \rceil-1$，且与该结点相邻的左兄弟或右兄弟结点的关键字个数 $\geq \left \lceil \frac{m}{2} \right \rceil$，将该结点、左兄弟或右兄弟结点、父结点中的关键字进行换位，以达到新的平衡

如下图的 $4$ 阶 $B$ 树，删除关键字 $65$，其结点关键字个数 $=\left \lceil \frac{m}{2} \right \rceil-1=1$，右兄弟关键字个数为 $2 \geq \left \lceil \frac{m}{2} \right \rceil = 2$，需要调整结点，用 $71$ 取代原 $65$ 位置，用 $74$ 取代原 $71$ 位置

③兄弟不够借

若被删关键字所在结点的关键字个数 $= \left \lceil \frac{m}{2} \right \rceil-1$，且与该结点相邻的左兄弟或右兄弟结点的关键字个数 $= \left \lceil \frac{m}{2} \right \rceil-1$，则进行合并操作

在合并过程中，父结点中的关键字个数会 $-1$

若父结点是根结点，且关键字个数减少到 $0$，则直接删除根结点，合并后的新结点为根
若父结点不是根结点，且关键字个数减少到 $\left \lceil \frac{m}{2} \right \rceil-2$，则要将其与其兄弟结点进行调整或合并，重复上述步骤，直到符合 $B$ 树要求为止

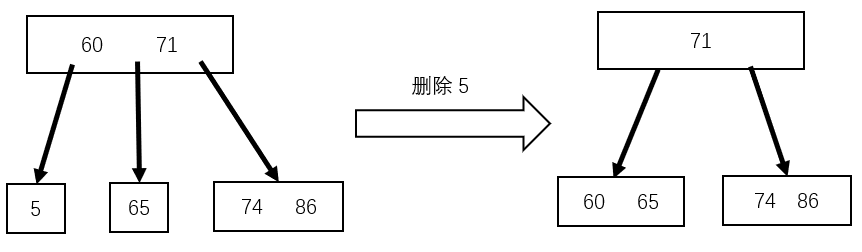
如下图的 $4$ 阶 $B$ 树，删除关键字 $5$，其结点关键字个数 $=\left \lceil \frac{m}{2} \right \rceil-1=1$，右兄弟结点关键字个数 $=\left \lceil \frac{m}{2} \right \rceil-1=1$，在将 $5$ 删除后，将 $60$ 合并到 $65$ 中

【应用】

在实际应用中，B 树常用于文件系统中，且常使得阶数与磁盘存储的页面大小匹配，即一个索引结点大小应取不超过磁盘页块的大小

假设 $B$ 树为 $m$ 阶，那么一个结点最多存放：

$m-1$ 个关键字和对应记录地址（指针）
$m$ 个子树指针
$1$ 个指示结点中的实际关键字个数的整数

假设磁盘页块大小为 $4000B$，指示磁盘地址的指针需要 $5B$，现有 $2*10^7$ 个记录构成的文件，每个记录为 $200B$，其中包括关键字 $5B$，若采用 $B$ 树作索引，$B$ 的阶数为多少？假定文件数据部分未按关键字排序，索引部分要占用多少磁盘页块？

假设为 $m$ 阶 $B$ 树，那么一个结点最多存放：

$m-1$ 个关键字和对应记录地址（指针）
$m$ 个子树指针
$1$ 个指示结点中的实际关键字个数的整数

由题意：

一个结点最多存放 $m-1$ 个关键字，那么关键字所占空间为 $5B\times(m-1)$，相应的对应记录地址亦为 $5B\times(m-1)$
总共需要 $m$ 个子树指针，那么指针所占空间为 $5B\times m$
$1$ 个指示实际关键字个数的整数，取 $int$ 型，为 $2B$

综上，一个结点所占空间满足：

$5B\times(m-1)\times 2+5B\times m+2\leq 4000B$

可得：$m\leq 267$

那么，一个索引结点最多可以存放 $m-1=266$ 个索引项，最少可以存放 $\left \lceil \frac{m}{2} \right \rceil-1=133$ 个索引项

共有 $2\times 10^7$ 个记录，每记录占用 $200B$，每页块可以存放 $\frac{4000}{200}=20$ 个记录，则共需 $\frac{2\times 10^7}{20}=2\times 10^6$ 个页块

最多占用 $\left \lceil \frac{2\times 10^6}{133} \right \rceil=7591$ 个磁盘块作为 $B$ 树索引，最少占用 $\left \lceil \frac{2\times 10^6}{266} \right \rceil=3760$ 个磁盘块作为 $B$ 树索引