【B+ 树】

结构

B+ 树是 B 树的变形树，严格意义上来讲，其已经不是一棵树了，其常用于数据库中

在 B 树中，每一元素在该树中只出现一次，有可能在终端结点上，也有可能在分支结点上，而在 B+ 树中，出现在分支结点中的元素会被当作他们在该分支结点位置的中序后继者中再次列出，此外，每一叶结点都会保存一个指向后一叶结点的指针

一棵 $m$ 阶的 B+ 树满足以下条件：

每个分支结点最多有 $m$ 棵子树
非叶根结点至少有 $2$ 棵子树，其他每个分支结点至少有 $\left \lceil \frac{m}{2} \right \rceil$ 棵子树
结点的子树个数与关键字相等
所有叶结点包含全部关键字及指向相应记录的指针，叶结点中将关键字按大小顺序排序，且相邻叶结点按大小顺序相互链接
所有分支结点中仅包含其各个子结点中关键字的最大值及指向其子结点的指针

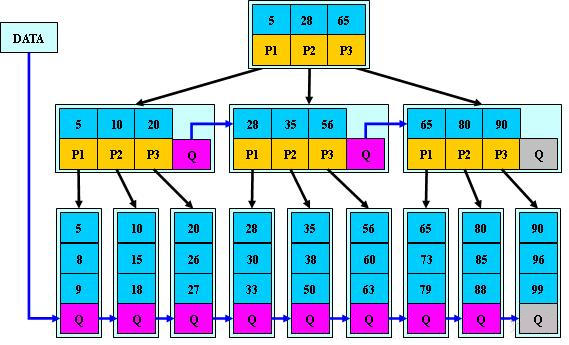
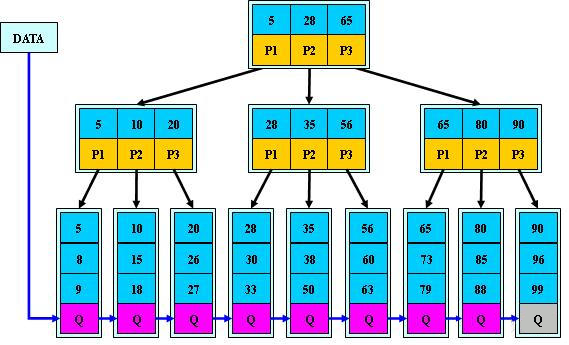
如下图，是一个 $3$ 阶 B+ 树，可以看出，分支结点的某个关键字是其子树中最大关键字的副本，且整个 B+ 树具有两个指针：

值得注意的是，只要是随机查找，就从根结点出发，但在分支结点中找到了待查找的关键字，其也只是用于索引，不能提供实际记录的访问，仍需到达包含此关键字的终端结点

一棵 $m$ 阶的具有 $n$ 个关键字的 B 与 B+ 树的差异在于：

	B 树	B+ 树
子树个数	$n+1 $棵	$n$ 棵
根结点关键字个数范围	$1\leq n\leq m-1$	$1\leq n\leq m$
非根结点关键字个数范围	$\left \lceil \frac{m}{2} \right \rceil -1 \leq n\leq m-1$	$\left \lceil \frac{m}{2} \right \rceil\leq n\leq m$
终端结点	终端结点关键字与其他结点关键字不重复	终端结点关键字与其他结点关键字重复（包含所有关键字）
叶结点	为空，表示查找失败	包含信息，非叶结点仅起索引作用
操作	在非叶结点上进行	在叶结点上进行

B* 树是 B+ 树的变形树，其也非严格意义上的树

B* 树是在 B+ 树的基础上进行了改进，即在 B+ 树的非根和非叶子结点上增加了指向兄弟的指针，且规定非叶结点关键字个数至少为 $\frac{2}{3}m$，即块的最低使用率为 $\frac{2}{3}$（B+ 树只有 $\frac{1}{2}$）

可以看出，B* 树分配结点的概率要比 B+ 树低，空间利用率更高